X射线照在晶体上，将被晶体内各原子中的电子所散射。衍射现象是X射线被晶体散射的一种特殊表现。由于晶体具有周期性结构，散射波中与原射线波长相同的相干散射波相互干涉，在一特定的方向上将互相加强，产生衍射线。晶体产生的衍射方向决定于晶体微观结构的类型（晶胞类型）及其基本尺寸（晶面间距、晶胞参数等）；衍射线的强度决定于晶胞中各组成原子的元素种类及其分布排列坐标。衍射方向和晶体结构间关系的两个方程为劳埃（Laue）方程和布拉格（W.L.Bragg）方程。前者以直线点阵为出发点，后者以平面点阵为出发点，这两个方程式是等效的。
现在讨论布拉格方程：晶体的空间点阵是由一系列平行而等间距的平面点阵（hkl），或称晶面按一定序列堆垛而成。同一晶体不同晶面在空间的取向不同，晶面间距d（hkl）也不相同。设一组晶面族，间距为d（hkl），一束X射线入射到该晶面族上，与晶面的夹角为θ。每个晶面的散射波给出最大干涉强度的条件应该是：入射角和反射角相等，且入射线、反射线和平面法线三者在同一平面内（同镜面对可见光的反射条件一样），如图4-5（a）所示，此时为了保证光程一样。图中入射线在P，Q，R时波前相位相同，而散射线在P′，Q′，R′处仍是相同的，这是产生衍射的必要条件。
如图4-5（b）所示的晶面1，2，3…，间距为d（hkl），相邻两个晶面上的入射X射线和反射线的光程差为：MB＋BN，而
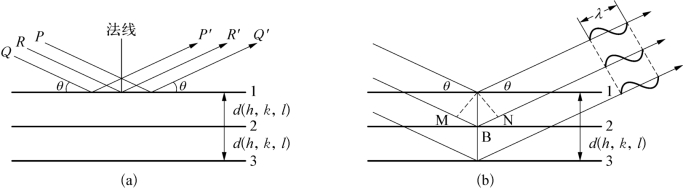
图4-5 原子的X射线反射
（a）一层原子的反射 （b）多层原子的反射
即光程差为2 d（hkl）sinθn。根据衍射条件，只有光程差为波长λ的整数倍时，相干散射波才能互相加强而产生衍射。由此晶面族产生衍射的条件为
上式称为布拉格方程，式中n为1，2，3等整数，λn为相应某一n值的衍射角，n称为衍射级数。布拉格方程是晶体学中最基本的方程之一，只有符合布拉格方程的条件才能发生衍射。根据布拉格方程，晶体衍射实验X射线的波长λ＜2d；但是λ也不能太小，否则衍射角将很小，集中在出射光路附近的很小的角度范围内，使观测无法进行。晶面间距一般在1 nm以内；此外考虑到在空气光路中波长大于0.2 nm的X射线衰减非常严重，所以在晶体衍射中常用到的X射线波长一般在0.05～0.25 nm之间。
关于布拉格方程还需作几点说明：①由于sinθ≤1，只有2d≤λ时才能发生衍射。换言之，在d＞λ／2的晶面上不可能产生衍射线。②对于n级衍射，布拉格方程可以写成2（d／n）sinθ=λ，即第n级衍射也可以在形式上表示是某一晶面族的一级衍射，晶面族与原来的（hkl）晶面平行的间距为d／n。按晶面指数的规定，这些晶面应该是（nh，nk，nl）。例如（120）晶面的n=2的衍射可以看作是（240）晶面的n=1的衍射。利用这种表示方法，布拉格方程可以表示为2d sinθ=λ。
多晶X射线衍射的强度：所谓衍射线的强度是指其“积分强度”。积分强度是一个能量的概念，在理论上能计算出而实验上也能进行测量。在晶体衍射的记录图上，衍射仪记录图的强度曲线下的面积，应该和检测点处衍射线功率成正比。在理论上把检测点处通过单位面积上衍射线的功率定义为某衍射线的强度（绝对积分强度）。纯物质衍射线强度的表达式简单表示为
式中，I0为单位截面上入射单色X射线的功率；|F|称为结构因子，取决于晶体的结构及单个晶胞内所含的原子性质；K是一个综合因子，对于特定的衍射线，它与实验时的衍射几何条件、式样的形状、吸收性质、温度以及一些物理常数有关。
一般金属材料多半是多晶体，它是由许多混乱取向的小晶粒组成，每个小晶粒内部的点阵排列方式是完全相同的。用单一波长（单色）的X射线照射多晶样品时，如果X射线是平行线束，对于某一定指数的晶面族，只有入射角θ满足布拉格方程时，才能产生衍射。对于多晶体中小晶粒的混乱排列，总会有若干小晶粒中的某些晶面族恰好能使掠射角θ满足布拉格方程，不同的晶面族要求不同的入射角，因而不同晶面族的衍射线就和原射线形成不同的夹角而射出。用这些方向不同的衍射线就可研究晶体的内部结构，把这些衍射线用拍摄的方法记录下来，然后对底片进行处理计算得到该晶体的点阵常数。这种方法就称为“德拜相法”。
同时，X射线衍射分析的理论还涉及晶体几何学的相关理论，在本书中不再介绍，感兴趣的读者请翻阅相关书籍［16］ 。
有关纳米材料与结构测试方法的文章
研究了采用掠入射Seeman-Bohlin衍射仪、利用X射线衍射图谱导致的双层膜结构变化与退火的关系[3]。从中可观察到Cu5 Sn5和Cu3 Sn的衍射峰均存在，表明了这两种金属间化合物在该退火过程中形成。图3.2和图3.2所示分别为室温下保存1年和在100℃下退火60 h的两个样品的4θ在40°~190°范围内的Seeman-Bohlin X射线衍射图谱。表3.2所示为图3.2中所标记的Cu3 Sn的各个衍射峰。表3.2100℃下退火的双层Cu-Sn薄膜试样得到的Cu3 Sn相各衍射峰的数据续表*和代表长周期超晶格线。......
2023-06-20
图4.11是不同龄期水泥水化物XRD物相分析结果。其中2θ值为18°，d值为4.905处的CH衍射峰强度随龄期变化尤其明显，有研究人员以此峰研究表征水泥水化程度或者水化速率。图4.11图4.11不同龄期水化水泥XRD分析图A—Alite B—Belite CH—Ca2G—AFt C—CaCO3a,b，c和d分别代表龄期为5h、1d、3d和28d......
2023-11-03
经过多次失败，终于得到了第一张X射线衍射图，初步证实了劳厄的预见，于1912年5月4日宣布他们实验成功。几十年中，在X射线光谱学和X射线晶体结构分析两方面做出卓越贡献，从而获得诺贝尔物理化学奖或生理医学奖的学者，竟超过10人！应用X射线晶体结构分析方法于化学物质的结构研究，使现代结晶化学迅速兴起。几何晶体学、X射线晶体学和结晶化学的发展又一次生动地证明了这一点。......
2023-11-24
X射线衍射仪必须要有合适的X射线源，不同的样品对X射线源有不同的要求。X射线光源可分为普通X射线源和同步X射线源。目前世界上的第三代光源共有14台，包括位于上海浦东的同步辐射光源。图4-6上海光源结构平面示意图与一般X射线源相比较，同步辐射光源有如下特征：高强度（高亮度）：图4-7为各种不同类型的X射线的亮度比较。图4-7同步辐射光源光子亮度的进展和比较......
2023-06-20
图4-1X射线管发出的X射线谱普通X射线管产生的X射线具有不同的波长，其X射线谱由连续X射线谱和特征X射线谱组成，具体如图4-1所示。这些射线谱位于特定的波长处，而且波长范围很窄、强度极高，这些线状的射线谱称为特征X射线谱。多余的能量作为X射线的形式发射出来。整个K系X射线波长最短。结构分析时所采用的就是K系X射线。......
2023-06-20
X射线与物质相互作用时，会产生各种不同的、复杂的过程，如图4-2所示。图4-2X射线与物质的相互作用1.X射线的吸收与电子束相同，当X射线遇到任何物质时，都会有一部分的X射线与物质中的原子产生相互作用，能量被吸收，这称为吸收现象，即第一类效应。在本书第3章提及的电子束与样品相互作用后也会产生特征X射线和俄歇电子，同样也可进行样品的元素分析。此时各散射射线之间将相互发生干涉，故称为相干散射。......
2023-06-20
只有了解像衬度的形成机理，才能对各种具体的图像给予正确解释，这是进行材料电子显微分析的前提。总的来说，透射电镜的像衬度来源于样品对入射电子束的散射。对于晶体样品，电子将发生相干散射即衍射。图3-23不同种类样品的衍射花样图3-24包含高阶衍射信息的会聚束电子衍射花样［22］会聚束衍射。普通选区电子衍射适用样品的最小尺寸为0.5μm，现代电镜甚至可对0.1～0.5μm大小的位置作电子衍射。......
2023-06-20
伦琴X射线又称伦琴射线，是1895年由德国物理学家伦琴发现的，波长介于紫外线和γ射线间的电磁辐射。1901年，由于发现X射线而对人类作出贡献，伦琴获得了当年的诺贝尔物理学奖。不过，人类关于X射线的研究并没有停止。在伦琴发现X射线后仅仅几个月时间内，这条发现就被应用于医学影像。而且X射线还是诱发癌症和冠心病的主要原因，因此应该更加防范和注意。......
2024-06-12
相关推荐