从自身参数可以看出，激光跟踪仪的测距精度远高于测角精度，而且随着测量距离的增大，测角误差增大更为明显，符合表1中的观测结果。如图2所示，在Matlab中利用激光跟踪仪自身参数把随机误差注入到观测值中，以模拟点云的形式得到三维坐标的点云分布图。查定额《配合比参考表》,砾石GD40中砂425水泥C15商品混凝土参考价为135.66元/m3,则:图2 激光跟踪仪测量点云分布图......
2023-06-23
椭圆偏振仪的测量分析步骤
【摘要】：也就是说椭偏分析强烈地依赖于拟合模型的选取。Ψmod、Δmod和Ψexp、Δexp分别是椭偏参数的拟合值和实测值。对薄膜的椭偏光谱进行拟合时，需要根据不同的材料特性，赋予每层薄膜合适的色散关系。建立合适的结构模型和色散关系对于光学常数的准确测量十分关键。
1.基本操作和数据处理
典型的椭圆偏振仪的操作和数据处理过程包括：开启→检测→整理→校正→获取数据→分析（Model→Fit→Result）。
2.模型选择和参数拟合
椭偏仪直接测量得到的是不同波长的椭偏参数Ψ和Δ，它们是薄膜的厚度、折射率n（λ）、消光系数k（λ）的函数，并与其有着确定的对应关系，因此是一个数值拟合与反演的问题。于是，要获得所需要的薄膜参数值，关键在于模型的建立。也就是说椭偏分析强烈地依赖于拟合模型的选取。拟合结果的好坏，通常以均方差函数（MSE）来评价
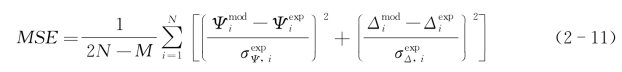
式中：N是角度（Ψ，Δ）对的数目，M是模型中变量的数目，σ是测量数据的标准方差。Ψmod、Δmod和Ψexp、Δexp分别是椭偏参数的拟合值和实测值。
建立光学薄膜系统的模型包括两个方面，一是建立尽量符合实际薄膜样品的物理结构模型，二是要选择能描述该薄膜特性的色散关系。
（1）物理模型的建立。建立的结构模型与实际越接近，计算得到的椭偏参数与测量值就越接近。因此，建立合理的模型特别重要。
对于层数及材料未知的光学薄膜，通常从单层膜的分析开始，首先采用基底＋色散层的基本模型。根据这个模型，可以反演计算出薄膜的光学常数和厚度，如果椭偏参数的拟合结果与实测相差比较大，就需要对上面建立的结构模型进行修正。故此时必须首先考虑薄膜材料的非均质问题，并加以适当修正，否则会严重影响求解结果的精度。对于上面的薄膜，如考虑样品表面可能不是理想的平面，可以在环境和薄膜之间引入一个虚拟的膜层——表面粗糙度层（Srough）来进行拟合。还可以调整薄膜厚度重新给定初值，如果始终得不到理想的结果，说明薄膜很可能不是单层膜。有必要尝试双层薄膜结构，而这时两层薄膜之间可能存在一定厚度的混合层（EMA）。这时薄膜系统可用图2-10所示的多层结构模型来表示。通过再次拟合，仍然得不到理想的拟合效果，可以考虑三层、四层结构，赋予合适的初值及适当的色散关系，直到得到理想的拟合效果。有时薄膜样品的结构模型可能很复杂，但也不是建立的模型越复杂越好，要根据实际情况以最简单且达到最小MSE为原则来确定。
图2-10 多层膜物理结构模型
（2）色散模型的建立。从现象上来看，介质的色散表现为对不同频率的入射光具有不同的传播速度，因而具有不同的折射率。由麦克斯韦电磁场理论可知，介质的折射率及光波在介质中的速度均取决于介电常数。按照洛伦兹的色散理论，色散现象可以解释为介质中带电粒子在光波电场作用下做受迫振动时产生的一种效应，亦即色散现象的实质是光波电磁场与介质分子作用的结果。对薄膜的椭偏光谱进行拟合时，需要根据不同的材料特性，赋予每层薄膜合适的色散关系。实验结果表明，对于大多数透明或弱吸收薄膜，采用Cauchy模型，可以较好地反映薄膜的色散关系，这一关系表示为
式中：A、B、C为拟合系数。如果这一关系不能得到很好的拟合效果，常用的还有Lorentz振子模型、Forouhi-Bloomer模型、Sellmeier模型等。对于某些复杂的结构模型，以上的色散模型可能不适用，这时就应考虑用等效介质（effective medium approximation）来描述等效层。建立合适的结构模型和色散关系对于光学常数的准确测量十分关键。
有关纳米材料与结构测试方法的文章
- 详细阅读
- 详细阅读
-
椭圆偏振仪的应用技术详细阅读
利用椭偏技术可以获得使偏振态发生改变的材料的相关信息。最终拟合得到两层薄膜的折射率及厚度分别为：n1=1.942 1，d1=88.915；n2=2.299 3，d2=108.02，其中接近基底的为第一层。......
2023-06-20
-
椭圆偏振仪基本原理解析详细阅读
下面以单层膜为例，描述椭偏仪的基本原理。椭偏仪的发展过程经历了消光法和光度法，两者的原理略有不同。根据这一原理检测反射线偏振光的方位，根据检偏器的方位得到值。图2-8消光法椭偏仪测试系统基本光路原理图图2-9光度式椭偏法测试装置光谱式椭偏法又称为椭圆偏振光谱法，使用有反射式补偿器或适当的膜层系统补偿器，也可以通过连续改变波长的方法来实现。......
2023-06-20
-
使用钳形接地电阻测试仪测量接地电阻的方法及步详细阅读
钳形接地电阻测试仪是传统接地电阻测量技术的重大突破，在测量有回路的接地系统时，不需断开接地引下线，不需辅助电极，安全快速、使用简便。下面以ETCR2000型钳形接地电阻测试仪为例介绍接地电阻的测量方法。如果钳形表的测量值RT小于接地电阻的允许值，那么这两个接地体的接地电阻都是合格的。3）用钳形表测量接地电阻时，不用打开接地极与引线之间连板，测量的结果包含接地引线电阻，与实际接地电阻接近。......
2023-06-27
-
纳米压痕仪的结构分析详细阅读
图6-19为一个商品化的纳米压痕仪及其工作原理。目前，各种商业应用的纳米压痕仪原理基本相同，它们的差别主要表现在力的加载方式和位移的测量方式上。图6-19压痕仪的结构及内部结构根据前面的介绍，目前的纳米压痕仪的工作模式有两种：普通模式和连续刚性测量模式。压头在纳米压痕仪中是一个重要的部件，测试时需要选择合适的压头。是纳米压痕试验另一个常用的压头。球形压头的初始接触应力小，仅产生弹性变形。......
2023-06-20
-
纳米尺度薄膜厚度测量的常用仪器——台阶仪详细阅读
在上述薄膜厚度的测量方法中，用于纳米尺度薄膜厚度测量的主要有表面台阶仪法和椭圆偏振法。图2-2Nanosurf型台阶仪的实物图台阶仪又称接触式表面轮廓仪，是一种最常见的薄膜厚度和表面粗糙度的测量仪器。1936年，美国的E.J.Abbott成功研制了第一台车间用的测量材料表面台阶高度和表面粗糙度的轮廓仪。1940年，英国的Taylor Hobson公司研制成功了表面台阶测量仪Talysurf。到目前为止，轮廓仪仍是最常用、最可靠的表面台阶高度和表面粗糙度的测量仪器。......
2023-06-20
-
测量员必备技能：水准仪的使用详细阅读
从仪器箱中取出水准仪，用中心旋钮将其与三脚架连接牢固，安置时尽量让圆水准气泡居中。图8-11 概略整平仪器图8-12 瞄准水准尺5）让眼睛在目镜端上、下微动，若看到十字丝与目标的影像有相对移动时，这种现象称为视差。如图8-13b的读数应为1.334m。......
2023-08-20
相关推荐