电磁场中有电路和磁路的概念，热场中也有热路的概念。从这点上讲，把热场简化为热路，其精度比电磁场简化电路和磁路的要低，但通过适当处理也可满足工程计算要求。图5-2 电路与类比的热路a）电路 b）热路表5-1 热路参数与电路参数的类比利用以上热路和电路相似原理可对一具体开关电器建立其热路网络模型，求解热网络问题可采用电网络方法求解，例如用电网络的软件PSpice来计算。另一种求解热网络方法是热网络有限差分法。......
2025-09-29
热迁移驱动力的作用及调控方法
【摘要】：当原子的跃迁距离为3×10-10 m时，驱动力所做的功为Δw＝4.8×10-27 N·m＝4.8×10-27 J，这个结果与我们理论计算出的热迁移时的热能改变量非常接近。因此如果电流密度104 A/cm2可在焊料接头中引起电迁移现象，那么在1 000℃/cm温度梯度下，焊料接头中也能发生热迁移。为了测出Q*，当知道原子通量时，可使用原子通量方程式，并在扩散系数、温度梯度和平均温度已知的情况下计算出Q*。在12.2.4节中，铅原子在热迁移中的转移热已通过使用式被估测出来了。
在热电效应中，温度梯度可驱动电子移动，与此类似的是它也能驱动原子运动。从本质上来说，高温区的电子在扫描和与扩散原子的相互作用中能量更高，因此原子可沿着温度梯度从高到低迁移。关于原子扩散的驱动力，由化学势梯度引起的原子通量可表示为
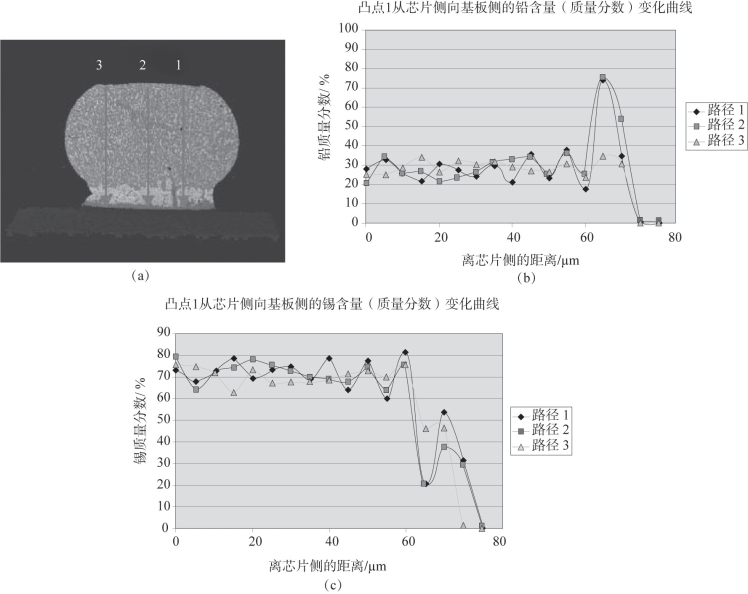
图12.8 凸点照片及铅锡含量分布图
（a）第11个凸点在扫描电镜下的高倍照片；（b）利用电子探针沿图12.8（a）中的1、2、3路径扫描得到的铅含量分布图；（c）利用电子探针沿图12.8（a）中1、2、3路径得到的锡含量分布图
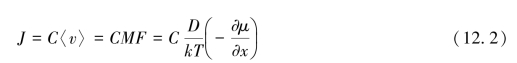
式中，<v>是漂移速度；M＝D/kT是迁移率；μ是化学势。如果将温度梯度视为驱动力，则有
式中，Q表示转移的热。对比式（12.2）与式（12.3），可看出Q与μ有相同的量纲，所以Q表示单位原子的热能。换句话说，如果定义熵S＝Q/T，那么S dT就能表示其热能。
我们将Q定义为运动原子携带的热量和初态时原子的热量差[式（12.1）]。对于从热端迁移到冷端的元素，其由于损失了热量，所以Q为负值；而对于从冷端迁移到热端的元素，Q则为正值。
热迁移的驱动力如下所示：
(https://www.chuimin.cn)
为做简单估算，我们取ΔT/Δx＝1 000 K/cm，考虑到原子跃迁过程中的温度差，取跃迁距离为a＝3×10-8 cm，跃迁前后温差为3×10-5 K，因此热能的改变是
我们可将该数值与电流密度为1×104 A/cm2或者1×108 A/m2的电迁移过程中原子扩散驱动力F进行比较，可得出在焊料合金中诱导电迁移的力F：
取ρ＝10×10-8Ω·m，Z约为10，e＝1.602×10-19 C，故可得F＝10×1.602×10-19×10×10-8×108 A/m2≈1.6×10-17 C·V/m＝1.6×10-17N。
当原子的跃迁距离为3×10-10 m时，驱动力所做的功为Δw＝4.8×10-27 N·m＝4.8×10-27 J，这个结果与我们理论计算出的热迁移时的热能改变量非常接近。因此如果电流密度104 A/cm2可在焊料接头中引起电迁移现象，那么在1 000℃/cm温度梯度下，焊料接头中也能发生热迁移。
至于转移热，我们说过Q可为正值，也可为负值。在Fe-C体系中，我们发现碳以间隙扩散机制迁移到热端，此时转移热为正值。在SnPb合金中，热迁移可使铅从热端迁移到冷端，即沿着温度梯度向低温区域移动，而锡则沿相反的方向迁移，即逆着温度梯度向高温区移动。对于铅，Q是负值，或者说热量下降；而对于Sn，Q是正值，即热量增加。造成这个结果的原因是这两种物质都有一个温度梯度，不像在扩散偶联中，两种相互扩散物质的浓度梯度是在相反的方向，所以化学势的变化可以是正的。
为了测出Q，当知道原子通量时，可使用原子通量方程式（12.3），并在扩散系数、温度梯度和平均温度已知的情况下计算出Q。在12.2.4节中，铅原子在热迁移中的转移热已通过使用式（12.3）被估测出来了。
从图12.8（a）中可测出在基板末端铅的积累宽度（12.5μm），然后通过焊料接头横截面宽度和面积的乘积得到总原子迁移量。取27Sn73Pb密度为10.25 g/cm3，取其分子量为183.3 g/mol，于是可得到通量JTM＝4.26×1014原子/cm2。假定温度梯度为1 000 K/cm，温度为180℃（接近SnPb共晶点），扩散系数DPb＝4.41×10-13 cm2/s，故单位摩尔的转移热QPb为-25 kJ/mol。
如果铅的浓度分布不均匀，那么Q的计算精确度将会受到影响。假定的温度梯度也可能不正确。但是在这里最重要的假设是铅和锡均在温度梯度作用下发生迁移。如果铅是主要扩散元素，且通过扩散从热端运动到冷端，那么在等容扩散过程中锡会沿反方向移动。两相微观结构中锡的反向通量对迁移热计算的影响也应当被考虑在内。
相关文章
- 详细阅读
-
不通电的复合焊点热迁移问题详细阅读
图12.1倒装芯片焊料接头及焊料接头横截面基板上倒装芯片的示意；倒装芯片复合焊料接头的横截面；焊料接头横截面SEM照片为了利用电阻加热引起的温度梯度来研究热迁移，我们制备了两组倒装芯片试样。为了研究热迁移，我们也检测了附近没有通电的凸点。在整行没有通电的焊料接头中热迁移的影响是显而易见的，如图12.2所示，因为在这些凸点中，锡向硅侧迁移，铅向基板侧迁移。......
2025-09-29
-
热迁移现象的原位观察技术详细阅读
据观察，在150℃条件下的电迁移试验中，铅是主要的扩散元素。回流结束后，高铅焊料内会产生Cu3 Sn，但随着锡向热端扩散，Cu3 Sn转变为Cu6 Sn5。在硅侧的整个接触区域内，孔洞和Cu6 Sn5的分布是均匀的。......
2025-09-29
-
限速器的作用及调节方法详细阅读
随着轿厢继续下行，限速器轮槽与限速绳索之间产生摩擦力使限速绳被轧住，带动安全钳联动系统，将安全钳拉杆提起，安全钳楔块动作，轿厢被制动在导轨上。限速拉簧调节螺栓的拉力，可调节限速器的动作速度。当限速器动作后需要复位时，可以将轿厢慢速上行，限速轮反向旋转，棘爪与棘轮脱开，安全钳即可复位。......
2025-09-29
-
熔断器的作用及使用方法详细阅读
熔断器是一种简单而有效的一次性保护电器。螺旋式熔断器螺旋式熔断器是机床上使用较多的熔断器，在它的熔体上端带有熔断指示器，当熔体熔断时指示器自动脱落，可透过瓷帽上的玻璃孔观察到。5）熔断器的额定分断能力必须大于电路中可能出现的最大故障电流。6）若使用新型熔断器时，应参照其有关说明书进行选择。图1-37 熔断器的图形和文字符号......
2025-09-29
-
热振试验方法及设备介绍详细阅读
热振试验也称为热冲击试验，用以检验热障涂层耐急冷急热的能力。设置不同的温度、保温时间和冷却速度，可进行不同的热振试验。这里主要介绍电炉加热水冷却的热振试验方法。采用电阻丝加热的马弗炉作为加热炉，加热温度控制在试验设置温度±5℃的范围，对于Al2O3涂层试验温度设定为800℃，对于ZrO2涂层试验设定温度为900℃，也可根据协商另定试验温度。......
2025-09-29
-
引纬的作用及方式详解详细阅读
(一)引纬的作用引纬是以引纬器或高速射流将纬纱引入梭口，与经纱形成交织。(二)引纬的方式1.有梭引纬 梭子内装有携带一定数量纬纱的纡子，在左右投梭棒的交替打击下在梭口内循环往复运动，带引纬纱穿越梭口、绕( 折) 返布边，即为梭子引纬。我国目前仍有一定数量织机在使用这种引纬方式。采用无梭引纬方式的织机被称为无梭织机，其按引纬方式不同可划分为喷气织机、喷水织机、剑杆织机和片梭织机。......
2025-09-29
-
液压系统卸荷回路：作用及实现方法详细阅读
1）卸荷回路的作用是：液压泵的卸荷就是让液压泵以很小的输出功率运转，或以很低的压力运转，或让液压泵输出很小流量的液压油。使用电磁溢流阀也可以形成相同工作原理的卸荷回路。图6-10所示为使用限压式变量泵实现零流量卸荷的回路。图6-9 外控式顺序阀卸荷回路1—低压大流量泵 2—高压小流量泵 3—溢流阀 4—卸荷阀图6-10 限压式变量泵实现零流量卸荷回路1—泵 2—换向阀 3—液压缸 4—溢流阀......
2025-09-29
相关推荐