在锅炉、化工、电力及核电等领域的管线以及换热器的生产和安装中，存在大量的管-管和管-管板的焊接，通常都采用TIG焊方法。为了保证一定的余高，焊前将管端适当扩口或者添加填充焊丝，也可以用TIG焊打底后再用焊条电弧焊盖面。......
2023-06-26
封装板的竖直跌落和焊球上的扭矩优化技巧
【摘要】：图11.13所示为连接到基板上的焊球及其基板的自由下落示意。若假设板垂直下降，其边缘处以速度v撞击地面，在撞击地面时，板和焊球的速度都将从v变为零，然后变为-v。短时间将产生大的剪切力和扭矩。因此在设计跌落测试时，Δt的定义与测量是最关键的环节。应力分布产生的总力矩应等于扭矩。如上所述，σmax取决于扭矩，而扭矩取决于力，力取决于Δt。我们可根据σmax的大小确定跌落能否导致裂纹在界面处形成。
图11.13所示为连接到基板上的焊球及其基板的自由下落示意。若假设板垂直下降，其边缘处以速度v撞击地面，在撞击地面时，板和焊球的速度都将从v变为零，然后变为-v。焊球的动量变化将为Δ（mv），其中m是焊球质量。该变化将导致剪切力F和扭矩Q作用在球上，且它们趋于破坏焊球和板之间的界面。力可根据下述关系式进行计算：
式中，Δt是速度从v到零再到-v的变化时间或动量变化的过渡时间。短时间将产生大的剪切力和扭矩。由于我们可以很容易得到（或测量）自由下落速度v和质量m，而过渡时间和减速度会直接影响力和扭矩的大小，因此如何精确测量过渡时间Δt或减速度-a非常关键。因此在设计跌落测试时，Δt的定义与测量是最关键的环节。
当力确定时，我们可获得扭矩Q＝F×r，其中，r是焊球重心到界面的最短距离。力F倾向于剪切球和板之间的界面，而扭矩Q将在界面上施加法向力。但是由扭矩引起的法向力分布为上端受拉、底端受压，其应力分布如图11.14所示。
图11.13 焊球及其基板的自由下落示意
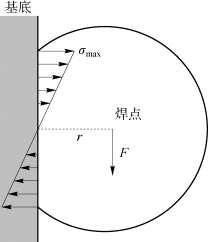
图11.14 应力分布
为了分析应力分布，我们在图11.14中考虑连接到垂直板上的焊球的横截面示意。我们假设焊球和基板之间的接触面积是矩形的，宽度为w，长度为2R。假设从上半部中的张力到下半部中的压应力的分布呈线性变化。如果两端的最大应力取±σmax，则从几何关系可得下述关系：
式中，σ是距离中间原点的距离为z位置处的法向应力，其中原点处法向应力为零。应力分布产生的总力矩应等于扭矩。通过一个非常简单的分析可以计算出扭矩，其为
在最后一个方程中，σ（w d z）是在距离原点z处作用于（w d z）的细条带上的力，因此zσ（w d z）是力矩。总力矩应等于扭矩，即F×r，所以可得
当测量出冲击所造成的扭矩时，通过式（11.8），我们能计算得到σmax。如上所述，σmax取决于扭矩，而扭矩取决于力，力取决于Δt。我们可根据σmax的大小确定跌落能否导致裂纹在界面处形成。除由于扭矩产生的法向力外，界面还经受剪切力。因此在讨论裂纹产生和传播时，在焊料接头的上角和下角处必须同时考虑法向力和剪切力。
有关电子软钎焊连接技术 材料、性能及可靠性的文章
- 详细阅读
-
绘制前后肋板的步骤和技巧详细阅读
1）按照2.8.2节中的方法把图2.8-11中后肋板的轴面投影图导入到UG中。3）绘制前肋板横截面，以正导叶前面为草图平面进行绘制，外圆直径是460mm，内圆直径是335mm，如图2.8-14所示。图2.8-13 后肋板回转图2.8-14 前肋板横截面图图2.8-15 前肋板横截面拉伸5）最后进行“求和”，对所有部件进行求和，完成径向导叶绘制。......
2023-06-26
-
TIG焊操作技巧：手工和自动焊的不同方式详细阅读
TIG焊可分为手工TIG焊和自动TIG焊两种，其操作技术的正确与熟练程度是保证焊接质量的重要前提。由于焊件厚度、施焊姿势、接头形式等条件不同，操作技术也不尽相同。完成这一动作后，将电弧立即恢复原位继续焊接。采用“热接头”法，既能保证质量，又可提高工效，但要求操作技术熟练，动作快而准。施焊过程中断或更换焊丝或与定位焊焊缝接头操作见第十章第二节。......
2023-06-23
-
铜及铜合金的焊前预备和焊后处理技巧详细阅读
铜及铜合金焊丝及焊件的焊前化学清理见表5-5。为了防止预热热量的散失，预热时，铜及铜合金焊件应采取隔热措施。对于要求较高的铜合金焊接接头，在焊后采用高温热处理，消除焊接应力和改善焊后接头韧性。例如，锡青铜焊后加热至500℃，然后快速冷却，可以获得最大的韧性；对于铝的质量分数为7%的铝青铜厚板的焊接，焊后要经过600℃退火处理，并且用风冷消除焊接内应力。......
2023-06-15
-
MAG焊熔透控制优化技巧详细阅读
通过对MAG焊过程进行工艺试验，来寻找其焊接参数和熔池形状之间的关系，为MAG焊过程的熔透控制奠定良好的基础。MAG焊过程中典型熔池形状变化周期见表5-3-4。如果在MAG焊熔透控制中仍然采用和TIG熔透控制一样的方法：仅仅从熔池正面采集图像，控制焊接电流，这是比较困难的。对于熔化极气体保护焊的熔透控制，用区分不同工艺采取相应的控制策略。总之，对于熔化极焊接的熔透控制尚需进行很多探索性的研究。......
2023-06-26
-
如何打保龄球-起源、规则和技巧详细阅读
保龄球又叫地滚球，起源于德国，是一种在木板球道上用球滚击木瓶的室内体育运动。保龄球具有娱乐性、趣味性、抗争性和技巧性，给人以身体和意志的锻炼。保龄球的重量基本上从6磅到16磅，11个级。为使保龄球有一个平稳的加速度，投球前必须进行助跑。......
2023-08-11
-
埋弧焊的坡口清理和引弧准备技巧详细阅读
④清理坡口及其两侧20mm范围内的铁锈、油污、氧化物等,使其露出金属光泽。引弧板及引出板尺寸:100mm×100mm×12mm。3)准备引弧将焊接小车拉到引弧板处,调整小车行走方向开关位置,并锁紧小车行走离合器;再按下焊丝“向上”或“向下”的方向按钮,使焊丝端部与引弧板可靠接触;最后将焊剂漏斗门打开,使焊剂覆盖焊丝头。同时,随时根据情况作出调整。......
2023-06-27
-
如何优化MEMS器件的封装工艺？详细阅读
特殊的封装环境某些MEMS器件的工作环境是气体、液体或透光的环境，MEMS封装必须构成稳定的环境，并能使气体、液体稳定流动，使光纤输入低损耗。低应力在MEMS器件中，具有微米／纳米级尺寸的部件精度要求高，但结构脆弱易断裂，因此封装所产生的应力应尽可能小。近年来，随着科学技术的发展，在MEMS封装中已广泛采用喷印工艺［23]，这种工艺无需掩膜，经济有效，不涉及湿法工艺。......
2023-06-15
相关推荐