我们称这一现象为热迁移或电迁移诱发的“相分离的共晶效应”,而关于热迁移的内容将会在本书第12章进行论述。这两种合金以图4.5中150℃等温线上的A、B两点表示。因此,若焊料中热迁移或电迁移导致了分离,仅意味着体积分数梯度的改变,而非化学势梯度的改变。因此,相比于PbIn等单相合金中,组分的改变可导致浓度梯度的改变从而产生阻碍相分离的作用力,共晶SnPb等两相混合物的相分离非常明显。......
2023-06-20
根据共晶相图,共晶合金在共晶温度以下的微观结构中包含两个主要相。通常,两个相形成层片状微观组织结构。由于这两个相之间相互处于平衡稳态,因此它们之间没有化学势差,并可能两个相受外因诱导而再分布后,也没有任何反向作用去阻挡该变化。例如,除了两相层片间界面总面积最小化原则外,在层片状组织中每个相并没有明确的厚度。因此,在极端情况下的外部作用力的驱动下,两相可能可以被完全分离成两部分,其中一相在一边,而另一相在另一边。的确,这种极端情况已经被Brandenburg和Yeh所证明真实存在于150℃下的共晶锡铅焊点所发生的电迁移现象中。图4.6(a)和图4.6(b)所示为在发生电迁移前后SEM下的共晶锡铅焊点。在电迁移后,我们看到两相几乎完全分离。同时,在如9.5节中所讨论的复合材料焊点的电迁移,电迁移诱导锡与铅元素的再分布,分别偏析到阴极处和阳极处。在本节,我们介绍在电迁移驱动下,共晶两相混合物的相分离的动力学分析。
在共晶两相混合物中,由于两相彼此在平衡态下共存,在恒定温度下的浓度的变化并不意味着化学势的变化。混合物发生偏析意味着两相体积分数的变化,换句话说,它会导致产生一个体积分数(Volume Fraction)梯度,而不是一个化学势梯度,所以我们不会有根据菲克第一定律所主导的扩散通量。体积分数梯度不是原子扩散的驱动力,体积分数的再分布不会因其上坡扩散而在化学力的作用下被抵消。因此,共晶两相混合物里的偏析现象是非常显著的。该现象独特的地方在于由于缺少反作用力,偏析的物质浓度并不能通过扩散过程而变得平滑。在扩散方程中,浓度随时间的变化速率dC/dt,等于浓度的空间坐标的二阶导数d2C/dx2,乘以扩散率。因此,随着时间的推移二阶导数使物质浓度变化趋于稳定。如果没有它,而且因为我们没有菲克第一定律来描述扩散通量,则物质的扩散过程趋于随机化。我们将在下面内容阐述该现象发生在共晶混合物的电迁移中。在该过程中我们不能使浓度平滑变化,而是会发现其呈随机状态或随机相分布在两相结构中。
在本章9.5节中,我们曾讨论在复合材料焊点的电迁移中,当铅原子被驱至阳极时,锡则会反向扩散到达阴极。而正是反向扩散至阴极的锡导致了最终的失效。因为我们本期望锡原子也会在电迁移的驱动下从阴极移动至阳极,所以说这种逆向扩散过程是很令人感到困惑的。在下面内容中,我们将在假定恒定体积的限制条件下,分析两相结构中物质迁移扩散通量的动力学过程。而这种恒定体积限制条件会最终导致上述逆向扩散过程。
在一个共晶系统的两相结构中,合金成分并不受共晶点的限制。在共晶温度下,它是一个两相混合物,并可以拥有两个主要相中所包含的任何物质成分。在下面的分析过程中,主要假设如下:①在临界区域内,样品的体积和形状守恒(体积通量均衡),意味着没有孔洞或小丘的形成。有两种方式均衡体积通量,分别是通过背应力和柯肯达尔晶格转变。②扩散通量中不包含如菲克第一定律中的浓度梯度项,而是利用漂移速度来描述扩散通量的,即用迁移率与驱动力的乘积来表示。我们将会分析浓度梯度的轮廓线的稳定性问题,并且阐述在电迁移的作用下共晶结构中浓度梯度的轮廓线将会展现随机性的趋势。
考虑一个几乎为纯组元的两相混合的情况,所以之后的分析过程中的数字1和2既代表相也代表物质种类。因为我们将分析过程限制在临界区域内,所以样品形状保持不变,且在样品中的所有区域都有恒定体积的限制条件。这意味着在实验室的参考系下,两类物质的体积通量总和应当处处为零:
![]()
式中,J1,J2为单位面积上的原子通量;Ω1,Ω2为原子体积。为了方便起见,我们引入参数p1,p2作为两相在局部区域的体积分数:
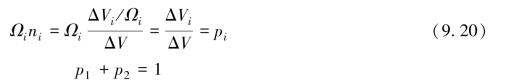
式中,ni为物质种类1或2在单位体积上原子个数。在粗化的空间尺度下,单位体积ΔV至少包括几个晶粒。
各组元的电迁移扩散通量可以通过标准表达式写为
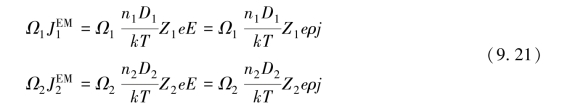
这里我们再次注意,式(9.19)中有恒定体积的约束条件意味着这些通量表达式应当包含额外的对流扩散项。为了满足式(9.19)恒定体积的约束条件,我们假设有两种可选的方法——背应力和晶格转变,或者是这两种方法的组合。
有关电子软钎焊连接技术 材料、性能及可靠性的文章

我们称这一现象为热迁移或电迁移诱发的“相分离的共晶效应”,而关于热迁移的内容将会在本书第12章进行论述。这两种合金以图4.5中150℃等温线上的A、B两点表示。因此,若焊料中热迁移或电迁移导致了分离,仅意味着体积分数梯度的改变,而非化学势梯度的改变。因此,相比于PbIn等单相合金中,组分的改变可导致浓度梯度的改变从而产生阻碍相分离的作用力,共晶SnPb等两相混合物的相分离非常明显。......
2023-06-20

用于热迁移测试的共晶37Pb63Sn倒装芯片焊料接头的测试结构与图12.2很相似,其有11个凸点。而通电凸点附近的未通电的凸点将用来研究热迁移。图12.7所示为四个未通电的凸点在电迁移测试后的横截面SEM照片。图12.7四个未通电的凸点在电迁移测试后的横截面SEM照片图12.8所示为未通电凸点的横截面高倍照片,图中Sn和Pb的重新分配表现在:铅大量积累在了冷端(基板端),热端处(芯片端)没有锡积累。......
2023-06-20

在另一种情况下,完全没有背应力,这意味着可能产生的应力将全部通过晶格转变被立即释放掉。柯肯达尔晶格转变隐含的假设是,空位浓度在扩散区域处处处于平衡状态,所以在阴极不会有孔洞形成,而在阳极也不会有小丘形成。在这里我们将背应力与柯肯达尔转变的物理模型进行比较。在室温下,焊料的扩散依然相当快,而此时很有可能的是,柯肯达尔转变和背应力机制将共同产生作用,锡被推至阳极处。......
2023-06-20

我们将在铝互连的电迁移中所讨论的背应力原理应用在两相共存的混合物的电迁移中。在低于或高于临界应力时,扩散通量则不再相等且逆转反向。式描述了在背应力下电迁移所驱动的偏析现象。我们能够看到,在背应力作用所致通量均衡的情况下,偏析速率由扩散较慢的物质所决定。......
2023-06-20

目前,几乎所有的共晶无铅焊料都是锡基的。表格1.1对比了二元共晶无铅焊料和锡铅共晶焊料的熔点。表1.1二元共晶无铅焊料和锡铅共晶焊料Zn价格便宜且很容易获得,但是它会迅速形成一层稳定的氧化膜,导致波峰焊过程中出现大量残渣,更糟糕的是,由于这层致密氧化膜的存在,这种焊料的润湿性很差,因此,焊接时需要特殊的气体环境。对于Sn-Cu共晶焊料来说,仅含有质量分数为0.7%的Cu,所以焊料几乎是由纯Sn组成。......
2023-06-20

据观察,在150℃条件下的电迁移试验中,铅是主要的扩散元素。回流结束后,高铅焊料内会产生Cu3 Sn,但随着锡向热端扩散,Cu3 Sn转变为Cu6 Sn5。在硅侧的整个接触区域内,孔洞和Cu6 Sn5的分布是均匀的。......
2023-06-20

直流电迁移中存在着极化效应。然而我们需要考虑的是电迁移过程中热迁移的贡献。当电迁移产生的焦耳热在焊料接头上引起了1 000℃/cm的温度梯度时就会出现热迁移。若假设硅芯片侧的温度较高,热迁移就会驱使主要扩散元素向下运动,其方向与下移电子引起的电迁移相同,因此电迁移和热迁移效应会累加。然而在右侧的凸点中,电迁移会使原子向与热迁移相反的方向运动,即这两种迁移效果互相抵消。......
2023-06-20

实验借助弱活性松香助焊剂,将SnPb共晶合金小球在Cu箔上熔化,从而制备得到SnPb共晶焊料在Cu上润湿的试样。熔融SnPb共晶焊料在Cu上的润湿角稳定在11°。SnPb共晶合金在Cu箔上的一个相当特殊的润湿行为就是围绕着球冠状焊料帽的前沿、在Cu箔表面润湿带或润湿环的形成。图2.6所示为SnPb共晶焊料在Cu箔表面上铺展时润湿环的SEM照片。图2.6SnPb在Cu上铺展时润湿环的SEM照片30 s;1 min;5 min;10 min图2.7200℃下润湿环的生长速率......
2023-06-20
相关推荐