各种纯金属的表面张力的大小，可根据金属原子体积大小及绝对熵这两个因素来判断。对同一种金属及合金而言，影响表面张力的因素有：温度、杂质及合金元素、结晶形状、熔剂。......
2023-06-26
接触界面扁平型孔洞的动力学分析
【摘要】：图9.17所示为扁平型孔洞在接触面上生长的原理示意。由于空位扩散场源所造成的沿界面的横向扩散通量可以写为图9.17扁平型孔洞在接触面上生长的原理示意式中，Dint是界面上的扩散率；b′是电流集聚区域宽度；ΔC为在孔洞顶端或孔洞生长前沿处，空位处于平衡态与高电流密度下的浓度差。假设孔洞的初始宽度是d，Jvoid是孔洞顶端的空位扩散通量。表9.3电迁移中扁平型孔洞生长速率的理论值与试验值之间的对比
图9.17所示为扁平型孔洞在接触面上生长的原理示意。弯曲的实线箭头代表电流集聚效应。垂直的实心箭头代表从焊料凸点的顶部到底部由电流集聚效应所驱动的原子扩散通量。虚线箭头代表从焊点基体移动到界面处的空位的反向扩散通量。如果忽略Cu6 Sn5中空位的通量，焊点中空位的通量可以写为
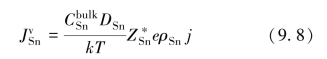
式中，D是扩散率；e是电子的电荷；ρ是电阻率；j是电流密度；Z*是电迁移的有效电荷数。
焊料/金属间化合物的界面为过剩空位提供了扩散通道，使它们能够沿着界面扩散。由于空位扩散场源所造成的沿界面的横向扩散通量可以写为
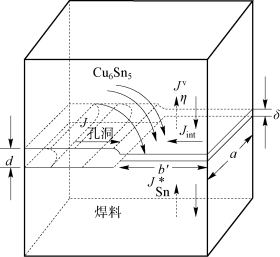
图9.17 扁平型孔洞在接触面上生长的原理示意
式中，Dint是界面上的扩散率；b′是电流集聚区域宽度；ΔC为在孔洞顶端或孔洞生长前沿处，空位处于平衡态与高电流密度下的浓度差。考虑到质量守恒定律，则有
式中，δ是有效宽度界面；a是单位长度。
假设孔洞的初始宽度是d，Jvoid是孔洞顶端的空位扩散通量。我们再次利用通量守恒条件：
将式（9.10）代入式（9.11）中，则供孔洞生长的空位通量可以写为
由Jvoid沿着界面所传输物质的体积为
式中，A＝aδ；ΔV＝adΔl；Ω是原子体积。
将式（9.12）代入式（9.13）中，孔洞的生长速率变成
假设
，我们得到
为了证实孔洞的生长机制，主要的两个参数是电流集聚区的宽度b′和孔洞的宽度d。如图9.17所示，Gibbs-Thomas效应可能对孔洞顶端的形成起到了重要的作用：
式中，γ为单位面积的表面能。
利用线性关系近似，我们得到孔洞的宽度为
由于这个模型是二维的，我们假定孔洞宽度保持不变。另一方面，我们从式（9.9）和式（9.10）可以得到电流集聚区域宽度
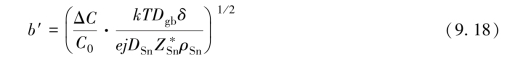
如图9.18所示，二维仿真模型中共晶锡银铜焊点的接触窗口长度取值为224μm，电流集聚区域宽度约为整个长度的15%，因此，电流集聚区域宽度约为33.6μm。根据图9.7，我们测得孔洞的宽度d为2.44μm。电迁移测试温度为146℃，电流密度约为3.67×103 A/cm2，孔洞长度为33μm，孔洞生长的时间是6 h，因此孔洞的生长速率约为5μm/h。在另一种情形下，如9.4.1节中讨论的共晶锡铅焊料凸点，电流密度为2.25×104 A/cm2，测试温度为125℃，接触窗口的长度为140μm，电流集聚区域宽度约为9μm。孔洞在第38 h内形成，焊点在第43 h失效，孔洞的生长速率约为28μm/h。
锡的扩散率DSn＝1.3×10-10 cm2/s，界面的扩散率取值为4.2×10-5 cm2/s。锡的有效电荷数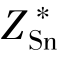
＝17，电阻率ρSn＝13.25μΩ·cm。表面能γ＝1015 eV/cm2，Ω取值为2.0×10-23 cm3。有效界面宽度约为0.5 nm。唯一未知参数是ΔC和C0的比值，为了得到合理的结果，ΔC/C0的取值范围为1%~3%。
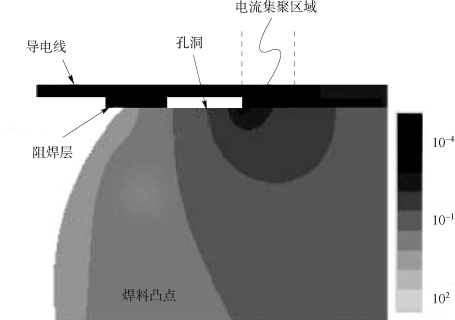
图9.18 扁平型孔洞生长的二维仿真模型
利用这些参数和试验条件数值，可由式（9.18）、式（9.17）和式（9.15）分别算出电流集聚区域长度b′、孔洞宽度d和孔洞的生长速率v的理论值。如表9.3所示，理论值和试验结果比较吻合。
表9.3 电迁移中扁平型孔洞生长速率的理论值与试验值之间的对比
有关电子软钎焊连接技术 材料、性能及可靠性的文章
- 详细阅读
-
孔洞演化特性模拟与分析详细阅读
图2.14应力－应变曲线和缺陷总体积演化关系图图2.15为构件焊接区域两个孔洞型缺陷比较集中的区域中孔洞型缺陷体积随塑性应变增加的变化曲线和相应的应力－应变曲线，以及对应的加载过程中这两个区域中孔洞型缺陷形貌的演化过程示意图。图2.16的扫描观测结果表明，随着焊接区域塑性变形的增加，焊缝区域不......
2023-08-26
-
双列角接触轴承中的载荷分布分析详细阅读
对列角接触轴承可以承受任意方向的载荷，如图2-28所示。表2-13 双列轴承的载荷分布积分JrJa作用于轴承的载荷可有下列三种情况：1）Fa=0。这时轴承上仅有轴向载荷Fa，轴承中只有一列滚动体承受载荷，且此列各滚动体承受相同的载荷。这时轴承中两列承受载荷不同，Ⅰ列较大，Ⅱ列较小。如果Fa大于上述之值，则双列轴承完全像一个单列向心推力轴承那样起作用。......
2023-06-26
-
偏心轴动力学输出特性分析详细阅读
在工作室气体合力的作用下推动转子旋转，从而带动偏心轴旋转对外输出扭矩。从图2.38可以看出，偏心轴轴颈的受力也是周期变化的，这是由于离心惯性力在转速不变的情况下是不变的，偏心轴轴颈的受力变化情况只与气体作用力相关。图2.37偏心轴输出扭矩图2.37偏心轴输出扭矩图2.38偏心轴轴颈受力图图2.38偏心轴轴颈受力图......
2023-06-23
-
P型接触在GaN上的应用挑战及解决方法详细阅读
GaN上的p型接触是一项复杂的挑战。退火可在不同环境下完成，但只有氧环境会形成p型欧姆接触。这些p型接触的退火通常在500～600℃的空气或氧气环境中实现的。所以许多器件包含镍/金p型接触。对于这些材料，问题仍在于良好p型接触的实现。对于先进结构的LED，p型接触掩埋于其中并且也具备光反射器的功能，这时常规的镍/金接触不再适用。......
2023-06-15
-
球队阵型的重要标杆及对手阵型分析详细阅读
球队的阵型是职责分配的重要标杆，大致决定了球员在场上需要承担怎样的责任。在2018 年赛季，笔者有幸拜访了英超的一家俱乐部，并与时任的一线队比赛分析师探讨了赛前准备的话题。在他们的报告里，分析师交给主教练的对手阵型分成四个部分，也就是在不同阶段对手有着四个阵型。......
2023-11-01
-
偏执型人格障碍患者的行为动力学及干预策略详细阅读
偏执型人格障碍患者的行为动力学包括投射和投射性认同的成分。根据DSM-IV-TR，偏执型人格障碍至少会表现出以下几种症状。这些患者的亲属中有较高的精神分裂谱系障碍的发病率，因此，偏执型人格障碍的症状可能是另一种障碍的发病前阶段。偏执型人格障碍患者可能会为他们的独立和客观而引以为傲，他们还可能会认为那些容易表达情感的人脆弱、麻烦。干预策略对于偏执型人格障碍患者，个体治疗是最好的选择。......
2023-12-01
-
角接触轴承载荷分布优化分析详细阅读
角接触球轴承和圆锥滚子轴承可以同时承受径向载荷和轴向载荷，如图2-23所示。但是单个角接触球轴承和圆锥滚子轴承不能单独承受纯径向载荷。图2 - 23 角接触球轴承图2 - 24 角接触轴承内圈载荷分布图此类轴承中的载荷分布与载荷角β有关。轴承中任一滚动体承受的载荷，由滚动体与滚道接触处的变形量来决定。表2-12 单列角接触轴承的载荷分布积分Jr、Ja 单列圆锥滚子轴承32315承受的径向载荷Fr=40kN，轴向载荷Fa=15kN，试计算轴承中最大滚动体载荷Qmax。......
2023-06-26
相关推荐