电流集聚效应与电流密度梯度力的作用

2023-06-20 理论教育版权反馈

【摘要】：电流集聚区的势能梯度为这些缺陷从高电流密度区向低电流密度区移动，提供了其所需的驱动力。因此，孔洞往往形成在低电流密度区域，而不是在高电流密度区域。但这并不符合真实情况，因为孔洞的形成发生在低电流密度区。当电流集聚时，存在一个电流密度梯度，就会存在这样一个驱动力：这个力驱使多余的空位朝垂直于电流的方向扩散。

超大规模集成电路技术中的互连为三维多层结构。当电流转向或汇聚时，例如，在三维结构中当电流从一层互连到另一层时，电流集聚效应发生并且显著作用于电迁移现象。我们设想，如空位和溶质原子等缺陷，很有可能在高电流密度区的势能比低电流密度区的势能要高。电流集聚区的势能梯度为这些缺陷从高电流密度区向低电流密度区移动，提供了其所需的驱动力。因此，孔洞往往形成在低电流密度区域，而不是在高电流密度区域。换句话讲，在三维互连中，缺陷所导致的失效有很大可能发生在低电流密度区域[32-33]。

图8.10（a）所示为著名的Blech短条带电迁移测试结构的截面示意。首先，我们假设电子从左（阴极）向右（阳极）运动。钨基线电阻高于短铝条带，所以电子会绕过钨基线进入铝条带中，因为后者是一个更好的导体。当电流进入铝带的区域时，就会发生电流集聚效应。我们对电流集聚效应进行计算机模拟仿真计算，其结果如图8.10（b）所示。箭头所指左上角及其附近部分为低电流密度区。在图中可以清楚地看出，在发生电流集聚效应的区域，即铝/氮化钛界面左下角处，为高电流密度区[34-36]。

许多SEM照片表明，在电迁移的作用下孔洞的形成发生在条带的阴极区域。如果孔洞形成并生长在高电流密度区，如图8.10（c）所示，那么它将不能扩展到左上角的低电流密度区，由于孔洞实际上为电路开路，这样电流路径会被推回到阳极。为了完全耗尽阴极，孔洞必须扩散到低电流密度区，所以孔洞必须从条带左端的左上角开始形成。

图8.11所示为通过钨垂直连接的两级铝互连结构的截面示意。再次假设电子方向是从左到右，通过钨通道时发生电流集聚效应。我们认为左端钨通道与左上角箭头所指之处及其临近区域是低电流密度区域，也是孔洞首先形成的区域。因为在钨中的原子扩散比在铝中慢得多，钨/铝界面是扩散通量的有源平面（Divergence Plane），更多的铝原子从此界面处离开。孔洞的反向通量将导致孔洞在靠近界面处聚集。但孔洞不会在钨/铝界面右侧，即电流密度最高处形成，它往往形成于左上角或邻近区域。随着孔洞的扩展，当覆盖整个钨通道时，它便导致电路通道断开，最终引起电路系统失效。在微电子工业中，这被称为磨损机制故障。推迟磨损机制故障的一种方法是，在钨通道上方增加一个铝的悬臂梁结构，如图8.11中虚线所示。该悬臂梁结构提供了孔洞生长所需的额外的吞吐体积，所以它可以延长平均失效到达时间。然而，这个解决方案的隐含假设条件为，孔洞将进入低电流密度的悬臂梁所在区域。

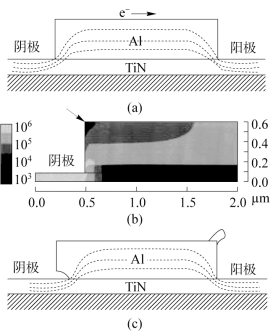
pagenumber_ebook=179,pagenumber_book=165

图8.10　电迁移测试结构图及仿真图

（a）Blech短条带电迁移测试结构的截面示意；（b）电流集聚效应计算机模拟仿真结果云图；（c）孔洞形成并生长的区域

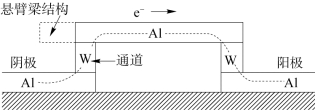
pagenumber_ebook=179,pagenumber_book=165

图8.11　通过钨通道连接的两级铝互连结构的截面示意

通常假定有一个应力梯度驱动孔洞向低电流密度区运动。应力梯度在空位形成之后能建立起来是由于材料拥有自由表面。孔洞形核需要具有过饱和的空位浓度，因此空位必须先扩散到低电流密度区，之后孔洞才能形成。在电子风力的作用下，我们预想空位将会流向高电流密度区，并在那里形成孔洞。但这并不符合真实情况，因为孔洞的形成发生在低电流密度区。

设想有一种驱动力，使空位从高电流密度区向低电流密度区运动，我们在单晶铝条带中进行以下分析，并假设在铝的晶体晶格中，一个空位所具有的比电阻率为ρv。其比电阻率可能取决于电流密度，这是由于焦耳热的产生导致电阻率对温度存在依赖关系。不过，为了简化模型，我们在这里忽略温度的影响，以下的简化分析都认为其只受电流密度影响。因为空位是一种晶格缺陷，我们可以将其比电阻率视为原有晶格原子的电阻率的额外值。在电迁移试验中，当电流密度为je时，空位周围将出现电压降，其大小为jeρv。从能量的角度来看，我们可以认为空位电势高于周围的晶格原子电势，其电势差为jeρv。如果知道空位的电荷，在电流密度为je的情况下，我们就能得到空位所具有的电势能。令空位的电荷是Z**e，其中，Z**是空位的有效电荷数，e是电子元电荷，那么，当电流密度为je时，空位所具有的电势能为Pv＝Z**ejeρv。

如果我们假设在没有任何电流（je＝0）的情况下，热力学平衡态下的晶体具有空位浓度Cv：

式中，晶体的原子浓度为C0；空位的形成能为ΔGf。那么，当电流密度为je时，空位浓度将减少到

在一个均匀的高电流密度下，晶体的平衡空位浓度降低。换句话说，电流不喜欢额外的高电阻值障碍（或缺陷），并且其更愿意消除它们，直到达到平衡态。当电流集聚时，存在一个电流密度梯度，就会存在这样一个驱动力：

这个力驱使多余的空位朝垂直于电流的方向扩散。现在如果我们回到图8.10（a）中，考虑短条带中的电迁移通量，在条带中间部分，电流密度是常数，所以从左指向右的铝原子扩散通量也是常数，进而会有空位通量从右指向左去平衡该原子的扩散作用。靠近表面或基底部分的少量空位会跑到表面或者基底的界面处，但由式（8.31）可知，其浓度保持不变。当空位扩散通量靠近阴极，并进入电流集聚区域时，其中大部分成了过剩空位，并且有一种力开始发挥作用，使它们向低电流密度区移动。因此，空位扩散通量具有垂直于电流方向的分量：

式中，Dv/（kT）与Dv分别是晶体中空位的迁移率和扩散率。由于电迁移效应，空位总是有一个从阳极到阴极的恒定的扩散通量，指向阴极的空位扩散总通量，可以分解为两个扩散通量分量：

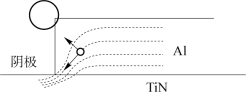
pagenumber_ebook=180,pagenumber_book=166

图8.12　在两种力作用下空位的运动

式中，第一项是由电迁移在电流密度（电子风力）驱动下产生的，第二项是由电流集聚效应在电流密度梯度驱动下产生的。Z*是在铝原子中扩散的有效电荷数，并且E＝jeρ（ρ是铝的电阻率）。在这里，我们假设空位通量的方向与铝相反但其大小等于铝的扩散通量。此外，括号中的是一个矢量求和，第一项的方向是沿着电流方向，第二项的方向垂直于电流方向。换句话说，在电流集聚区中的空位会受到两个力的作用，如图8.12所示。由于电流在电流集聚区域中转向，Jsum的方向会随位置变化。显然，我们需要一个更为细致的模拟仿真，来获得在电流集聚区域中的力的大小和分布。

我们对该梯度力的大小是非常感兴趣的。如果我们在短条带上施加105 A/cm2的电流密度，并且假设通过厚度为1μm的短条带中的电流密度会逐渐降至0，那么其电流密度梯度将高达109 A/cm3。该梯度力与电子风力大小在数量级上相当。在这么大的梯度之下，高阶效应可能存在，但我们暂且忽略这一效应。

倒装芯片焊点中的电流集聚效应及其在电迁移引发的故障中的影响将在9.3节进行介绍。

电流集聚效应与电流密度梯度力的作用

相关推荐