电力系统的短路故障通常称为横向故障，它指的是在网络的节点f处出现了相与相之间或相与零电位点之间不正常接通的情况。发生横向故障时，由故障节点f同零电位节点组成故障端口。造成非全相断线的原因很多，例如某一线路单相接地短路后故障相开关跳闸；导线一相或两相断线；分相检修线路或开关设备以及开关合闸过程中三相触头不同时接通等。图12-18用对称分量法分析非全相运行......
2025-09-29
计算有效电荷数的方法
【摘要】：为了得到扩散原子的散射截面，即<>，我们假设该扩散原子与图8.4所示的临近原子获得了扩散动能ΔHm，该参数独立于温度变量：那么，将式与式作比，则得出的就是散射截面的比值：式表明该比值和温度成反比。例如，在480℃下，对于铝的Z*的测量值和计算值分别为-30和-25.6。图8.5金原子的Z*随温度的变化关系我们可以从图8.4粗略地估计出，处于激发态的扩散原子的散射截面是正常原子的十倍左右，所以其有效电荷数大约等于10Z。
如果我们假设某种金属原子的电阻率与其散射的弹性碰撞截面成正比，也就是假设与其原子偏离平衡位置的平均位移的平方成正比，即<x2>，那么正常晶格原子弹散射截面可以通过爱因斯坦的原子振动模型来进行估算，其中每个振动模式所具有的能量为
式中，mω2为简谐振动的弹簧常数，而m和ω分别为原子质量和原子振动的角频率。
为了得到扩散原子的散射截面，即<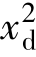
>，我们假设该扩散原子与图8.4（b）所示的临近原子获得了扩散动能ΔHm，该参数独立于温度变量：
那么，将式（8.15）与式（8.14）作比，则得出的就是散射截面的比值：
式（8.16）表明该比值和温度成反比。这个关系式是从一个著名的实验事实所得出的，即通常金属的电阻率在德拜温度（Debye Temperature）以上会随温度呈线性变化。将式（8.16）代入计算Z的公式中，则可以得到 (https://www.chuimin.cn)
在上述等式中，当考虑在面心立方金属中的12个<1 1 0>路径中的给定方向（电子流动的方向）上的平均跳跃的概率时，数值因子1/2被抵消。现在可以通过使用式（8.17）在给定温度下计算Z的值，计算所得出的Z的值和那些金、银、铜、铝、铅的实验测量值吻合得十分好（表8.2）。例如，在480℃下，对于铝（ΔHm＝0.62 eV/原子）的Z的测量值和计算值分别为-30和-25.6。对于金，Z随温度的变化关系如图8.5所示，其计算值与测量值也十分一致。
表8.2 Z测量值和计算值的比较
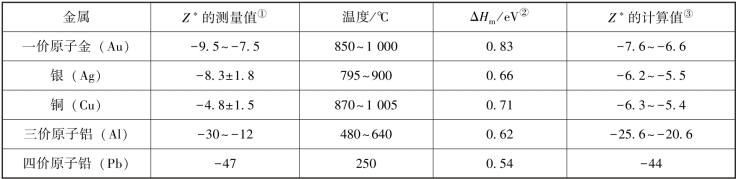
注：①Z的测量值数据来自Huntington（1974），此处忽略了一些无关因素；②ΔHm的数据来自表3.1；③Z的计算值数据由式（8.17）计算得出。
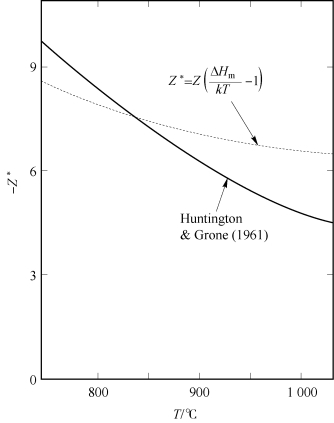
图8.5 金原子的Z随温度的变化关系
我们可以从图8.4（b）粗略地估计出，处于激发态的扩散原子的散射截面是正常原子的十倍左右，所以其有效电荷数大约等于10Z。其中，Z是其名义价电子数，所以对于铜（贵金属）、铝和铅（或锡），我们得到的Z的大小分别为-10、-30和-40。
相关文章
- 详细阅读
-
计算扭转角的方法详细阅读
圆轴扭转时，任意两横截面产生的相对角位移称为扭转角。扭转角φ 是扭转变形的变形度量。GIp 反映了圆轴抵抗扭转变形的能力，称为圆轴的抗扭刚度。图6-20扭转角示意图如果两截面之间的扭矩值T 有变化，或轴的直径或材料不同，则应该分段计算各段的扭转角，然后叠加求代数和。图6-21传动轴的扭矩图计算极惯性矩。......
2025-09-29
-
散热系数的计算方法和影响因素：Nul数、导热详细阅读
在自由对流条件，对流散热系数可按式计算式中 Nul——努基尔数；λ——空气的导热系数；l——空气流过表面的长度。表5-3 公式中长度c、n和长度l的选择对流散热系数α是温度的函数，它随温度而变化。在热分析时，为了与对流散热的形式一致，将辐射散热通过表面散热系数简化为公式所示。因此，外表面的散热系数为α=αcon+αrad......
2025-09-29
-
确定冷却数和特性数的方法与注意事项详细阅读
图7-11T2—K曲线由于冷却塔内气水处于热平衡状态，即有下式成立式中符号同前，则有假设在整个塔内该式成立，则有式中T1、T2分别为进水温度和出水温度。图7-12气水比及冷却数的确定表7-1值选择范围......
2025-09-29
-
剪切的常见计算方法详细阅读
剪切试验试件的受力情况应模拟零件的实际工作情况进行。若以A 表示销钉横截面面积，则应力为τ 与剪切面相切，故为切应力。以上计算是以假设“切应力在剪切面上均匀分布”为基础的，实际上它只是剪切面内的一个“平均切应力”，所以也称为名义切应力。当F 达到Fb 时的切应力称剪切极限应力，记为τb。对于图5-8 所示的剪切试验，剪切极限应力为用τb 除以安全系数n，即得到许用切应力这样，剪切计算的强度条件可表示为......
2025-09-29
-
动态特性计算的方法与实现详细阅读
电磁系统的动态特性的计算必须和电路方程及动铁心运动方程结合起来，同时还要使用电磁机构静态吸力特性。图4-19 螺管式磁脱扣器保护特性的计算采用拍合式脱扣器相同的实验方法，对额定电流为63A螺管式脱扣器样机进行10次测量，测得的平均脱扣时间为6.0ms，然后用本章采用的方法进行计算，得到的脱扣时间为6.5ms，相对误差为5.8%。......
2025-09-29
-
动态应力应变的计算方法优化详细阅读
断路器操作机构的疲劳问题主要是由闭合与分断过程中的动态应力应变引起，因此对断路器操作机构疲劳寿命评估的前提是分合闸过程中零部件动态应力应变的准确计算。动态应力应变的计算基于柔性体的瞬态动力学分析，瞬态动力学分析是用于确定结构在承受任意随时间变化的载荷时的动力学响应的一种方法。常用的瞬态动力学求解方法包括：完全法、缩减法、模态叠加法，本章中柔性体应力应变的计算使用模态叠加法。......
2025-09-29
-
分段计算法：提高运动计算精度的方法详细阅读
分段计算法就是把时间分成一个个小段，在每一个小段时间内，把变加速运动近似地看成是等加速运动来解。为了提高计算精度，我们取时间段初和时间段末的加速度的平均值，作为计算每个时间段速度增量的加速度。图15-5切除故障瞬间的过剩功率图15-6转子摇摆曲线1—稳定；2—不稳定分段计算法的计算精度与所选用的时间段的长短（即步长）有关，Δt太大，固然精度下降；Δt过小，除增加计算量外，也会增加计算过程中的累计误差。......
2025-09-29
相关推荐