图11.5剪切试验中倒装芯片试样的光学照片对电迁移对焊料接头剪切行为的影响进行研究，图11.5所示为倒装芯片键合到有机基板上的组件的光学照片，其中大的白色箭头为施加在芯片上推动芯片的力，并对芯片和电路板间的焊料接头产生剪切力。图11.6所示为第二组施加电迁移的试样断口俯视图的SEM照片。剪切试验中菊花链交替失效的现象表明电迁移通过阴极界面处的孔洞形成弱化了阴极界面，这与拉伸试验的结果类似。......
2023-06-20
电子风力对电迁移现象的影响
【摘要】：是假想电荷数，它所表示的是电子与扩散原子之间动量交换的力的等效效果；eE是电子风力，在良导体中通常它是直接力的十倍左右，在金属的电迁移现象中电子风力的作用要远大于直接力。所以，在电迁移现象中，被增强的原子扩散通量方向通常与电子漂移通量方向一致。换句话说，它将会体验到更大的电子散射作用，以及更大的电子风产生的力的作用，从而将其推向下一个平衡位置，即该原子扩散前空位所在位置。
由Huntington和Grone所提出的作用在扩散原子（离子）上的电场力可以用下面的公式所描述：
式中，e是单个电子的电荷；E是电场强度（E＝ρj，其中ρ是电阻率，j是电流密度）；Z*是电迁移等效电荷数；
可以被认为是，当忽略动态屏蔽效应时，金属中扩散离子的名义价态，它在电场下会产生力的作用；
eE是直接力。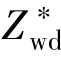
是假想电荷数，它所表示的是电子与扩散原子之间动量交换的力的等效效果；
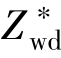eE是电子风力，在良导体中通常它是直接力的十倍左右，在金属的电迁移现象中电子风力的作用要远大于直接力。所以，在电迁移现象中，被增强的原子扩散通量方向通常与电子漂移通量方向一致。
为了理解电子风力的作用，我们在图8.4（a）中描绘了面心立方晶格结构中，一个被涂上阴影的铝原子和相邻空位，在沿<1 1 0>方向交换位置之前的结构示意。它们都有四个最临近的原子，其中包括两个由虚线圆圈所表示的密排面上原子，一个在该阴影原子的顶部，另一个在其底部。如图8.4（b）所示，当该阴影原子向空位的扩散过程进行到一半的时候，该原子便处于激发态，它位于鞍点，并使四个最临近原子产生偏离平衡位置的位移。因为鞍点并不是属于晶格规则周期的一部分，所以在鞍点的原子处于偏离平衡态的位置，并且它相对于正常晶格中的原子，会对电流产生大得多的电阻值。换句话说，它将会体验到更大的电子散射作用，以及更大的电子风产生的力的作用，从而将其推向下一个平衡位置，即该原子扩散前空位所在位置。这样，原子的扩散运动在电子的流动方向上得到了增强。这里我们需要注意，扩散原子不仅在鞍点会受到电子风力的作用，该作用是在从扩散起始到跃迁结束的整个扩散路径中一直存在的。
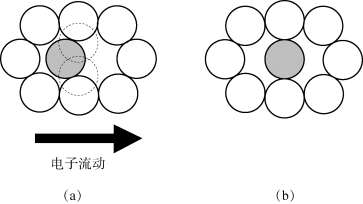
图8.4 电迁移扩散原子示意
（a）在激活之前的状态；（b）在激活之后的状态
为了估算电子风力的大小，Huntington和Grone[1]提出了一种弹道方法（Ballistic Approach）来对电子散射过程进行物理建模。这个物理模型假设性地提出了一种跃迁概率，用于描述由于扩散原子的散射作用，即在单位时间内从一个自由电子态跃迁至另一个自由电子态的可能性。其相互作用力，即单位时间内的动量传输，可以通过对从初始态到最终态的散射电子进行求和以计算得出。下面给出一个简化的推导过程。
在电子与扩散原子的弹性散射过程中，其系统的总动量始终守恒。传输方向上的电子动量的平均变化等于2me<v>，其中me是电子质量，<v>是电子在电流方向下的平均速度。那由于散射而作用在金属离子上面的力为
式中，τcol是相邻的两次碰撞之间的平均时间间隔。平均每秒单位体积内的电子向扩散原子传输的净动量损失为2nme<v>/τcol。那么作用在单个扩散离子上的力为
式中，n是电子密度；Nd是扩散离子密度。那么电子电流密度可写为
将<v>代入式（8.5）和式（8.4），可以得到
式中，ρ＝E/j是导体的总电阻率；ρd＝m/（ne2τcol）是因扩散原子而引起的金属电阻率；E是外加电场强度。
除了电子风力的作用，电场E还会在扩散离子上施加一个直接作用力，其可以写作
式中，
是忽略动态屏蔽效应时金属中扩散离子的名义价态。这样，全部的合力应力为
式中，N是导体中的原子密度，并且使用了n＝NZ的关系式。式（8.8）可以写为
式中，Z*为离子在电迁移中的等效电荷数。
基于电子的弹道散射的电迁移模型是研究电迁移现象的第一个模型，也是最简单的模型。许多研究者进一步对电迁移的理论认识做出了贡献，并影响至今。尽管之后理论认知不断发展完善，但这个由Huntington和Grone所建立的模型，特别是电迁移漂移速度概念的提出，被当作几乎所有基于实验方法研究电迁移现象的理论基石。例如，电迁移的漂移速度可写为
式（8.11）表明，如果我们可以在金属短条上测量出漂移速率（将会在下面8.5节和8.6节中详细讨论）并且知道其扩散系数D，我们就可以计算出Z*。
上述模型表明，有效电荷数可以表示为扩散原子和正常晶格原子的电阻率的函数：
式中，ρ＝m0/（ne2）τ和ρd＝m*/（ne2τd）分别为位于平衡态的晶格原子与扩散原子的电阻率。m0和m*分别为自由电子质量和有效电子质量，并且我们可以假设它们相等。τ和τd为弛豫时间。在面心立方晶格中，沿<1 1 0>方向有12个等效的跃迁路径。对于某一个电流方向，扩散原子的平均比电阻率需要被修正为原值的1/2。通过改写式（8.10），我们可以得到以下关系式：
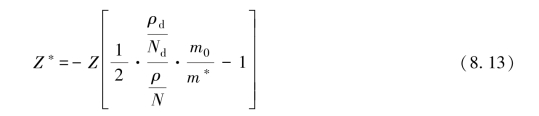
式中，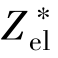
被金属原子的名义价态Z所替换。该公式是Huntington和Grone为了计算电迁移中有效电荷数所得出的。为了计算出Z*，我们需要首先知道该扩散原子的电阻率，或是它与晶格原子的电阻率比值。
有关电子软钎焊连接技术 材料、性能及可靠性的文章
- 详细阅读
-
金属互连中的电迁移现象优化：探析金属互连中的详细阅读
铝薄膜互连线，需要至少在绝对温度达到1/2的熔点时开始产生电迁移现象。换句话讲，如果物质的浓度场是无源场的话，原子和空位的扩散通量将会均匀分布，则在互连线中也不会发生电迁移现象。如果在某个区域中，它们的分布是十分均匀的，则会有电迁移现象的发生，但并不会有电迁移所导致的损伤出现，其本质原因是其场量是无源的。在接下来的内容中，我们将接着分别讨论微观结构、溶质原子和应力对于焊点的电迁移现象的影响作用。......
2023-06-20
-
电迁移对拉伸试验结果的影响探究详细阅读
为了分析阴极界面弱化是否是由电迁移导致的抗拉伸强度减弱的原因，我们分析了有、无电流加载时试样在拉伸试验后的断裂照片，如图11.4所示。图11.4有、无电流加载时试样在拉伸试验后的断裂照片没有电迁移；电迁移96 h；电迁移144 h......
2023-06-20
-
电迁移和热迁移的影响因素与控制方法详细阅读
焦耳热不仅会增加焊料凸点的温度，从而增加电迁移速率，还可能在焊料凸点上产生小的温度差，从而导致热迁移。热迁移将在第12章中讨论。焊料接头中另一个非常独特和重要的电迁移行为是它有两个反应界面。图1.16所示为阴极接触界面处电迁移导致的失效的SEM横截面照片，其中额定电流密度约为2×104 A/cm2，试验温度为100℃。图1.16一组由倒装芯片焊料接头阴极处的电流拥挤造成的14μm厚的金属Cu的UBM层溶解导致的电迁移失效SEM照片......
2023-06-20
-
电迁移对金属间化合物生长的竞争影响详细阅读
然而，在电迁移中应当考虑在阴极、阳极处的金属间化合物间跨越焊料接头的相互作用。为充分理解伴随有阴、阳极间金属间化合物的相互作用时电迁移对金属间化合物竞争性生长的影响，就不能忽略阴极处金属间化合物向焊料的溶解，且必须考虑阳极处金属间化合物的析出。我们有可能可利用这样的试样探究清楚电迁移对三层金属间化合物间竞争性生长的影响。......
2023-06-20
-
电迁移中产生的熵增量对微观结构影响很大详细阅读
作为比较，在电迁移中主要的熵增来源于焦耳热：式中，jem为电流密度；φ为电势。取jem＝104 A/cm2，ρ＝10-5Ω·cm，可得其数量级与400 K温度附近1 000 K/cm温度梯度下的热迁移产生的熵增数量级相同。类似地，电迁移中其他来源的熵增都很小。因为由焦耳热或热传导产生的熵增比原子迁移产生的熵增大几个数量级，可想而知电迁移或热迁移中产生的熵增会大大影响微观结构。......
2023-06-20
-
人口迁移对城乡发展的影响详细阅读
据表中数据显示三类居民都以医疗保险入保率最高，分别占到49.13%、27.86%和90.70%；城—城流动人口和城市户籍人口都以养老保险为第二高的入保率，分别为43.19%和80.74%，而乡—城流动人口则是工伤保险，为22.57%，养老保险只有21%，这么低的养老保险参保率怎么能保证未来的养老。然而城—城流动人口和城市户籍人口的工伤保险参保率也不低，分别占到34.64%和42.63%。......
2023-08-10
-
热迁移现象的原位观察技术详细阅读
据观察，在150℃条件下的电迁移试验中，铅是主要的扩散元素。回流结束后，高铅焊料内会产生Cu3 Sn，但随着锡向热端扩散，Cu3 Sn转变为Cu6 Sn5。在硅侧的整个接触区域内，孔洞和Cu6 Sn5的分布是均匀的。......
2023-06-20
相关推荐