目前，国内外对于单气泡界面传质研究较为深入，而对于高流速、高紊动下的气泡界面传质研究还处于起步阶段。式提供了计算气水两相流中气泡界面传质系数的可靠性，避免了测量气泡上升速度、气泡总面积等所产生的误差，公式所涉及的气泡平均直径和气体体积分数，参考文献［11～13］可供借鉴。......
2023-06-26
界面反应系数的原子模型优化方案
【摘要】：在3.2.4节的动力学分析中，最重要的两个动力学参数是原子扩散率和界面反应控制系数。为了方便比较，在界面反应控制系数中我们提出了一个类似的表达式。图3.11描述了越过Cu6Sn5/Sn界面的活化能，其中ΔGm是穿过界面的迁移活化能，ΔG是反应中或者是Cu6Sn5生长中每一个原子对应的化合物的自由能增益（驱动力），而λ是界面的宽度。图3.11越过Cu6Sn5/Sn界面的活化能式中，p为压力。但由于界面反应过程极其缓慢，因此不太可能考虑分子生长。
在3.2.4节的动力学分析中，最重要的两个动力学参数是原子扩散率和界面反应控制系数。面心立方金属中利用空位的原子扩散理论目前已经比较成熟并出现在多本教科书中。举例来说，扩散率可以表示为
式中，f是相关因子；n是最近邻原子的数目，在面心立方晶格中n＝12；v0是振动的德拜频率；λ是原子与其最近邻空位之间的原子跳跃距离；ΔGm和ΔGf分别是迁移和形成空位的自由能；kT是热能的通常含义。表达式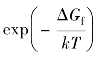
的物理意义是在跳跃原子附近存在空位的概率。
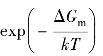的物理意义是原子与最近邻空位之间发生成功跳跃交换的概率。至于相关因子，在面心立方晶格的空位机制中f＝0.87。
为了方便比较，在界面反应控制系数中我们提出了一个类似的表达式。图3.11描述了越过Cu6Sn5/Sn界面的活化能，其中ΔGm是穿过界面的迁移活化能，ΔG是反应中或者是Cu6Sn5生长中每一个原子对应的化合物的自由能增益（驱动力），而λ是界面的宽度。若考虑一维生长，并假定一个单位面积界面前进距离为dx，或一个dx乘以1的体积，那么这一体积内的原子数为
，其中Ω为原子体积。因此获得的总自由能应当为
且应等于这一过程中外力所做的功。
图3.11 越过Cu6Sn5/Sn界面的活化能
式中，p为压力。为了检验ΔG，根据如下的化学反应：
可知化学亲和力
式中，μη是Cu6Sn5化合物分子的化学势，μCu和μSn分别是未反应的Cu和Sn原子的化学势。反应中吉布斯自由能的变化量是
式中，n是反应的程度（单位为摩尔或分子），S、T、V和p都是在热力学中的通常含义。在常温常压下，反应的自由能增加量为
为将驱动力与界面反应的动力学相联系，需要考虑从Sn晶粒穿过界面跳跃到Cu6 Sn5晶粒过程中的Sn的原子通量，有[7]
式中，A2是Cu6Sn5表面每单位面积上原子适配的概率，即一个原子可以附着到Cu6Sn5晶粒上的概率，n1是Sn晶粒上单位面积内即将越过界面的原子数，v1是振动频率。从Cu6 Sn5到Sn的反向通量是
如果ΔG＝0，则两侧处于平衡状态，意味着增长停止。净迁移量为0，则通量相等。因此有
当ΔG<0时，则有净增长运动
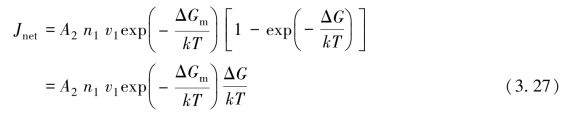
线性化处理过程假定ΔG≪kT。生长速度是
式中，M是迁移率；
＝p[式（3.20）]。
为核查M的单位，可注意到，在爱因斯坦关系的基础上，M＝D/kT，其中D是扩散率，单位为cm2/s。由于A2 n1Ω2和v1的单位分别为cm2和s-1，故可得结果正确。为了比较，代入扩散率
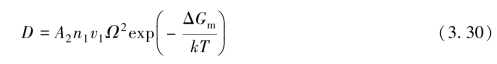
并将其与面心立方晶格中利用空位机理所得的原子扩散率相比较，有
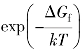的物理意义是可跳跃原子旁边具有空位的概率，所以它类似于式（3.24）中A2中的含义，即Cu6Sn5表面上能够接受Cu原子或Sn原子的位点概率。如果A2＝1，界面动力学过程快，则生长类型为扩散控制型；如果A2<1，界面动力学过程比较缓慢，则生长类型为界面反应控制型。至于相关因子，在面心立方结构的空位机制中f＝0.87，但由于生长过程中，原子离开化合物分子发生反向跳跃或解离跳跃的概率很小，因此在反应生长中可取f≈1。
以上讨论了一个原子接着一个原子的生长过程。由于过程中涉及Cu原子和Sn原子两种原子，故需考虑每个分子的生长，它将涉及6个Cu原子和5个Sn原子。但由于界面反应过程极其缓慢，因此不太可能考虑分子生长。另外，当假设生长方式是一个原子接着一个原子的，则每个原子的自由能增益会小于A/11，其中A是形成Cu6 Sn5分子的化学亲和能。这是由于只有当形成一个完整的Cu6 Sn5分子时，才可获得能量A。若它只是部分形成，则每个原子对应的平均能量应高于A/11。
有关电子软钎焊连接技术 材料、性能及可靠性的文章
- 详细阅读
-
自由界面传质系数的优化方法详细阅读
国内外学者对水气自由表面传质系数给予了很多的兴趣和研究，主要是为了增加水中的溶解氧浓度，迄今都是非饱和复氧研究，其计算方法可分为3种途径［6］：①由水质监测资料按水质模型反算。选择好实验条件，尽可能地排除非大气对水体的复氧作用，这种方法估算的传质系数，仅仅反映了实验河段和当时的水文气象情况，当预测情况发生变化时，如河流修建水库后，所得结果则难以应用；③由公式法估算。......
2023-06-26
-
乘员显控界面设计优化方案详细阅读
在进行乘员显控界面设计时，由于每个显控终端需要为乘员提供的信息显示和操控内容较多，都需要设计不同的界面来分类显示不同类型的信息和操控界面。为了保证所有乘员显控界面风格的一致性，提高界面的可用性，乘员显控界面设计包括框架设计、颜色字体设计及详细设计3个步骤。图4-9一个典型的乘员显控界面......
2023-06-24
-
容许应力和安全系数的优化设计方案详细阅读
在理想情况下，为了保证构件能正常工作，必须使构件在工作时产生的工作应力不超过材料的极限应力。即构件中的最大工作应力不超过某一限值，将极限应力σ0缩小K倍，作为衡量材料承载能力的依据，称为允许应力，用[σ]表示，即式中 K——一个大于1的系数，称为安全系数。安全系数K的确定相当重要又比较复杂。一般工程中规定脆性材料Kb＝2.5～3.0塑性材料或Ks＝1.4～1.7常用材料的许用应力可见表5-2。表5-2常用材料的许用应力......
2023-06-16
-
毁伤增强模型的优化方案详细阅读
图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀，裂纹内气体体积可表述为式中，a为裂纹长度；W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点，爆燃反应冲击波呈球形在跑道各层介质中传播，产生径向压力波，强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中，A为混凝土面层反射系数。......
2023-06-18
-
爆裂毁伤模型优化方案详细阅读
同时，冲击波传入靶体，在径向产生压应力和应变，在切向产生拉应力与应变。由于混凝土靶体材料的抗拉强度远低于抗压强度，因此靶体首先在拉应力作用下发生断裂，形成径向裂纹。气体产物沿裂纹区扩散，导致裂纹进一步扩展，造成本体功能型硬目标结构爆裂毁伤。图6.33混凝土靶爆裂毁伤计算模型混凝土靶体中最终裂纹长度取决于高压气体产物膨胀，而爆燃压力直接取决于进入侵孔内活性材料的质量。......
2023-06-18
-
臭氧接触反应器设备优化方案详细阅读
设计时，应根据臭氧分子在水中的扩散速度和与污染物的反应速度来选择接触反应设备的型式。臭氧接触反应设备，根据臭氧化空气与水的接触方式可分为气泡式、水膜式和水滴式3类。图3-14填料塔3.水滴式臭氧接触反应器喷雾塔是水滴式反应器的一种，如图3-15所示。......
2023-06-19
-
模型参考自适应控制优化方案详细阅读
图3-24所示为设计的模型参考自适应控制方案。那么图3-24 模型参考自适应控制方案可得自然频率wn=30rad/s，调节时间ts≈3.15T1≈0.25s，同时得到参考模型的两个极点-12.6061和-71.3939。为达到控制目标，自适应控制器输出由系统模型定义为Dδ=KT·xδ+θT·r 式中，K=[K1，K2]T和θ分别为闭环系统的反馈增益和前馈增益。上式代入单相并联型APF动态模型式，得定义跟踪误差e=xδ-xm 这里的控制目标为找到一个自适应控制律使跟踪误差e趋近于0。......
2023-06-23
相关推荐