因为在室温或高于室温时生成Cu6 Sn5和Cu3 Sn都会消耗Cu，因此，这两相的生长动力学分析是焊点可靠性的一个重要课题。此外，Cu3 Sn的生长往往伴随着柯肯达尔孔洞的形成。在室温老化过程中，Cu6Sn5层的厚度变化通过卢瑟福背散射获得，且在过程中，并没有检测到Cu3Sn相的形成。综合两者，表明此时存在Sn和Cu混合。实验利用卢瑟福背散射实验装置通过测定Cu6Sn5的减少量来获取Cu6 Sn5相和Cu相之间Cu3 Sn相的生长情况。......
2023-06-20
Cu6Sn5和Cu3Sn连续形成的动力学分析
【摘要】：在Sn和Cu之间的薄膜反应中，Cu6 Sn5和Cu3Sn相相继形成，即Cu6Sn5首先在室温下单独形成，而Cu3 Sn仅在温度达到60℃以上时才会形成。由于在温度超过60℃时Cu6 Sn5和Cu3 Sn可一起形成，因此Cu3 Sn必然能够在60℃以上时形核。Cu6 Sn5的厚度为xβ，其与Cu和Sn的界面的位置分别由xαβ和xβγ表示。由于这个原因，在Cu6Sn5和Cu3 Sn相继生长的过程中，不能假设它们均可成核，且均为扩散控制型生长，从而达到共存状态。
在Sn和Cu之间的薄膜反应中，Cu6 Sn5和Cu3Sn相相继形成，即Cu6Sn5首先在室温下单独形成，而Cu3 Sn仅在温度达到60℃以上时才会形成。众所周知，熔融Sn和Cu之间的润湿反应在更高温度下发生，即Cu6 Sn5和Cu3 Sn可能会同时形成。然而，利用同步辐射研究30 s~4 min的润湿反应时发现，Cu6Sn5和Cu之间存在强结晶取向关系，这表明Cu6 Sn5相在没有Cu3 Sn相生成时已经在Cu上形核，如2.2.1节中所讨论的那样。在经历几分钟更长时间的润湿后，Cu3 Sn形成并与Cu6Sn5同时存在，此外，Cu6 Sn5和Cu之间的取向关系也会受到Cu3Sn生长的影响，见2.2.1节。
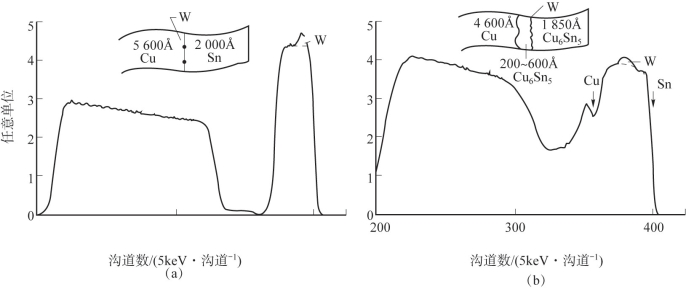
图3.7 Cu6Sn5形成前后W标记信号和双层薄膜Sn/Cu的两组卢瑟福背散射光谱曲线
（a）反应前；（b）反应后
从Sn-Cu二元相图出发，从室温到250℃的温度范围内，这两种相均存在。基于相图或热力学，我们无法解释为什么室温下的固态反应中它们是依次形成而不是同时形成的。相反，我们必须从动力学角度来解释为什么Cu3 Sn不会在室温下形成。从动力学的角度看，要么室温下Cu3 Sn不能形核，要么它即使可以形核也不能长大。而之所以不能长大是因为不能与Cu6 Sn5相的高速生长相竞争。由于在温度超过60℃时Cu6 Sn5和Cu3 Sn可一起形成，因此Cu3 Sn必然能够在60℃以上时形核。形核依赖于过冷度，室温下形核的过冷度比60℃下形核更大，因此很难用室温下没有形核来解释Cu3 Sn没有出现。故需要用另一种原因来解释，即生长过程中Cu3 Sn无法与Cu6 Sn5的快速生长相竞争。
此前，研究者已经研究了Si和金属薄膜发生薄膜反应形成各个金属硅化物的依次生长过程[4]。场效应晶体管器件制备中，在Si上控制形成特定硅化物的单一相形成是制作欧姆接触和栅极非常重要的技术问题。在超大规模集成电路的Si芯片上存在着数百万甚至数十亿个硅化物触点和栅极结构，且这些触点和栅极必须具有相同的物理性质。例如，在触点中不可以出现不同硅化物相的混合物。因此，生产器件要求只能形成单相，而该要求在原则上与热力学原理相悖。因此，这里需要给出动力学机理解释，而非热力学原理。Gosele和Tu[5]研究过单相生长的动力学，他们结合扩散控制生长和界面反应控制生长两个方面提出了一个共存相竞争生长的分层模型。
图3.8所示为两种纯物质之间的层状金属间化合物相的生长，例如Cu6 Sn5相在Cu和Sn之间的生长。Cu、Cu6Sn5和Sn相分别用AαB、AβB和AγB来表示。Cu6 Sn5的厚度为xβ，其与Cu和Sn的界面的位置分别由xαβ和xβγ表示。在界面处，浓度会发生突变。图3.8显示了Cu元素跨界面时的浓度变化。在xβ的扩散控制生长中，假设其界面处的浓度具有平衡值，如图3.8中xβ层内虚线所示。在界面反应控制的生长中，假设其界面处的浓度为非平衡态，如图3.8中实线所示。
考虑图3.8中xβ的层状相为扩散控制生长时，需在一维方向使用菲克第一定律[式（3.1）]。跨越界面和层中的各物质扩散通量如图3.9所示。
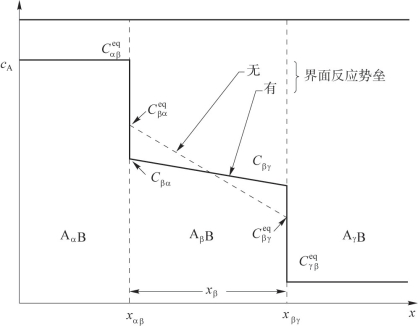
图3.8 两个纯物质之间层状金属间化合物相生长的示意
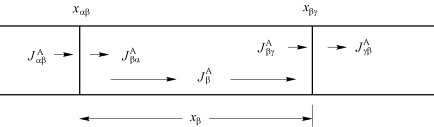
图3.9 界面处和xβ层中的相应通量示意
此外通量方程为
式中，J是原子通量[原子数/（cm2·s）]；D是原子扩散系数（cm2/s）；C是浓度（原子数/cm3）；x是长度（cm），v是移动界面的移动速度（cm/s）。例如，v＝dxαβ/dt表示界面xαβ的移动速度。对于该界面生长，通过考虑进入和离开界面的通量守恒，基于式（3.2）和式（3.1）可得
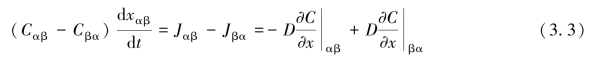
整理后可以得到xαβ界面移动速度的表达式为
由于式（3.4）方括号中浓度梯度未知，因此需进一步通过变换将x和t这两个变量统一到一个变量中，即令C（x，t）＝C（η），其中
由于在扩散控制生长假设下，将界面处浓度当作平衡值来处理，因此界面处的浓度相同，即相对时间和位置而言，Cαβ和Cβα的大小可以假定为常数[6]。故有，因此
在扩散控制过程的界面处，当η是与时间和位置无关的常数时，f（η）＝常数。因此速度方程可写为
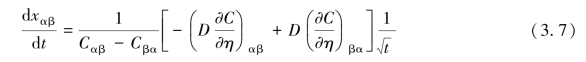
将与时间有关的变量提出方括号后，方括号内的变量将与时间无关。故对上述方程进一步积分，可得
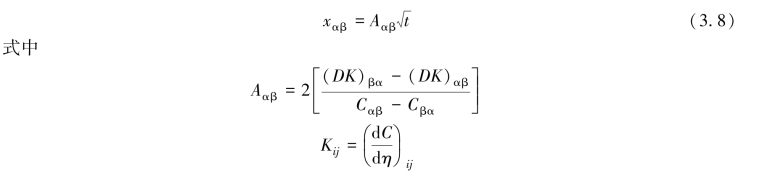
按照类似的方法，可得，另一个界面xβγ为
将两个界面处结果相结合，可得β相的宽度为
这表明β相为生长速率抛物线式，为扩散控制类型的生长。但需注意，上述过程是非常简单的关于层状结构扩散控制的生长过程的推导，或者说对于组分在界面处发生突变的层状生长维持了x2∝t的关系。
扩散控制型层状生长的生长速度与层的厚度成反比，因此在多层结构的竞争生长过程中，该层不会消失，亦不会被消耗掉。当厚度w接近0时，有
生长速率将接近无穷大，即驱动生长的化学势梯度将接近无穷大。因此，在多层结构（例如Cu/Cu3 Sn/Cu6Sn5/Sn结构）中，当Cu3Sn和Cu6Sn5同时存在并处于扩散控制型生长时，它们将保持共存并一起生长。由于这个原因，在Cu6Sn5和Cu3 Sn相继生长的过程中，不能假设它们均可成核，且均为扩散控制型生长，从而达到共存状态。
接下来，再考虑界面反应控制型生长。在这种类型中，生长速率与时间呈线性关系，或者说生长速率是与厚度无关的有限常数。但同时，线性生长不可能一直持续下去；因为当生长到一定厚度时，穿过较厚层状结构的扩散过程将受速率限制，且生长模式将变为扩散控制型，或者说生长过程与时间的关系将从线性转变为抛物线型。
在界面反应控制型的生长中，界面处的浓度将处于非平衡状态，如图3.8所示。β相中的通量
式中，Kβα定义为xαβ界面的界面反应常数，它具有速度量纲（单位cm/s），指Cu原子离开AαB表面的速率。若假设Cu从AαB表面离开时存在滞后效应，则原子浓度Cβα将小于平衡值。另一方面，在xβγ界面，在接受进入的Cu原子时由于同样存在滞后，因此Cu原子浓度Cβγ将大于平衡值。在图3.8中，β相内的虚线表示平衡浓度梯度，实线表示非平衡浓度梯度。β相的生长速度不取决于穿过它的扩散，而是取决于两个界面处发生的界面反应过程。类似这样的层结构动力学分析细节可在文献[5]中找到，这里不再重复。文献中给出的生长速度为
式中，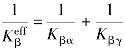
是β相有效的界面反应常数；Kβγ是xβγ界面处的界面反应常数；Gβ是常数；ΔCβ是一个浓度项；Dβ是β相内的互扩散系数。我们定义一个转换厚度，其为
对于一个大的转换厚度而言，或者说
时，即在互扩散系数远大于有效界面反应系数时，可得到
该过程是界面反应控制的，且生长速率是恒定的。
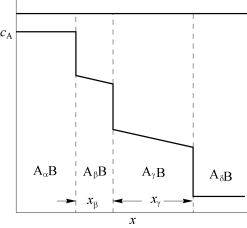
图3.10 四层薄膜结构（Cu/Cu3Sn/Cu6 Sn5/Sn）的原理示意
为便于将扩散控制生长和界面反应控制生长同时应用到薄膜状态下的Cu-Sn反应问题，图3.10中给出了Cu/Cu3 Sn/Cu6 Sn5/Sn四层薄膜结构的示意图。假设Cu3 Sn生长由界面反应控制，且生长速度为v1；Cu6 Sn5生长由扩散控制，且速度为v2。由于v2的大小与层厚成反比，故当层厚较小时，v2量级会很大，故可假设v2≫v1且Cu6Sn5的快速生长可以消耗掉所有的Cu3 Sn。此外，亦可假设这两相都为界面反应控制的生长，其中v2≫v1，同样，生长过程是由Cu6Sn5主导的，因此此时为一个单相生长过程。在3.2.2节图3.4中，已经说明Cu6 Sn5在室温下呈现线性生长特性。
一般来说，偏移速度可以表示为物质的驱动力和界面迁移率的乘积。在薄膜反应中，驱动力是金属间化合物形成的化学亲和能，如Cu6 Sn5的形成能。故而界面反应常数K（速度）的物理意义就是界面迁移率。界面迁移的原子论解释可参见3.2.5节。
实验上，首先制备Cu/Sn双层薄膜试样，并在100℃下老化较短时间以形成Cu/Cu3 Sn/Cu6Sn5/Sn结构，随后在室温下长时间老化以研究Cu3 Sn是会变得更厚，还是会被Cu6 Sn5的生长所消耗。需注意，100℃下的老化时间必须短，这样Cu3 Sn和Cu6 Sn5不会太厚，从而不会变为扩散控制型生长。如果室温老化消耗现有的Cu3 Sn，则表明即使Cu3 Sn可以在室温下形核，它也不能与Cu6 Sn5一起生长，因此由于生长选择，室温下只形成Cu6 Sn5单相。另一方面，如果现有的Cu3 Sn可以生长，或可以与Cu6Sn5共存，那么在Cu和Sn之间的室温反应中没有发现Cu3 Sn相则是因为它无法形核。
有关电子软钎焊连接技术 材料、性能及可靠性的文章
- 详细阅读
- 详细阅读
-
线性连续控制系统策略的分析介绍详细阅读
，bm随时间变化时，系统为时变系统。线性连续控制系统按输入量的变化，又可分为恒值控制系统、随动控制系统及程序控制系统。因此，对于恒值控制系统的分析和设计，主要集中在研究扰动对系统的影响和抗扰动的措施。在恒值控制系统中，输入量可以随生产要求的变化而改变，要求一经整定后，被控量就应随之做出调整。在控制领域，如果被控量为机械位置或其导数，则通常称之为伺服系统。......
2023-06-28
-
直线和圆的位置关系及其连续性详细阅读
1．直线和圆有三种位置关系：________、________、_________．设⊙O的半径为r，圆心到直线l的距离为d，则有：直线l与⊙O相交________；直线l与⊙O相切________；直线l与⊙O相离________．2．直线和圆只有__________________，我们就说直线和圆相切，这条直线叫做圆的切线，这个点叫做________．3．切线的判定：经过半径的外端且____......
2023-07-03
-
螺纹的形成与结构要素分析详细阅读
图7-5加工螺纹2.螺纹的结构要素下面介绍国家标准《螺纹术语》中有关螺纹结构要素的术语。在螺纹牙型上，两相邻牙侧之间的夹角称为牙型角，以α表示。公称直径是代表螺纹尺寸的直径。外螺纹的中径用d2表示，内螺纹的中径用D2表示。在螺纹的诸要素中，螺纹牙型、公称直径和螺距是决定螺纹的最基本要素，凡是这三个要素都符合国家标准规定的螺纹都称为标准螺纹。......
2023-06-28
-
偏心轴动力学输出特性分析详细阅读
在工作室气体合力的作用下推动转子旋转，从而带动偏心轴旋转对外输出扭矩。从图2.38可以看出，偏心轴轴颈的受力也是周期变化的，这是由于离心惯性力在转速不变的情况下是不变的，偏心轴轴颈的受力变化情况只与气体作用力相关。图2.37偏心轴输出扭矩图2.37偏心轴输出扭矩图2.38偏心轴轴颈受力图图2.38偏心轴轴颈受力图......
2023-06-23
-
接触界面扁平型孔洞的动力学分析详细阅读
图9.17所示为扁平型孔洞在接触面上生长的原理示意。由于空位扩散场源所造成的沿界面的横向扩散通量可以写为图9.17扁平型孔洞在接触面上生长的原理示意式中，Dint是界面上的扩散率；b′是电流集聚区域宽度；ΔC为在孔洞顶端或孔洞生长前沿处，空位处于平衡态与高电流密度下的浓度差。假设孔洞的初始宽度是d，Jvoid是孔洞顶端的空位扩散通量。表9.3电迁移中扁平型孔洞生长速率的理论值与试验值之间的对比......
2023-06-20
-
地下连续墙施工的影响和导墙要求详细阅读
地下连续墙施工时对邻近建（构）筑物可能产生的影响。导墙施工接头位置应与地下连续施工接头位置错开。导墙的内墙面应平行于地下连续墙轴线，对轴线距离的最大允许偏差为±10mm；内、外导墙面的净距应为地下连续墙名义厚度加40mm，允许误差为±5mm，墙面应垂直；导墙顶面应水平，全长范围内的高差应小于±10mm，局部高差应小于5mm。挖槽所用时间占地下连续墙工期的1/2，故提高挖槽的效率是缩短工期的关键。地下连续墙挖槽的主要工作为：划分......
2023-08-29
相关推荐