润湿反应和固态老化的动力学分析

2023-06-20 理论教育版权反馈

【摘要】：在200℃的润湿反应中，仅需要几分钟就能形成几微米厚的金属间化合物，但在170℃的固态老化过程中，则需要1 000 h。特别是对于170℃下的固态老化，假设Cu原子通过金属间化合物的扩散激活能为0.8 eV/atom，则Cu的扩散系数约为10-9 cm2/cm。因此，在200℃的润湿反应和170℃的固态老化之间，Cu原子扩散系数存在4个数量级的差异。显然，笋钉状的形貌强烈影响其生长动力学。

我们不去回顾层状金属间化合物的扩散控制和界面反应控制的生长动力学，这里我们考虑润湿反应中笋钉状金属间化合物的生长。图2.26所示为两个笋钉状金属间化合物晶粒的横截面示意图。为了便于分析，我们忽略笋钉状Cu6Sn5和Cu之间非常薄的Cu3Sn。假设Cu不会沿着Cu6 Sn5晶体内部扩散，为了到达熔融焊料中，Cu原子只能通过两个笋钉状Cu6Sn5晶粒之间的凹陷部位扩散。这一部分的Cu原子扩散通量用垂直的箭头表示。由于在熔融焊料中Cu的扩散率约为10-5 cm2/s，因此Cu原子一旦扩散进入熔融焊料就可以迅速到达Cu6 Sn5晶粒前沿，并与Sn原子反应促进Cu6 Sn5生长。同时，笋钉状金属间化合物晶粒之间存在熟化反应，所以两个笋钉状晶粒间也存在Cu原子扩散通量，如水平方向的箭头所示。将Cu原子的这两个扩散通量联合，一个笋钉状金属间化合物晶粒的生长方程如下[23-24]：

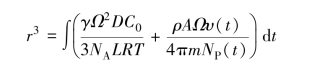
pagenumber_ebook=59,pagenumber_book=45

图2.26　两个相邻的笋钉状金属间化合物的横截面示意

式中，r是笋钉状金属间化合物的晶粒半径；γ是笋钉状金属间化合物的晶粒表面能；Ω是平均原子体积；D是熔融焊料中的原子扩散系数；C0是Cu在熔融焊料中的溶解度；NA是阿伏伽德罗常数；L是与笋钉状金属间化合物晶粒半径和平均间距相关的常数；RT为通常的热力学含义；ρ是Cu的密度；A是焊料/Cu界面的总面积；υ（υ＝dh/dt，其中h和t分别是Cu的厚度和时间）是反应中Cu的消耗速率；m是Cu的原子质量；NP是界面处笋钉状金属间化合物晶粒的总数。我们注意到，这种生长模型中包含了笋钉状金属间化合物晶粒的表面能γ。但在第5章的深入分析中将看到，这种生长现象与表面能无关。方程中，右边的第1项是熟化项，第2项是界面反应项。已发现第1项扩散通量（由图2.26中水平箭头表示）大约是第2项扩散通量（由垂直箭头表示）的10倍。因此，熟化过程决定Cu6Sn5的生长。

由于我们假设Cu在熔融焊料中的扩散非常快，约为10-5 cm2/s数量级，且相邻笋钉状金属间化合物晶粒之间的扩散距离非常短，因此扩散不是决速步骤。然而，Cu的供应不能仅来自晶粒之间凹陷的区域，它们还必须来自笋钉状金属间化合物晶粒的下部区域或晶粒底部区域，这需要Cu沿着笋钉状金属间化合物晶粒与Cu基板之间界面进行横向扩散。我们不得不假设这种界面扩散也非常快的，因为如果这种界面扩散是决速步骤，我们就应该会观察到金属间化合物生长动力学服从规律（而实际为）。另外，假设笋钉状金属间化合物晶粒是半球形的，则笋钉状金属间化合物晶粒表面必须充满原子台阶，因此我们不会有界面反应控制的过程。由于半球沿三维方向生长，生长速率取决于由通道（将在第5章中讨论）所提供Cu的量，因此它是供应限制的笋钉状晶粒生长。我们将其定义为供应控制型生长，而不是扩散控制生长或界面反应控制型生长。

令人惊奇的是，每原子笋钉状晶粒生长的激活能为0.2~0.3 eV/atom，这是激活能非常低的过程，相当于Cu溶解到熔融Sn中的激活能。我们注意到Cu沿着笋钉状金属间化合物晶粒底部界面扩散的激活能可能更高，然而该过程并非决速步骤。

SnPb共晶焊料在Cu基板上的固态老化过程中，我们发现金属间化合物形貌为层状。层状Cu6 Sn5或Cu3 Sn（或两者）的生长激活能约为0.8 eV/atom。因此，固态老化是一个慢得多的动力学过程。另一种比较动力学的方法是比较形成相同量金属间化合物所需的时间。在200℃的润湿反应中，仅需要几分钟就能形成几微米厚的金属间化合物，但在170℃的固态老化过程中，则需要1 000 h。因此，尽管200℃和170℃之间的温度差异仅为30℃，但从时间上讲，润湿反应比固态老化快了4个数量级。

差异的根本原因在于原子的扩散系数。在液态焊料中，Cu原子的扩散系数约为10-5 cm2/s，但在接近其熔点的面心立方结构的固体中，Cu原子扩散系数约10-8 cm2/s。因此，在焊料熔点附近，Cu原子扩散系数差异可达3个数量级。特别是对于170℃下的固态老化，假设Cu原子通过金属间化合物的扩散激活能为0.8 eV/atom，则Cu的扩散系数约为10-9 cm2/cm。因此，在200℃的润湿反应和170℃的固态老化之间，Cu原子扩散系数存在4个数量级的差异。该差异与已发现的x2≈Dt基本关系的时间差有关。

那么在知道固态反应的激活能为0.8 eV/atom后，有这样一个问题：如果在200℃润湿反应中Cu6 Sn5化合物以层状形貌生长，会发生什么？我们考虑到消耗约0.5μm的Cu可以形成一层1μm厚的Cu6 Sn5。我们会发现这需要超过1 000 s的时间，这是由于Cu6Sn5将成为其自身生长的扩散阻挡层。另外，在润湿反应中消耗0.5μm的Cu以形成笋钉状Cu6Sn5，它实际上需要不到1 min的时间。换句话说，金属间化合物形成过程中自由能的增加速率在以笋钉状Cu6 Sn5生长时比以层状生长时快得多。因为当笋钉变得越来越大时，Cu在熔融焊料中的快速扩散在层状生长中没有被利用，所以层状生长速度缓慢。因此，决定金属间化合物形貌为笋钉状的是自由能的变化速率而非自由能的变化值。

显然，笋钉状的形貌强烈影响其生长动力学。由于它必须随着时间增长而变大，笋钉状金属间化合物的半径不能是恒定的。如果晶粒顶部的半径不变，则两个笋钉状金属间化合物晶粒间的凹陷将闭合，那么它们必然变长并成为扩散阻挡层。然而，不是每个笋钉状晶粒的半径都会增大，其中有一些必定会收缩，即发生熟化反应（择优生长）。但是，该熟化过程最终必然会减慢，其原因在于，笋钉状金属间化合物晶粒越大，到达熔融焊料的最短扩散路径（笋钵状晶粒间的凹陷处）的数量越少。我们将在第5章中讨论确定笋钉状金属间化合物晶粒的大小分布，有趣的是它是否服从LSW熟化理论[25-27]。其分布函数是否与时间无关也不清楚。在电子器件的典型润湿反应中，所消耗Cu的厚度小于1μm，因此笋钉状金属间化合物晶粒根本不大。

另一个问题是为什么固态老化中Cu6Sn5不能保持笋钉状形貌。这是由于笋钉状金属间化合物界面比平状界面的面积更大。在润湿反应中，化合物形成能的快速增益可以补偿笋钉状金属间化合物形貌生长所消耗的界面能，但在固态反应中并非如此。第5章中，我们将知道在生长中，笋钉状晶粒的总表面积没变，而总体积在增加。在固态老化过程中，自由能的快速增益消失了，因此为了减少界面能，化合物转变为层状形貌。

润湿反应和固态老化的动力学分析

相关推荐