将粒子群算法应用在生产调度中需要做几下几部分工作： 第一， 将工件加工的顺序编码成为搜索空间中的一个解， 及要建立问题的解和粒子之间的映射关系； 第二， 对算法中的参数进行设置和优化； 第三， 设定适应度函数， 将优化目标和解相关， 可以评价解的优劣。
1. 半导体生产调度问题的编码和计算
假设一个两阶段的半导体生产问题， 加工工件与各阶段和设备的加工能力如表6-1 所示。
表6-1 设备加工单位产品所需单位时间
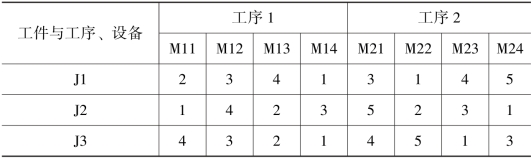
表6-1 给出了一个两阶段半导体的生产系统， 共有3 种工件，每种工件对应两道工序， 每道工序中有四台设备。 每台设备对于工件都有相应的单位加工时间。 表6-2 则是根据表6-1 中设备的对应工件的加工能力的优先级顺序。 优先级顺序按照1＞2＞3＞4 排列。在初始化粒子位置时， 我们可以限定优先水平， 比如小于4 的优先水平的设备才能被选中。 这种方式有助于收缩搜索的空间， 能够改善算法的搜索速度和求解的质量。 比如， 在初始化粒子位置时，M13 的设备不能用于工件J1 的加工。 根据编码的方法， 我们可以给出该问题的某个粒子编码如表6-3 所示。
表6-2 每个工序对应工件的优先水平
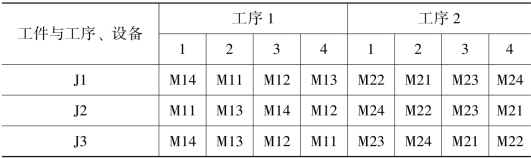
表6-3 某一粒子编码
在粒子算法求解调度问题中， 一个粒子代表一个调度方案。 我们用一个二维的向量表示一个粒子的位置向量。 两个向量在粒子的同一维数上的分量相互对应。 其中Xp[L]的分量代表了工件编号，工件出现的次数代表了所在加工环节的顺序数， 对应的Xm[L]的分量代表了所在加工环节的设备优先排序。 比如表6-3 表示某一粒子编码， 其中第一列代表工件J1 在第一个加工环节的优先排序为2， 及设备M11 上加工； 第五列代表了工件J1 在第二个加工环节的优先排序为3， 及设备M23 上加工。 粒子的维数等于每个工件经过加工环节数量之和。 上例中有三个工件经过两个加工环节， 因此粒子的维数为6。 并且按照加工环节的顺序排列所有位置向量。 例子中前三个位置向量表示第一个加工环节的粒子位置， 后三个向量表示第二个加工环节的粒子位置。 由于半导体生产线的特点， 每个工件必须按照工艺路径顺序经过所有加工环节， 因此粒子在编码的时候， 位置向量一定是从前面的加工环节的设备向后面的加工设备排列的， 对同一工件不允许出现下游加工环节的设备位置排在上游加工环节的设备位置前的。
2. 速度向量和位置向量的计算
速度向量与位置向量相对应， 也是一个二维的向量组， Vp[L]和Vm[L]。 按照式(6-1)可以计算出新种群的粒子速度向量。 再利用公式(6-2)可以计算出Xp[L]和Xm[L]。 在计算初始时刻， 粒子的初始种群和初始速度都是随机产生的。 在计算过程中要注意以下两点：
(1)Xm[L]的取值范围。 由于Xm[L]是表示选用设备所处的优先级， 优先级都是正整数， 并且取值范围是从1 到该生产环节的设备数， 假设为Si， 即取值范围[1， Si]。 在计算Xm[L]的值时，有可能产生小数， 那么对值进行向上取整处理， 如果超出了[1，Si]的范围， 则按取值范围边界进行取值。
(2)关于Xp[L]值的计算。 由于Xp[L]代表了工件所处的加工环节的位置， 因此Xp[L]值是不会改变的， 但是在同一个生产环节段是可以交换位置的。 位置的先后也是调度方案中执行生产的先后。 图6-3 表示了Xp[L]的计算交换位置的方法。
通过对粒子位置向量和速度向量的计算后， 就可以得到新的粒子， 该粒子也是搜索空间上的解。
3. 半导体生产调度模型中的参数设置
在式(6-1)中， 惯性权重w 是影响整个算法搜索性能的重要参数。w 取较大值可以有助于粒子向新的搜索空间飞行； w 取较小的值， 则有助于粒子提高搜索精度， 在局部获得最优解。 因此， 本书采用式(6-3)对w 进行自适应的变化， 将w 的值从相对较大的值线性地减小到较小值。 这样有助于算法在开始阶段具有很强的全局搜索能力， 随着算法迭代次数的增加， 当锁定全局最优解可能出现的区域后，w 的值也逐渐减小， 最后使得算法可以在锁定的区域内仔细搜索。
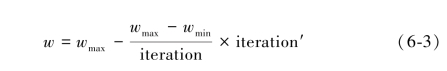
式(6-3)中，wmax 是惯性权重的最大值，wmin 是惯性权重的最小值； iteration 是迭代次数的总代数， iteration′是当前的迭代次数。随着迭代次数的增加， 惯性权重的值也会线性地减小， 直到减小到最小值。
除了惯性权重外， 还有加速度常数r1 和r2， 这两个常数可以按照以往的经验取2。 但是这样仍然不能保证每次计算出的速度值不会过大， 如果速度值过大， 会使得粒子突然飞过问题空间， 最终不能获得最优解。 因此可以对速度的取值限定一个取值空间， 当超过取值空间后， 速度取边界值。 速度是一个矢量， 可以取负。 假定给定速度的取值空间为[-Vmax， +Vmax]。
适应度函数是作为评价粒子(解)优劣的有效手段。 在生产调度中， 通常存在着多个目标， 将多目标转换成单目标， 设定总的目标(评价)函数：
将评价函数f： S →R+ 表示对粒子评价的适应度， 将目标函数值映射成为适应度值。 在判定粒子优劣性时， 适应度值较小的粒子作为更优秀的解而保留下来。
4. 算法流程
粒子算法整个流程如下：
(1)对模型进行编码， 设定种群规模、 算法迭代次数、 参数wmax、 wmin、 r1 和r2 的值。
(2)设定适应度函数f。
(3)另迭代次数为0， 根据初始化粒子群的约束， 随机产生初始化粒子编码。
(4)利用速度和位置的计算公式， 更新粒子的位置和速度， 产生新一代种群， 同时在计算过程中， 比较当前位置和速度与gbest和pbest 的值， 更新gbest 和pbest 值。
(5)对新一代种群作适应度判定， 如果新一代种群优于当前最好种群， 那么用新一代种群替代当前最优种群， 否则， 当前最优种群保持不变。
(6)判断是否达到迭代最大次数。 如果没有达到迭代最大次数， 则跳转至(4)； 如果达到， 则把当前最优的种群作为解输出。
粒子算法可以适合大规模的调度研究， 并且具有搜索解性能强的特点。 很适合应用在半导体生产这种多品种、 多设备、 多生产环节的生产调度中。
有关半导体封装测试制造系统运行优化理论与技术的文章
混沌粒子群优化算法的基本思想是采用混沌序列初始化粒子的位置和速度,先对当前粒子群体中的最优粒子进行混沌寻优,然后把混沌寻优的结果随机替换粒子群体中的一个粒子。,z1N),根据式(4-6)得到N个向量z1,z2,…如果粒子适应度优于全局极值gbest,则将gbest设置为新位置。则混沌粒子群优化算法的流程为:初始化,设置最大允许迭代次数或适应误差限,以及CPSO算法的参数惯性权值和学习因子。,PgD)进行混沌优化:将Pgi(i=1,2,…计算其适应值,得到性能最好的可行解pb。......
2023-06-23
粒子群优化算法的基本思想：PSO中每个优化问题的潜在解是搜索所在空间中的一个粒子，所有的粒子都会有一个对应的函数值来衡量每个粒子解的优越程度，每个粒子还会有一个对应的速度来决定自身飞翔的距离和方法，最终可以实现从全局域内搜索到最优解的目的。......
2023-06-29
粒子群优化算法,是Eberhart和Kennedy[118]提出的一种基于群体智能的优化算法,它是受鸟群和鱼群群体运动的行为方式启发而得到的。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。......
2023-06-23
在Step3中，对冲突的任务进行重调度，为避免冲突的传递和保证算法的效率，重调度的执行深度设置为1，即只对冲突任务执行一次直接调度操作，而不继续进行间接调度操作。在Step3中，冲突任务被替换后若能重新调度，则将执行“整传插入操作”或“续传插入操作”，分别定义为“移动整传操作”或“移动续传操作”；若不能重新调度，则被删除，定义为“删除替换操作”。......
2023-07-02
半导体封装测试企业由于其生产规模较大， 相比其他传统的生产加工企业， 存在多地域分布建厂的情况。生产计划与调度对封装测试生产来讲， 是上下游的依赖关系，生产计划的制订， 决定了周计划产品需求数量， 而这种产品数量初分配， 在某种意义上决定了生产调度的大方向。......
2023-06-20
分别是拒绝策略、 修复策略、 改变遗传算子策略和惩罚策略。本书采用改变遗传算子的策略， 用分组交叉的算子来实现个体的交叉， 这样， 不仅易于实现， 而且不会产生非法染色体。如图6-1 所示：图6-1交叉算子遗传算法是群体进化的一种方法， 其最大优势在于同时使用多个点的搜索信息， 在各种方案之间进行选择、 交叉、 变异等运算。图6-2遗传算法实施流程图......
2023-06-20
粒子群算法的优势在于它的算法简单、 易于实现， 可调参数少， 收敛速度快、 求解快， 可以用于大规模的优化模型中； 基于记忆的特点， 可以对以往产生的最优位置进行保存。公式(6-2)表示了粒子的位置是由上个时刻位置与上个时刻粒子的运动所共同影响的。在粒子群算法的整个过程中， 惯性权重w、 r1、 r2 和最大速度Vmax 对算法的搜索能力和性能影响很大。......
2023-06-20
9.4.5.2调度优化性能分别以32，64，80，100个任务量的仿真场景进行计算，对于每个场景进行100次仿真优化，优化结果取均值与标准遗传算法的优化结果进行比较，比较结果如表9-5所示。......
2023-07-02
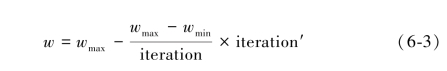
相关推荐