从稳定性角度探讨纳什平衡

2023-06-20 理论教育版权反馈

【摘要】：在均衡问题上， J. Nash 首先证明了博弈均衡解的存在性，在纳什平衡理论的基础上，泽尔腾和海萨尼将Nash 均衡动态化。在SFGDD 协商机制的稳定性问题上，本节运用对策论中的纳什平衡理论寻求多Agent 系统的协商平衡。纳什平衡定义为：对于博弈组合G ＝{S1， …由此可见，纳什均衡的存在性是纳什均衡概念最重要的性质。这也就是纳什均衡概念及纳什均衡存在性定理是博弈中最主要的理论的原因之所在。

因为在半导体封装测试过程中，订单的满足和库存(成品、半成品和在制品)管理上存在相互的冲突和制约，因此需要寻找到一个平衡点，实现订单Agent 和调度Agent 之间的平衡，并且这种平衡必须是稳定的。在前面所建立的协商机制中，将基于对策论的二人非零和对策作为SFGDD 模型的协商机制。均衡问题是对策论的主要研究问题之一，均衡意指对策局势中的相关变量处于稳定状态。在均衡问题上， J. Nash 首先证明了博弈均衡解的存在性，在纳什平衡理论的基础上，泽尔腾和海萨尼将Nash 均衡动态化。在SFGDD 协商机制的稳定性问题上，本节运用对策论中的纳什平衡理论寻求多Agent 系统的协商平衡。

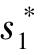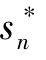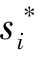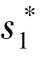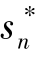纳什平衡定义为：对于博弈组合G ＝{S1， …， Sn； u1， …，un}，如果在由每个博弈方的一个策略所组成的策略组合( pagenumber_ebook=105,pagenumber_book=96 ， …， ) 中，任一博弈方i 的策略，都是应对其他博弈方策略组合的最佳策略，也即对任意sij ∈Si 都成立，则称(， …， ) 为博弈G 的一个“纳什均衡”(Nash Equilibrium)。该定义可以理解为任意一个si 替换 pagenumber_ebook=105,pagenumber_book=96 都不可能让策略集S 效用更大，即整体达到稳态平衡。

纳什在其1950 年的论文中，提出了“纳什均衡点”(Nash Equilibrium Point)的纳什均衡概念，并且证明了策略意义上的纳什均衡是普遍存在的。

纳什定理1(Nash 1950)：在一个有n 个博弈方的标准博弈G ＝{S1， …， Sn； u1， …， un} 中，如果n 是有限的，并且Si 都是有限集(对i ＝1， …， n)，则该博弈至少存在一个纳什均衡点，均衡可能包含混合策略。

该定理可以运用布鲁威尔的不动点定理进行证明，因为纳什均衡从数学的角度来看就是一个不动点的概念。

布鲁威尔的不动点定理数学证明比较复杂，但是具有较强的几何直观性。

布鲁威尔不动点定理：设S ⊂Rn 是一个非空的有界的闭且凸的集合。设f： S →S 是一个连续映射。那么，在S 中至少存在一个f 的不动点，这便是至少存在一个X∗∈S，使得X∗＝f(X∗)。

纳什定理保证了相当广泛类型的博弈中均衡策略的存在性，意味着纳什均衡分析在我们所遇到的大多数博弈问题中，都是一种基本的分析方法。正是因为这一普遍存在性价值，纳什均衡是博弈结果的“一致预测”的性质才有意义，纳什均衡这一概念才会成为分析博弈和预测博弈结果的中心概念和基本出发点。否则，如果多数博弈不存在纳什均衡，那么纳什均衡分析的价值就非常有限。由此可见，纳什均衡的存在性是纳什均衡概念最重要的性质。这也就是纳什均衡概念及纳什均衡存在性定理是博弈中最主要的理论的原因之所在。

在半导体封装测试生产过程中，生产调度需要协同订单的动态变化，在满足订单需求的同时，需要优化半成品、成品、在制品的库存。在基于对策论的协商机制中，订单Agent 和调度Agent 博弈双方存在着此消彼长的相互矛盾，库存量越高，订单相应被满足的可能性越大，但是高库存会带来生产调度的复杂性和成本的显著上升，需要在双方的协商中寻找到一个均衡点，满足彼此赢得函数的最佳值，进行多目标寻优，并达到稳态平衡，因此采用纳什平衡理论来寻求双方博弈过程中的最佳策略。

从稳定性角度探讨纳什平衡

相关推荐