表8.4折弯机外负载和液压缸工作压力运动分析根据给定条件可知:空载快速下降行程180 mm,速度23 mm/s;慢速折弯行程20 mm,其中在开始15 mm 的初压段等速运动,速度为12 mm/s,最后5 mm 的终压段速度均匀地减至零;快速回程以53 mm/s 的速度上升。图8.4折弯机负载循环图图8.5折弯机速度循环图......
2023-06-18
分析平面运动刚体内各点速度
【摘要】：实际分析中，总是以运动已知的点作为基点。平面图形绕基点转动的角速度和角加速度与基点位置无关。这称为“平面运动的速度合成法”或“基点法”。这是确定刚体平面运动图形内任意点速度的基本方法。
可以证明：刚体的平面运动（绝对运动）包含了随基点的平动（牵连运动）和相对绕基点转动（相对运动）这两种基本运动；或者说刚体的平面运动由刚体随基点的平动和相对绕基点的转动复合而成。
关于基点的选择可以得出以下重要结论：
平面图形的平动速度和平动加速度（即牵连速度和牵连加速度）与基点位置有关。实际分析中，总是以运动已知的点作为基点。
（1）平面图形绕基点转动的角速度和角加速度（即相对运动的加速度和角加速度）与基点位置无关。
（2）任意瞬时平面图形绕其平面内任意点转动的角速度和角加速度都相同，又称为平面图形的角速度和角加速度或平面运动刚体的角速度和角加速度。实际分析中，不必指明对于哪一基点。
图10-17（a）中所示滚动的车轮做平面运动，车轮A 点的速度为vA，绕A 点转动的角速度为ω，试求，车轮上的任一点B 的速度vB。
vB（绝对速度）=vA（牵连速度）+vBA（相对速度）
车轮A 点的速度vA 已知，所有选取A 点为基点，则车轮的牵动运动是随基点的平动，B点的牵连速度ve 就等于基点A 的速度vA，即ve=vA，如图10.17（b）所示；车轮的相对运动是绕基点转动，B 点的相对速度vr 就等于B 点以AB 为半径，绕基点A 转动的速度vAB，即vr=vBA，其大小为vAB=AB×ω，方向⊥AB，指向与角速度ω 转向一致，如图10.17（c）所示。
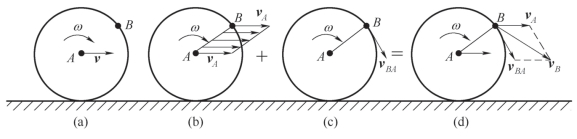
图10-17 滚动的车轮
应用速度合成定理，如图10-17（d）所示，B 点的绝对速度为
式（10-22）表明：平面图形内任意点的速度，等于基点的速度与绕基点转动产生的线速度之矢量和。这称为“平面运动的速度合成法”或“基点法”。这是确定刚体平面运动图形内任意点速度的基本方法。
有关工程力学（第2版）的文章
- 详细阅读
-
点速度合成定理及应用详细阅读
应该指出，式中，没有对牵连运动作任何限制，因此，速度合成定理对于任何形式的牵连运动都适用。因此，动点在某一瞬时的牵连速度和加速度，实际上是动坐标系上与动点相重合的那一点，即牵连点的速度和加速度。应用速度合成定理：式中ve，vr——分速度；va——合速度。由图中的几何关系，求得绝对速度的大小为......
2023-06-19
-
点、直线、平面的投影简介详细阅读
2-19一等腰直角△ABC，AC为斜边，顶点B在直线NC上，完成其两面投影。2-20已知菱形ABCD的对角线BD的投影和另一对角线端点的水平面投影a，试完成菱形的投影图。2-25完成下列平面图形的第三投影，并求作出属于平面上的点K的另两个投影，并填空。2-26作图判断点A或直线AB是否属于给定的平面。2-34过已知点A作一直线AB，使其平行于已知平面△DEF。2-36求作直线与平面的交点K，并判断可见性。......
2023-06-15
-
音乐活动设计中各速度的计算详细阅读
现代音乐常以“拍每分钟”作为速度的单位。以附图2-1中的数字104为例，表示以四分音符为一拍，每分钟的拍数为104。所以建议教师在开展音乐活动前打开节拍器对速度进行核实。附图2-1显示的速度范围40—208，其计算方式分别是：①40—60的速度区间内，间隔为2。④120-144的速度区间内，间隔为6，所以这个区间内的速度依次是126、132、138、144。但是在幼儿园音乐教育阶段还应以节拍器上的规范速度为主。......
2023-08-16
-
点、直线、平面的正投影特点详细阅读
图2-9正投影的类似性2.2.1.4重合性两个或两个以上的点、线、面具有同一投影时，称为重合，这种投影性质称为正投影的重合性，如图2-10所示。......
2023-06-22
-
平面连杆机构的运动学分析与优化设计详细阅读
任务要求绘制缝纫机踏板机构的运动简图，分析其组成及运动特点。图2.6双曲柄机构图2.7惯性筛双曲柄机构中，当两曲柄长度相等，连杆与机架的长度也相等时，称为平行双曲柄机构或平行四边形机构。图2.9公共汽车车门启闭机构双摇杆机构铰链四杆机构的两个连架杆均为摇杆时，称为双摇杆机构，如图2.10所示。......
2023-06-30
-
点、直线、平面的投影学习指南详细阅读
本章的地位及特点本章介绍正投影图的基本知识，包括点的投影规律、各种位置直线的投影特性及不同相对位置两直线的投影特性、各种位置平面投影特性，以及点、线、面之间的从属关系，直线与平面的平行和相交关系等。正投影是平行投影的特例，因此平行投影的基本性质是建立正投影的基础。第2章介绍了工程中表示物体的常用方法，本章从点的投影开始，逐步深入地讨论用于表达物体正投影的方法。......
2023-06-28
-
平面内点与直线的关系详细阅读
图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2023-06-22
相关推荐