从前面几节的讨论中可以看到,电力系统受扰动后发电机之间相对运动的特性,表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性,必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节,将导出适合电力系统稳定计算用的发电机转子运动方程。发电机转子运动方程,是电力系统稳定分析计算中最基本的方程。......
2025-09-29
图10-16(a)中所示的一般刚体,平面Ⅰ为某一固定平面,作平面Ⅱ平行于平面Ⅰ,并与刚体相交。刚体上与平面Ⅱ相交的部分,称为“平面图形”,用S 表示。根据平面运动的特征,当刚体做平面运动时,平面图形S 上各点始终在平面Ⅱ运动。如果在平面运动的刚体上作平面图形S 的垂线,则直线上所有点的运动都与垂线和平面图形的交点[例如图10-16(a)中的M点] 的运动完全相同,因此,研究做平面运动的刚体上各点的运动,只要研究平面图形S 内各点在平面Ⅱ的运动即可,从而将刚体的平面运动简化为平面图形S 在其自身平面内的运动。
为研究平面图形S 在其自身平面内的运动,在此平面内建立静坐标系Oxy。如图10-16所示。确定平面图形S 在Oxy 坐标系中的位置,只需确定图形上的任意直线段[例如图10-16(b)中的O′M 直线段] 的位置。因为图形上任何第三点至这直线两端的距离都保持不变,故当直线段的位置确定之后,其余各点的位置便随之确定。
直线段的位置由它任一端点的坐标以及直线段与Ox 轴的夹角所确定。确定线段位置的端点(例如O′)称为“基点”。
综上所述,只要确定了平面图形S 上的任意直线段的任一端点坐标,以及直线段与Ox轴的夹角φ,也就确定了平面图形S 上任意点的位置,因此也就确定了做平面运动刚体上任意点的位置。
基点坐标![]() 以及过基点的线段与Ox 轴的夹角φ,都可表示成时间的单值连续函数。(https://www.chuimin.cn)
以及过基点的线段与Ox 轴的夹角φ,都可表示成时间的单值连续函数。(https://www.chuimin.cn)

式(10-21)称为“刚体平面运动方程”。
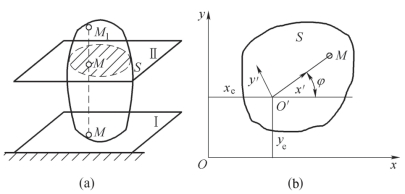
图10-16 刚体的平面运动
相关文章

从前面几节的讨论中可以看到,电力系统受扰动后发电机之间相对运动的特性,表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性,必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节,将导出适合电力系统稳定计算用的发电机转子运动方程。发电机转子运动方程,是电力系统稳定分析计算中最基本的方程。......
2025-09-29

减小扩散边界层厚度是提高染色速率的重要途径之一,它不仅可加快染料到达纤维表面的速度,还可以使扩散边界层的厚度更趋于均匀,使染料能够均匀吸附上染。......
2025-09-29

原则上,正常生产过程中的任何中断都属于特殊情况。如果系统制造商不能提供降低中断频率和提高持续时间的策略,甚至可能会导致废弃生产线。例如,系统中输入的数据可用于控制产品质量和优化系统,从而有助于减少中断。在调试阶段,这些数据有助于缩短优化时间;在运行阶段,它有助于加快解决方案或完全避免中断。......
2025-09-29

三相异步电动机的运动方程为式中,J为机组的转动惯量;TL为电动机负载转矩。以上磁链方程[见式(4.9)]、电压方程[见式]、转矩方程[见式]和运动方程[见式]组成了三相异步电动机的动态数学模型。三相异步电动机的动态数学模型是复杂的,该模型的特点如下:1)多变量。综上所述,三相异步电动机的数学模型是一个多变量、强耦合、非线性和高阶的系统,直接用该模型很难整理得出三相异步电动机的控制规律。......
2025-09-29

图4.28运动装置的选择具有主要功能性组件的动力装置通常为简单的调节控制元件,如气缸或简单的旋转装置。主要功能可变的运动装置可进一步分为手动控制和程序控制的动力装置。它们用于在对人类有直接风险的情况下执行人类运动,或用于增强人类能力。图4.29显示了空间中的运动由不同的动力学阶段组成,这些阶段可能会影响机械手,如前所述。图4.29用不同颜色标记的加减速运动轨迹在传感器对运动序列的影响方面,近年来取得了重大进展。......
2025-09-29

冷却塔中传质和传热同时进行,冷却塔热力计算的方法目前国内外用得较多的是焓差法,这里主要介绍焓差法。a/kX=为Lewis比例系数,利用其上式可进一步简化写成:以容积传质系数kXVkg/代替kXa,填料塔微元体积dV代替Fdz,得和分别为饱和空气与微元内空气的焓,是冷却的推动力,式简称焓差方程,为冷却塔计算的基本方程式。......
2025-09-29

图6-30 采用蓄能器的快速运动回路1—液压泵 2—溢流阀 3—单向阀 4—蓄能器 5—换向阀 6—液压缸图6-31 双泵供油快速运动回路1—大流量泵 2—小流量泵 3—外控式顺序阀 4—单向阀 5—溢流阀......
2025-09-29
相关推荐