深入探讨点的合成运动概念

2025-09-29 理论教育版权反馈

【摘要】：显而易见，在不同的参考物体上所观察的物体运动是不相同的。显然，牵连运动的类型与刚体运动类型一致。点或刚体的绝对运动是它们相对于动坐标系的相对运动与动坐标系相对于静坐标系的牵连运动的合成结果。研究运动的分析和合成问题，首先要选择好合适的静坐标系和动坐标系，然后分清什么是绝对运动、相对运动和牵连运动；最后分析各种运动的速度和加速度。

前面研究点和刚体的基本运动时，都是以固结在地球表面的坐标系作为参考系的，所涉及的点的运动或刚体的运动，只要相对于这一个坐标系，即可完全被描述。

但在工程问题中，只相对于一个坐标系，很难完整地描述物体的运动。这时往往需要相对于两个不同的坐标系，研究同一物体的运动。两个坐标系中，一个是固定的，另一个则相对于固定坐标系作一定的运动。当然，同一物体相对于这两个坐标系的运动是不同的，但这两种不同的运动之间又存在一定的关系。

如果相对于固定坐标系的运动坐标系选择得适当，则有可能将比较复杂的运动分解为两个简单的运动，从而使问题大大简化。这在理论分析和工程应用上都具有重要的意义。

（1）相对运动与绝对运动。

固结于相对静止物体（一般固结于地球上）的坐标系，称为“静坐标系”，相对于静坐标系有一定运动的坐标系，称为“动坐标系”。动坐标系一般固结于运动物体上。

点或刚体相对于静坐标系的运动，称为“绝对运动”；相对于动坐标系的运动，称为“相对运动”。相对于两种坐标系中点的运动轨迹称为“绝对轨迹”与“相对轨迹”。

以图10-13 中所示的桥式起重机提升重物为例。起重机上部的行走小车A，在从左向右的行进过程中，小车上的卷扬机使重物向上运动。设瞬时t，小车处于位置A。重物（可视为动点）位于M 处。在另一瞬时t+Δt，小车前进到位置A′，重物在提升的过程中运动到达M′处。相对地面而言（即观察者位于地面上），重物沿轨迹MM′从M 点运动到M′点，但相对于小车而言（即观察者位于小车上），重物则在铅直方向运动轨迹从M 点运动到M1 点。显而易见，在不同的参考物体上所观察的物体运动是不相同的。(https://www.chuimin.cn)

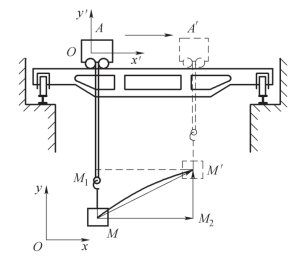
pagenumber_ebook=185,pagenumber_book=176

图10-13　桥式起重机

为了确切地描述上述运动，需要建立不同的坐标系。对于一般情形，工程上通常把静坐标系固结于地面，用Oxy 表示，把运动坐标系固结于运动物体，用O′x′y′表示。

对于图10-13 中的重物，它在Oxy 坐标中的运动，即沿MM′的运动为绝对运动，而在O′x′y′坐标中的运动，即沿铅直方向的运动，则为相对运动。

（2）牵连运动。

通过对起吊重物的运动分析，可以看出，当小车不动、仅重物向上移动时，观察者在地面上和小车上所观察到的重物运动都是垂直向上的直线运动。这时，重物的相对运动与绝对运动一致。因此，重物的相对运动与绝对运动的差异是由小车（即动坐标O′x′y′）运动引起的。因为重物一方面相对于小车做垂直向上的运动，另一方面又被小车牵连在一起做水平方向向右的运动。前者为相对运动；后者则称为“牵连运动”。重物的绝对运动则是这两种运动合成的结果。

通常，将运动物体作为动参考体，并把运动坐标固结在动参考体上。我们把运动坐标系相对于静坐标系的运动，定义为“牵连运动”。显然，牵连运动的类型与刚体运动类型一致。点或刚体的绝对运动是它们相对于动坐标系的相对运动与动坐标系相对于静坐标系的牵连运动的合成结果。研究运动的分析和合成问题，首先要选择好合适的静坐标系和动坐标系，然后分清什么是绝对运动、相对运动和牵连运动；最后分析各种运动的速度和加速度。

深入探讨点的合成运动概念

相关推荐