为了降低梯级链与梯级轮啮合时的噪声,梯级轮的轮齿具有消声装置。这种张紧装置通过张紧架上的链轮直接对梯级链进行张紧,又称为滚动式张紧装置,具有张紧作用稳定的优点。张紧力来自尾部的弹簧,调节弹簧被压缩量即可调节对梯级链的张紧力。梯级链张紧装置整体工作寿命也应按不小于140000h设计。......
2025-09-29
电动机转子的运动、机器中齿轮的运动、钟表指针的运动等,都是定轴转动的实例。分析它们运动的共同特性,可得到刚体绕定轴转动的定义:刚体运动时,其内有一直线始终保持不动,而这条直线以外的各点都绕此直线以点到该直线的垂直距离为半径做圆周运动。刚体的这种运动称为刚体绕定轴转动,简称转动。刚体内固定不动的直线称为转动轴。
(1)转动方程。
描述刚体转动时,首先需要确定刚体在转动过程中任意瞬时的位置。为此,可通过转动轴Z 取Ⅰ、Ⅱ平面[图10-9(a)]。其中Ⅰ平面与地面固定在一起,为一固定平面;Ⅱ平面与刚体连接在一起,随同刚体一起转动,为一动平面。这样,刚体在任意瞬时位置,可用动平面Ⅱ与固定平面Ⅰ之间的夹角φ 来确定[图10-9(b)]。φ 称为转角,单位用弧度(rad)。φ 为代数量,并规定刚体按逆时针方向转动时,转角φ 取正值;反之取负值。显然,当转角φ 已知时,刚体的位置也随之确定。刚体转动时,转角φ 随时间t 而变化,且转角φ是时间t 的单值连续函数,即
![]()
式(10-10)称为刚体转动的转动方程。
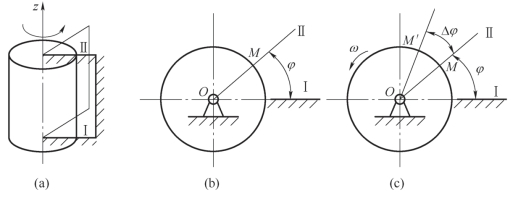
图10-9 刚体绕定轴转动
(2)角速度和角加速度。
角速度是描述刚体转动快慢的物理量。设刚体在瞬时t 的转角为φ,经过Δφ 之后,即在瞬时t+Δt,刚体的转角为φ+Δφ [图10-9(c)]。在时间Δt 内,转角的增量为Δφ。转角增量Δφ 与对应时间间隔的比值称为刚体在Δt 时间内的平均角速度,用ωc 表示,即
![]()
当Δt→0 时,平均角速度ωc 所趋近的极限值就是刚体在瞬时t 的角速度,用ω 表示。即

上式表明,刚体绕定轴转动的角速度等于转角对时间的一阶导数。角速度的正负号表明刚体的转动方向,若![]() ,逆时针转动,表明ω 的转向与转角φ 正向一致;反之,
,逆时针转动,表明ω 的转向与转角φ 正向一致;反之,![]() ,顺时针转动,表明ω 的转向与转角φ 负向一致。因此,角速度的正负号决定了刚体的转向。角速度ω 是代数量。
,顺时针转动,表明ω 的转向与转角φ 负向一致。因此,角速度的正负号决定了刚体的转向。角速度ω 是代数量。
角速度的单位为弧度/秒(rad/s)。在工程上常用转速表示转动的快慢,转速用N 表示,单位为转/分(r/min 或rpm)。N 与ω 的关系是
![]()
角加速度是描述刚体转动角速度变化快慢的物理量。设在瞬时t,刚体的角速度为ω,在瞬时t+Δt,刚体的角速度为ω+Δω,即在Δt 时间间隔内,刚体的角速度增量为Δω,得刚体在瞬时t 的角速度(简称角加速度),用ε 表示为
![]()
上式表明,刚体饶定轴转动的角加速度等于角速度对时间的一阶导数,或转角对时间的二阶导数。角加速度的单位为弧度/平方秒(rad/s2)。如果导数![]() 表示ε 的转向与φ 的正向一致,是逆时针方向;反之,如导数
表示ε 的转向与φ 的正向一致,是逆时针方向;反之,如导数![]() ,表示ε 的转向与φ 的负向一致,是顺时针方向。与角速度情况一样,角加速度也是代数量。但须注意,角加速度正、负的意义,要同角速度正、负联系起来看,和点的运动的v、a 相似,当ω、ε 同号时,表示刚体加速转动;当ω、ε 异号时,表示刚体做减速转动。
,表示ε 的转向与φ 的负向一致,是顺时针方向。与角速度情况一样,角加速度也是代数量。但须注意,角加速度正、负的意义,要同角速度正、负联系起来看,和点的运动的v、a 相似,当ω、ε 同号时,表示刚体加速转动;当ω、ε 异号时,表示刚体做减速转动。
案例10-3 电动机主轴的转动方程为φ=2t2(φ 的单位为rad,t 的单位为s)试计算当t=2 s时,主轴的角速度和角加速度。分析:已知电动机主轴的转动方程为
![]()
转角对时间的一阶导数就等于角速度
![]()
角速度对时间的一阶导数就等于角加速度
![]()
将t=2 s 代入角速度和角加速度的表达式得
![]()
由于ε 为常量,ω、ε 同号,且为正值,故知主轴按逆时针转向匀加速转动。
(3)转动刚体上各点的速度和加速度。
因刚体绕定轴转动时,除转轴上各点外,其余所有点都在垂直于转轴的平面做圆周运动,圆心位于点所在平面与转轴的交点,半径为该点到转轴的垂直距离。因此绕固定轴线转动的刚体,其上任意一点的运动都可看作是该点在平面内的圆周运动,这个面通过该点并垂直于转轴。由于点的运动为圆周运动,故可用自然法确定点的速度和加速度。
观察转动刚体上的任意点M,该点到转轴的垂直距离为OM,通过这一点作平面与转轴垂直,这一点便在该平面内做圆周运动,其轨迹如图10-10 所示。其中圆心O 为平面与轴线的交点。
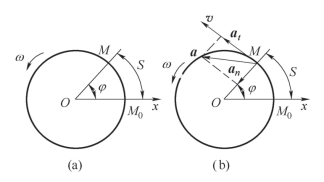
图10-10 刚体绕定轴转动
建立Ox 坐标,以轴Ox 与圆周交点MO 作为运动的起始点,并以此点作为弧坐标S 的原点。以转角φ 的增加方向作为弧坐标S 的正向。设任意瞬时刚体转过的角度为φ=φ(t),这时动点M 从M0 运动到M,M 点的弧坐标为
![]()
此即为动点的运动方程。(https://www.chuimin.cn)
考虑到圆弧的曲率半径ρ=R,则M 点的速度、切向加速度和法向加速度的大小分别为
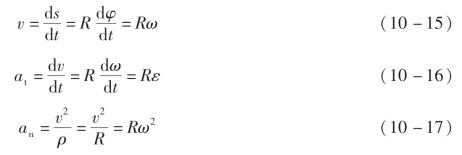
其中速度v 和切向加速度at 的方向沿圆周轨迹的切线。速度v 的指向由转向(即ω 方向)确定。因此,v 和ω 具有相同的正负号。切向加速度at 的指向与ε 和ω 的正负号有关;当ε 和ω 同号(即同向)时,at 和v 指向相同;当ε 和ω 异号(即反向)时,at 和v 指向相反。因此,at 与ε 具有相同的正负号。
根据式(10-16)和式(10-17),得到转动刚体上任意一点的加速度a 的大小及其与法线之间的夹角分别为
![]()

由于转动刚体在任意瞬时的角速度和角加速度数值都是确定的,故上述结果式(10-15)至式(10-19),可以得到如下结论:
(1)刚体绕固定轴线转动时,其上各点的速度和加速度大小均与点到转轴的垂直距离成正比。
(2)刚体上所有点在任意瞬时的加速度a 与点的圆周运动轨迹半径之间的夹角α,具有相同的数值,并且只与刚体在这一瞬时的角速度和角加速度有关,而与此点到转动中心的距离无关。
图10-11(a)、图10-11(b)所示分别为垂直转轴平面内沿半径方向各点的速度和加速度分布图。
案例10-4 半径为R=0.2 m 的转轮垂直于图示平面的O 轴逆时针方向转动,如图10-12 所示。已知:转轮的转动方程为φ=t2 +4t,其中φ 以rad 计,t 以s 计。(1)试计算t=1 s时,转轮外缘上任意点M 的速度和加速度。(2)如果在转轮外缘上饶一不可伸长的绳索,绳索另一端悬挂物体A。试计算t=1 s 时,物体A 的速度和加速度。
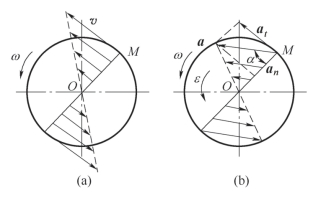
图10-11 沿半径方向各点的速度和加速度分布图
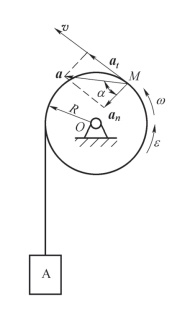
图10-12 转轮
分析:(1)计算转轮外缘上任意点的速度和加速度。根据ω=dφ/dt 和ε=dω/dt,由已知转动方程φ=t2 +4t 得到转轮外缘上任意瞬时的角速度和角加速度分别为
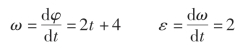
当t=1 s 时,由上式,得角速度和角加速度分别为
![]()
根据
![]()
转轮外缘上任意点的速度和加速度的大小为
![]()
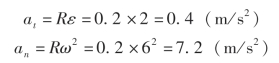
其速度v 的方向沿M 点的切线方向,指向如图10-12 所示。因为当ε 和ω 同号(即同向)时,at 和v 指向相同,at 指向圆心O。
根据a=![]() M 点的加速度a 的大小及其与法线(即半径方向)之间的夹角分别为
M 点的加速度a 的大小及其与法线(即半径方向)之间的夹角分别为
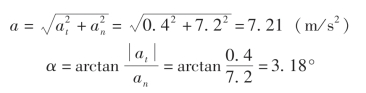
(2)计算物体A 的速度和加速度。因为以假设绳索不可伸长,所以物体下降的距离与转轮外缘上任意点在同一时间内所走过的弧长相等,于是有
![]()
根据v=ds/dt 和直线运动时a=dv/dt。对上式对时间分别求一次和二次导数,得
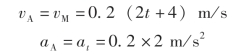
这表明,物体A 的速度和加速度分别等于转轮外缘上任意点的速度和切向加速度的数值。当t=1 s 时,有
![]()
根据转轮外缘上任意点的速度和切向加速度的方向,物体A 的速度方向向下,加速度方向也向下。
相关文章

为了降低梯级链与梯级轮啮合时的噪声,梯级轮的轮齿具有消声装置。这种张紧装置通过张紧架上的链轮直接对梯级链进行张紧,又称为滚动式张紧装置,具有张紧作用稳定的优点。张紧力来自尾部的弹簧,调节弹簧被压缩量即可调节对梯级链的张紧力。梯级链张紧装置整体工作寿命也应按不小于140000h设计。......
2025-09-29

如图3-3-1所示,主驱动轴安装在自动扶梯的上端部,轴体上安装有主驱动轮、梯级链轮、扶手带驱动链轮和附加制动器(如有)。主驱动轮一般是安装在梯级链轮上的,用高强度螺栓加以固定。其中梯级链轮必须是双侧安装,同步驱动桁架两侧的梯级链。对扶手带驱动链轮而言,根据不同的设计,有的安装在主轴体的中间位置,也有的安装在主轴的两个端部,用高强度螺栓加以固定在梯级链轮上。......
2025-09-29

工艺对象从用户程序中收到运动控制命令,在运行时执行并监视执行状态。驱动是由CPU产生脉冲对“轴”工艺对象操作先进控制的。进行参数组态前,需要添加工艺对象。添加完成后,可以在项目树中看到添加好的工艺对象,双击“组态”项进行参数组态,如图9-29所示。工艺对象报故障,在故障被确认以后,轴可以恢复在工作范围内的运动。图9-35 调试控制面板“命令”项可选择如何驱动电动机,包括点动控制、位置控制、寻找参考点等。......
2025-09-29

图3.86张角型机械手带有活塞的驱动结构总的来说,气动驱动在自动化技术中占有一席之地,并且在全球的大多数应用中使用。图3.87电机转速和机械手行程图3.88电动机械手闭合节拍内的行程和速度机械手传动机构也受到该控制的保护,否则不一定能实现机械手长时间的使用寿命。图3.91使用平直式电机安装的电动机械手的应用范例液压系统用于对夹持力要求特别高的应用,例如锻造部门。......
2025-09-29

图3-23 打击杆1/2轴截面模型1—绿色虚线 2—红色虚线结构优化后,轴销的有限元模型如图3-24所示。图3-24 结构优化后轴销的有限元模型轴销结构优化后,合分闸过程中其应力应变最大的前10个节点信息如图3-25所示,可见16242号节点在0.0272s时刻,受到的最大冲击应力为645.79MPa,材料的最大应变为0.004。图3-27 结构优化后,轴销的寿命分布云图a)A3钢 b)调质45钢 c)调质40Cr图3-28 结构优化前后的轴销寿命对比......
2025-09-29

西美尔认为时尚外在于个体,时尚向个体展现的易变性是个体自我稳定感的对照,在对照中,个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为,作为一种大众行为,时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中,西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29

图3.78不同力传导的三维说明对于应用中机械手最佳选择的问题并不容易回答。然而,当看到张角型机械手的夹持力变化过程与平动型机械手相比时,夹持力变化过程对于决策的相对重要性变得清晰。张角型机械手将根据手指的位置呈现不同的夹持力。相比之下,平动型机械手在整个手指行程中提供恒定的夹持力。......
2025-09-29
相关推荐