液压传动的主要优点有:①液压传动可以在很大的调速范围内较方便地实现无级调速。液压传动的主要缺点有:①液压传动存在不可避免的液体泄漏,同时液体不是绝对不可压缩的,故不能保证严格的传动比。总的说来,液压传动优点是主要的,而其缺点将会随着科学技术的发展、设计制造水平的提高而逐步得到解决,液压传动将会得到更广泛的应用。......
2023-06-18
点的运动方程的分析介绍，
【摘要】：x、y 均为时间t 的单值连续函数，即式称为点的直角坐标表示的运动方程。将不同瞬时的t 值代入直角坐标表示的点的运动方程，求出相应的坐标值，即确定了各瞬时点在空间的位置，将它们连接成光滑曲线，即可得到动点的运动轨迹。此外，还可以消去式中的参变量t，得到两坐标间的函数关系这样，也可得到动点的轨迹方程。试求当OA 杆按φ=kt 的规律转动时，点m 的运动方程和轨迹方程。列直角坐标表示的M 点的运动方程。求点M 的轨迹方程。
设动点M 相对于参考系Oxy 运动，则M 点在任一瞬时t 的位置可由其坐标x、y 来确定（图10-2）。x、y 均为时间t 的单值连续函数，即
式（10-1）称为点的直角坐标表示的运动方程。由这个方程可以求出任一瞬时动点的坐标x、y，从而确定了该瞬时点在空间的位置。
将不同瞬时的t 值代入直角坐标表示的点的运动方程，求出相应的坐标值，即确定了各瞬时点在空间的位置，将它们连接成光滑曲线，即可得到动点的运动轨迹。此外，还可以消去式（10-1）中的参变量t，得到两坐标间的函数关系
这样，也可得到动点的轨迹方程。
图10-2 点的运动
案例10-1 绘图仪如图10-3 所示，当杆OA 绕O 点转动时，点M 即画出一条曲线。已知OA=AB=l，CM=DM=AC=AD=a。试求当OA 杆按φ=kt 的规律转动时（式中，k 为常数，φ 以弧度计），点m 的运动方程和轨迹方程。
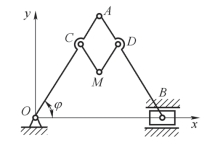
图10-3 绘图仪
分析：（1）运动分析。因M 点的轨迹尚待确定，所以必须用直角坐标法。在运动平面内建立直角坐标系Oxy（图10-3）。
（2）列直角坐标表示的M 点的运动方程。
（3）求点M 的轨迹方程。式（a）、式（b）可改写为
将式（c）、式（d）平方后相加，即得
由上式可知，点M 的轨迹为一个椭圆。
有关工程力学（第2版）的文章
- 详细阅读
-
了解钢的分类和特点的分析介绍详细阅读
钢除常用的按化学成分和用途分类外，还有一些多年来常用分类，介绍如下：1.按碳的质量分数分低碳钢 碳的质量分数低于0.25％。图4-5 金属材料按用途分类4.按冶炼方法分转炉钢 用转炉吹炼出来的钢。它按炉衬材料分为酸性平炉钢和碱性平炉钢，以碱性平炉钢为主。钢锭上部没有缩孔，只是内部有许多分散的小气泡，但钢锭外壳仍是坚实的，这些分散小气泡在轧制钢材过程中可以被压合消除掉。......
2023-06-26
-
专利权及其特点的分析介绍详细阅读
专利权，是指由专利在一定期限内依法产生的专有权利；或者说，是公民、法人或者其他组织对其发明创造在一定期限内依法享有的垄断权。在某些特殊情况下，专利权可简称为“专利”。但是，同样的发明创造在不同的法域可以分别被批准为专利。另一方面，除法律另有规定外，任何人未经专利权人许可，不得为生产经营目的实施其专利。......
2023-07-03
-
镍基合金的熔炼特点的分析介绍详细阅读
因此，熔炼镍及其合金时需要采取一定的技术措施：如采用真空熔炼法和电渣重熔法熔炼，用镁砂做炉衬。双联工艺联合熔炼是目前镍基合金的主要生产方式。其中，一次熔炼的主要目的是获得所要求的化学成分，二次重熔是为了进一步降低合金中的气体、夹杂物含量。......
2023-06-22
-
补焊修复操作要点的分析介绍详细阅读
打底层和过渡层最好采用焊条电弧焊方法操作，而且第一层要采用小直径焊条，焊后进行MT检测。对于裂纹或线性缺陷经打磨或加工消除后的坡口深度小于20mm时，采用氩弧焊补焊。焊至坡口表面时，采用坡口边缘堆焊一层或两层等措施，如图7-3和图7-4所示，深度超过20mm的坡口，先对坡口进行预包边堆焊，然后在整个坡口焊1～2层过渡层后，再采用CO2气体保护焊或焊条电弧焊填充坡口。......
2023-06-28
-
机构运动分析及运动学方程求解详细阅读
10-1 如图10-19 所示机构中，椭圆规尺长AB=40 cm，曲柄长OC=20 cm，且AC=CB。如曲柄以匀角速度ω=πrad/s 绕O 轴转动，且已知AM=10 cm，求尺上M 点的运动方程和轨迹方程；t=0 和t=0.5 s 时的M 点的速度和加速度。图10-19题10-1图图10-20题10-2图10-3 如图10-21 所示，列车沿半径为R=800 m 的圆弧轨道做匀加速运动。图10-21题10-3图10-4 荡木用两条等长的钢索平行吊起，如图10-22 所示。......
2023-06-19
-
变频器使用要点的分析介绍详细阅读
2）环境温度对变频器的使用寿命有很大的影响，环境温度每上升10℃，变频器寿命就会减半，所以变频器周围环境温度及散热的问题一定要解决好。4）变频调速系统的运行和停止，不能使用断路器和接触器直接操作，而要用变频器控制端子或变频器面板键盘来操作，否则会造成变频器失控，并可能造成变频器损坏。9）严禁用绝缘电阻表（兆欧表）等高阻表直接测量变频器的绝缘电阻。......
2023-06-19
-
深入探讨点的合成运动概念详细阅读
显而易见，在不同的参考物体上所观察的物体运动是不相同的。显然，牵连运动的类型与刚体运动类型一致。点或刚体的绝对运动是它们相对于动坐标系的相对运动与动坐标系相对于静坐标系的牵连运动的合成结果。研究运动的分析和合成问题，首先要选择好合适的静坐标系和动坐标系，然后分清什么是绝对运动、相对运动和牵连运动；最后分析各种运动的速度和加速度。......
2023-06-19
相关推荐