为了保证拉（压）杆正常工作，必须使杆内的最大工作应力σmax不超过材料的许用应力[σ]，即上式称为拉（压）杆的强度条件。利用上述强度条件，可以解决下列三种强度计算问题：1.校核强度当已知拉压杆的截面尺寸、所受外力和材料的许用应力时，通过比较工作应力与许用应力的大小，以判断该杆在所受外力作用下能否安全工作。......
2025-09-29
安全系数法应用于压杆稳定性校核
【摘要】：已知稳定安全系数nw=3，试校核压杆的稳定性。现用欧拉公式计算该杆的临界力由此可得安全工作系数为故该压杆满足稳定要求。已知连杆用硬铝制成，其外径D=38 mm，内径d=34 mm，杆长l=600 mm，规定稳定安全系数[nw]=2.5，试校核该杆的稳定性。
为了保证压杆有足够的稳定性，应使其工作压力小于临界力，或使其工作应力小于临界应力，即F ＜Fcr或σ ＜σcr，用安全系数来校核压杆稳定性，其稳定性条件为
式中 nw——压杆实际稳定安全系数；
[nw] ——规定的稳定安全系数。
案例9-5 新195 型柴油机的压杆长度l=257 mm，直径d=8 mm，弹性模量E=210 GPa，作用于压杆的最大轴向压力为1.76 kN。已知稳定安全系数nw=3，试校核压杆的稳定性。
分析：截面惯性矩为
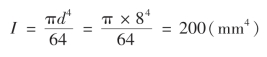
截面惯性半径为
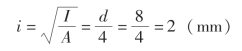
按两端铰支考虑，取μ=1，由此得压杆柔度为
可见该压杆为细长杆。现用欧拉公式计算该杆的临界力
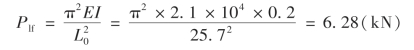(https://www.chuimin.cn)
由此可得安全工作系数为
故该压杆满足稳定要求。
案例9-6 如图9-7 所示空心圆截面连杆，承受轴向压力P=20 kW。已知连杆用硬铝制成，其外径D=38 mm，内径d=34 mm，杆长l=600 mm，规定稳定安全系数[nw]=2.5，试校核该杆的稳定性。
图9-7 空心圆截面连杆
分析：（1）计算压杆柔度。
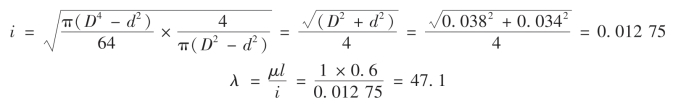
由表9-2 查得λP=50，则λ=47.1 ＜λP50，又查得a=372 MPa，b=214 MPa。
由式（9-6），得
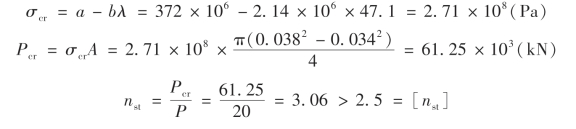
此连杆稳定性符合要求。
相关文章
- 详细阅读
-
拉（压）杆强度的计算方法详细阅读
分析：根据式（4-7）知，材料的许用应力为由强度条件式，得由于直杆横截面为圆形，所以得所以圆截面杆的直径至少为18 mm。图4-30简易悬臂吊车分析：求两杆的轴力。根据轴向拉（压）杆的强度条件，AB、BC 杆的最大应力为可见BC 杆的最大工作应力超过了材料的许用应力，所以此结构不安全。根据钢杆AB 的强度要求，有根据木杆BC 的强度要求，有可见，吊车的最大起吊量即许用载荷为FG，其值为40.4 kN。......
2025-09-29
-
欧拉公式：细长压杆临界力计算方法详细阅读
下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。......
2025-09-29
-
轴向拉压对杆的变形：胡克定律简析详细阅读
反之，在轴向压力作用下，将引起轴向的缩短和横向的增大。因此，必须研究杆件的变形。与上述两种绝对变形相对应的纵向线应变为横向线应变线应变表示的是杆件的相对变形。即式（4-5）称为虎克定律。常数E 称为材料的弹性模量，其值随材料而异，可由试验测定。试求整个杆的变形量。......
2025-09-29
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2025-09-29
-
内力与截面法：探究杆件强度和刚度的密切关系详细阅读
内力随外力的增大、变形的增大而增大，当内力达到某一限度时，就会引起构件的破坏。内力与杆件的强度、刚度等有着密切的关系。背离截面的轴力称为拉力，指向截面的轴力称为压力。这种假想用一截面将物体截开为两部分，取其中一部分为研究对象，利用平衡条件求解截面内力的方法称为截面法。可见，外力使物体产生内力和变形，不但与外力的大小有关，而且与外力的作用位置及作用方式有关。试求杆内的轴力并作出轴力图。......
2025-09-29
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2025-09-29
-
杆端位移对杆端力的影响详细阅读
已知A端的转角位移为φA，B端的转角位移为φB，A、B两端在垂直于杆轴方向上的相对线位移为ΔAB。现求由其引起的杆端内力。关于它们的正负号规定如下：杆端转角φA、φB均以顺时针方向为正；杆件两端的相对线位移ΔAB则以使整个杆件顺时针方向转动为正。再以弯矩符号MAB代替X1，用MBA代替X2，上式便可写成这就是由杆端位移φA、φB和ΔAB所引起的杆端弯矩的计算公式。此外，由静力平衡条件还可求出杆端剪力。......
2025-09-29
相关推荐