了解梁的变形过程

2025-09-29 理论教育版权反馈

【摘要】：梁受外力作用后，轴线由直线变成一条连续光滑的曲线，称为挠曲线。图7-34悬臂梁梁任一横截面的形心沿y 轴方向的线位移，称为该截面的挠度，用y 表示。增大梁的抗弯刚度。增大抗弯刚度，可以减小最大挠度，从而提高梁的刚度。在允许的情况下，适当地调整梁的载荷作用方式，可以降低弯矩，从而减小梁的变形。

1.梁弯曲变形的概念

在工程实际中，某些机器或机构中的构件，在满足强度条件的同时，还需要满足一定的刚度条件。如桥式起重机大梁AB [图7-33（a）]，过大变形使吊车产生爬坡现象，引起振动，不能平稳地吊起重物；木地板由于过大变形，引起地板下塌[图7-33（b）]；机床主轴，如果刚度不够，将严重影响加工工件的精度，传动轴的变形过大，则不仅会影响齿轮的啮合，而且会导致支承齿轮的轴颈和轴承产生不均匀磨损，既影响轴的旋转精度，又大大降低齿轮、轴及轴承的工作寿命。

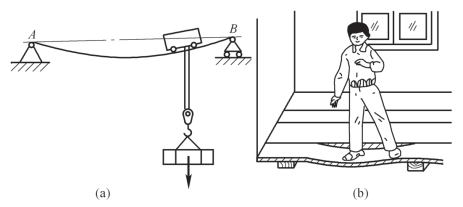
pagenumber_ebook=142,pagenumber_book=133

图7-33　弯曲变形实例

因此，对某些构件而言，刚度条件将直接影响到机器或机构的工作精度。如图7-34 所示为一悬臂梁，取直角坐标系xAy，x 轴向右为正，y 轴向上为正，平面与梁的纵向对称平面是同一平面。梁受外力作用后，轴线由直线变成一条连续光滑的曲线，称为挠曲线。梁各点的水平位移略去不计，梁的变形可用下述两个位移来描述。

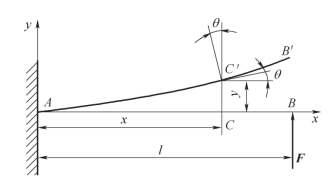
pagenumber_ebook=143,pagenumber_book=134

图7-34　悬臂梁

（1）梁任一横截面的形心沿y 轴方向的线位移，称为该截面的挠度，用y 表示。y 以向上为正，其单位是m 或mm。

（2）梁任一横截面相对于原来位置所转过的角度，称为该截面的转角，用θ 表示。θ 以顺时针为正，其单位是rad。

梁在变形过程中，各横截面的挠度和转角都随截面位置x 而变化，所以挠度y 和转角θ可表示为x 的连续函数，即

上述两式分别称为挠曲线方程和转角方程。由图7-34 可知，在小变形的情况下，梁内任一截面的转角θ 等于挠曲线在该截面处的切线的斜率，即

(https://www.chuimin.cn)

因此，只要知道梁的挠曲线方程y=y（x），就可以求得梁任意截面的挠度y 和转角θ。

2.梁的刚度条件

工程中在刚度方面对挠度和转角一般都有要求，刚度条件为

pagenumber_ebook=143,pagenumber_book=134

上述两式中的[y] 和[θ] 分别称为许用挠度和许用转角，均根据不同零件或构件对工艺的要求而确定。

3.提高刚度的途径

要提高梁的刚度，应从影响梁刚度的各个因素来考虑。梁的挠度和转角与作用在梁上的载荷、梁的跨度、支座条件及梁的抗弯刚度有关。因此要降低挠度，提高刚度，可采用以下措施。

（1）增大梁的抗弯刚度。增大抗弯刚度，可以减小最大挠度，从而提高梁的刚度。另外，增大截面的惯性矩，可以提高梁的刚度，这就要选择合理的截面形状。

（2）减少梁的跨度或改变梁的支座条件。梁的跨度对梁的挠度影响较大，要降低挠度，就要设法减小梁的长度，当长度无法减小时，则可增加中间支座，如图7-35 所示，在车床上加工较长的工件时，为了减小切削力引起的挠度，以提高加工精度，可在卡盘与尾架之间增加一个中间支架。

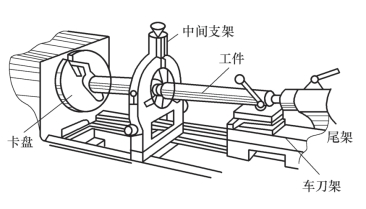
pagenumber_ebook=144,pagenumber_book=135

图7-35　增加中间支架以提高机床加工工件的刚度

（3）改善载荷的分布情况。在允许的情况下，适当地调整梁的载荷作用方式，可以降低弯矩，从而减小梁的变形。

利用积分法，列出梁的挠度方程，即可求出梁的最大挠度，承受不同载荷的梁的挠度方程可查阅相关的工程计算手册。如图7-29（a）所示承受均布载荷的简支梁，最大挠度为y=5ql4/384EIz，若将两端支承各向内侧移动2l/9 [图7-29（c）]，因缩短了梁的跨度，使梁的变形大大减小，最大挠度降为y=0.11ql4/384EIz。若增加中间支承[图7-29（e）]，则最大挠度减至原来的1/40。也就是说，仅仅改变一下支承的位置或增加支承，可将梁的刚度成倍提高。

了解梁的变形过程

相关推荐