产生最大正应力的截面称为危险截面。为了保证梁具有足够的强度，必须使梁危险截面上的最大正应力不超过材料的许用应力，即式为梁的正应力强度条件。在已知梁的横截面形状和尺寸、材料及所受荷载的情况下，可校核梁是否满足正应力强度条件。当已知梁的荷载和所用的材料时，可根据强度条件，先计算出所需的最小抗弯截面系数：然后根据梁的截面形状，再由Wz值确定截面的具体尺寸或型钢号。......
2023-06-16
梁的弯曲强度条件优化
【摘要】：图7-26简支矩形木梁分析：画出梁的弯矩图。根据弯矩图可以看出根据弯曲正应力的强度条件。由图7-27可知，梁中点截面为危险截面，其最大弯矩为由梁的弯曲强度条件经查附录，可选用28b，其Wx=534 cm3。验算梁的强度按有关设计规范，最大工作应力若不超过其许用应力的5%是允许的。已知灰铸铁的Iz=7.56 ×106 mm4，抗拉许用应力[σ] +=39.3 MPa，抗压许用应力[σ] -=58.8 MPa，试校核该梁的强度。根据式故T 形梁强度不足。
与拉伸、压缩杆的强度设计相似，工程设计中，为了保证梁足够安全，梁的危险截面上的最大正应力必须小于许用应力。
（1）当材料的拉、压强度相等，即[σ] +=[σ] -=[σ]，等直梁的弯曲强度条件为
（2）当材料的拉、压强度不相等，即[σ] +≠[σ] -，则梁的弯曲强度条件为
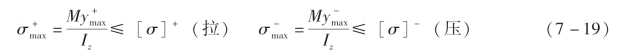
案例7-7 如图7-26 所示的简支矩形木梁AB。已知：跨度l=5 m，承受均布载荷q=3.6 kN/m，木材顺纹许用应力[σ]=10 MPa。设梁横截面高度之比为h/b=2，试选择梁的截面尺寸。
图7-26 简支矩形木梁
分析：（1）画出梁的弯矩图。
根据弯矩图可以看出
（2）根据弯曲正应力的强度条件。
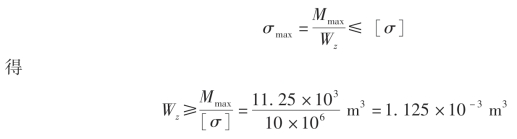
横截面为矩形，所以
整理得
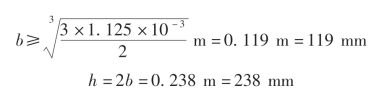
因此，可选取h×b=240 mm×120 mm 的矩形截面。
案例7-8 图7-27（a）所示的桥式起重机大梁由工字钢制成，跨长L=10 m，材料的许用应力为[σ]=160 MPa，电动葫芦重G=0.5 kN，最大起吊重量为F=32 kN。试选择工字钢的型号。
分析：（1）选择工字钢的型号。
图7-27 桥式起重机大梁
首先不考虑大梁的自重，起重机大梁的力学模型为如图7-27（b）所示的简支梁。电动葫芦移动到梁跨长的中点，梁中点截面处将产生最大弯矩，图7-27（c）为桥式起重机大梁在电动葫芦G 和最大起吊重量G 作用下的弯矩图。由图7-27（c）可知，梁中点截面为危险截面，其最大弯矩为
由梁的弯曲强度条件
经查附录，可选用28b，其Wx=534 cm3。
（2）选用工字钢后，还要验算大梁自重的影响。梁的自重可以看作是作用于梁上的均布载荷q，经查附录表1 得28b 工字钢的理论重量为其47.888 kg/m，故均布载荷为q=469 N/m。当（F+G）和q 共同作用时[图7-27（d）]，梁的弯矩图可利用叠加原理来分析。如图7-27（e）所示，梁在两种载荷共同作用下的弯矩等于每种载荷单独作用时的弯矩之和。（F+G）和q 单独作用时最大弯矩均出现在中点，因此叠加后最大弯矩仍出现在中点。
验算梁的强度
按有关设计规范，最大工作应力若不超过其许用应力的5%是允许的。故28b 工字钢的强度足够。
案例7-9 由灰铸铁制造的T 形截面外伸梁，受力及截面尺寸如图7-28 所示，其中z轴为中性轴。已知灰铸铁的Iz=7.56 ×106 mm4，抗拉许用应力[σ] +=39.3 MPa，抗压许用应力[σ] -=58.8 MPa，试校核该梁的强度。
分析：因为梁的截面没有水平对称轴，所以其截面上的最大拉应力和最大压应力不相等。同时梁的材料为灰铸铁，其抗拉许用应力与抗压许用应力亦不相等。因此判断危险截面时，应综合考虑以上因素。
（1）求解外伸梁的支座反力。列解平衡方程
∑MA（F）=0，FB ×2 000 mm-12 kN ×1 000 mm-4.5 kN ×3 000 mm=0
得
FB=12.75 kN
∑Fy=0，FA-12 kN+FB-4.5 kN=0
得
FA=3.75 kN，
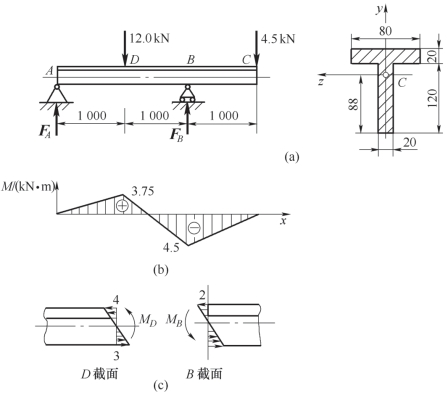
图7-28 T 形截面外伸梁
（2）作弯矩图。弯矩图如图7-28（b）所示，其中B、D 两个截面上的弯矩方向不同，如图7-28（c）所示。截面D 为正弯矩最大，截面B 为负弯矩最大。截面B 上弯矩绝对值最大，为可能的危险截面之一。
截面B 弯矩为负，其绝对值为
截面D 弯矩为正，其值为
（3）计算最大拉、压应力。B、D 截面的应力分布见图7-28（c），由于截面B 上的弯矩比截面D 上的弯矩大，所以截面B 上的压应力数值一定比截面D 上的压应力数值大。拉应力两个截面都较大，因为截面B 的弯矩M 虽大，但最大拉应力点的y 值却较小，所以截面D 也可能为危险截面，两个截面上的最大拉应力都要计算，最后比较出最大值。
截面B 最大拉应力和最大压应力作用点到中性轴的距离为
截面D 最大拉应力和最大压应力作用点到中性轴的距离为
对于截面B：最大拉应力为
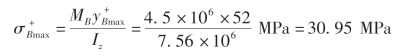
最大压应力为
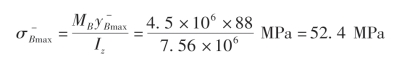
对于截面D：最大拉应力为
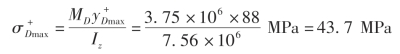
最大压应力为
经分析比较可知，整个梁上最大压应力发生在B 截面
=52.4 MPa，最大拉应力发生D 截面
=43.7 MPa
（4）强度校核。根据式（7-15）
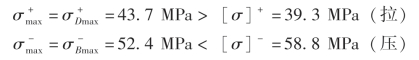
故T 形梁强度不足。
有关工程力学（第2版）的文章
- 详细阅读
-
梁的强度条件在实际工程中的应用详细阅读
在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。通常先按正应力强度条件设计出截面尺寸，然后按剪应力强度条件进行校核。但在以下几种情况下，需校核梁的剪应力：①最大弯矩很小而最大剪力很大的梁；②焊接或铆接的组合截面梁；③木梁，因为木材在顺纹方向的剪切强度较低，所以木梁有可能沿中性层发生剪切破坏。按强度条件求许用荷载[F]。......
2023-06-16
-
圆轴扭转强度的条件优化详细阅读
为了保证圆轴在扭转变形中不会因强度不足而发生破坏，应使圆轴横截面上的最大切应力不超过材料的许用切应力，即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴，直径分别为d1=40 mm，d2=55 mm，已知C 轮输入转矩MC=1 432.5 N·m，A 轮输出转矩MA=620.8 N·m，轴的转速n=200 r/min，轴材料的许用切应力[τ]=60 MPa，试校核该轴的强度。......
2023-06-19
-
纤维混凝土的压缩和弯曲强度优化技巧详细阅读
纤维混凝土的压缩强度与素混凝土相当，但能在一定程度上提高弯曲强度，提高的程度与掺量有关。体积含量达到0.5%～1%的聚丙烯纤维混凝土弯曲强度是素混凝土的1.6～1.9倍；而含量为1%和2%的高模量聚乙烯纤维混凝土抗弯强度则是素混凝土的1.8～2.3倍。另有试验得出，掺量为0.025%～0.1%的高模量聚乙烯纤维混凝土，可提高弯曲强度13%～22%；掺量0.1%的聚丙烯纤维对弯曲强度的提高仅为6%。因此有人认为，聚丙烯纤维网混凝土可作为高层建筑防火混凝土。......
2023-06-22
-
圆轴扭转的强度条件优化探讨详细阅读
圆轴扭转时横截面上的最大工作切应力τmax不得超过材料的许用切应力[τ]，即式称为圆轴扭转时的强度条件。对于等截面圆轴，从轴的受力情况或由扭矩图可以确定最大扭矩Tmax，最大切应力τmax发生于Tmax所在截面的边缘上。因而强度条件可改写为对于变截面杆，如阶梯轴、圆锥形杆等，Wt不是常量，τmax并不一定发生在扭矩为极值Tmax的截面上，这要综合考虑扭矩T和抗扭截面系数Wt两者的变化情况来确定τmax。......
2023-06-16
-
如何提高梁弯曲强度？详细阅读
影响梁的弯曲强度的主要因素是弯曲正应力，而弯曲正应力的强度条件为所以要提高梁的弯曲强度，应从如何降低梁内最大弯矩Mmax的数值及提高抗弯截面系数Wz 的数值着手。为提高梁的弯曲强度，可采取以下措施。图7-29均布载荷集中载荷作用的简支梁合理配置载荷。大的截面形状梁的合理截面应该是用较小的截面面积获得较大的抗弯截面系数，从梁横截面正应力的分布情况来看，应该尽可能将材料放在离中性轴较远的地方。......
2023-06-19
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2023-06-16
- 详细阅读
相关推荐