实际上，在载荷集度、剪力和弯矩之间存在着普遍的微分关系。由此表明弯矩图的变化形式与载荷集度q的正负值有关。表6-1梁上荷载和剪力图、弯矩图的关系利用梁的剪力图、弯矩图与荷载之间的规律作梁的内力图，通常称为简捷法作剪力图、弯矩图。梁的端截面、集中力、集中力偶的作用截面、分布荷载的起止截面都是梁分段时的界线截面。......
2023-06-16
载荷集度与剪力、弯矩的微分关系及应用
【摘要】：根据上述微分关系，可以得到下述推论，这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。因此，对于受均布载荷作用的一段梁上，其剪力图为一倾斜直线，而弯矩图为抛物线。在集中力作用截面的左、右两侧，剪力FQ 有一突然变化，弯矩图的斜率也发生突然变化，成为一个折点。表7-1梁的剪力图和弯矩图的规律案例7-5 外伸梁及其所受载荷如图7-16所示，试作梁的剪力图和弯矩图。
从上面几个例题可以看出，由于载荷不同，梁的剪力图和弯矩图也就不同；在案例7-4中曾经指出，在FQ=0 的截面上，弯矩有极值等。这些都说明载荷、剪力、弯矩间存在着一定关系，下面来分析这种关系。
轴线为直线的梁[图7-15（a）]，受载荷作用，其中坐标轴的原点位于梁的左端，y轴向上为正，梁上分布载荷的集度q（x）是x 的连续函数，并规定向上为正。为了研究剪力、弯矩沿梁轴的变化情况，用横截面m-m 和n-n 从梁中截取一微段dx 来分析[图7-15（b）]，有分布载荷q（x）和两端截面上的剪力、弯矩。由于所取的dx 为微量，故可把q（x）看成是均布载荷。
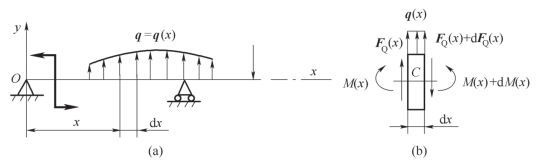
图7-15 简支梁
在这些力的作用下，微段处于平衡状态。由平衡方程∑Fy=0 和∑MC=0，得
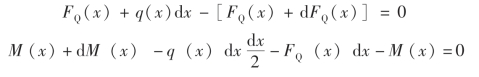
略去第二式中的高阶微量
，得
这就是直梁微段的平衡方程。由式（7-1）和式（7-2）可进一步得到
式（7-1）～式（7-3）表示了直梁的q（x）、FQ（x）和M（x）间的微分关系。
根据上述微分关系，可以得到下述推论，这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。
（1）在梁的某一段内，若无分布载荷作用，即q（x）=0，由式（7-1）可知，在该段梁上FQ（x）=常数，剪力图是平行于x 轴的直线。再由式（7-2）可得M（x）是x 的线性函数，其弯矩图为一倾斜直线。
（2）在梁的某一段内，若作用着均布载荷，即q（x）=常数，由式（7-3）可知，FQ（x）为x 的线性函数，M（x）为x 的二次函数。因此，对于受均布载荷作用的一段梁上，其剪力图为一倾斜直线，而弯矩图为抛物线。
在梁的某一段内，若分布载荷q（x）向下，这表明弯矩图应为向上凸的曲线；反之，若分布载荷向上，则弯矩图应为向下凹的曲线。
（3）若在梁的某一截面上FQ（x）=0，则在这一截面上弯矩具有一极值（极大或极小），即弯矩的极值发生于剪力为零的截面上（案例7-4）。
在集中力作用截面的左、右两侧，剪力FQ 有一突然变化，弯矩图的斜率也发生突然变化，成为一个折点。弯矩的极值就可能出现于这类截面上（案例7-2）。
在集中力偶作用截面的左、右两侧，弯矩发生突然变化（案例7-3），这也可能出现弯矩的极值。
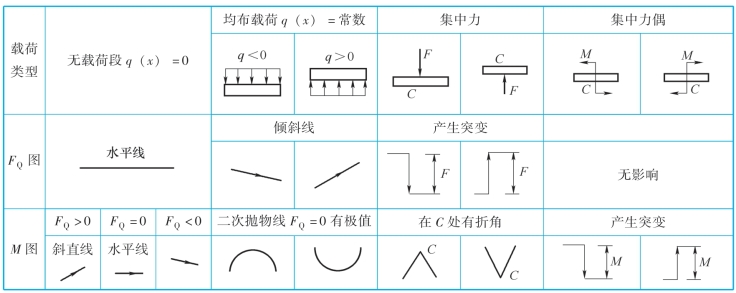
根据集中力、集中力偶作用处内力图的变化规律，可以将剪力图、弯矩图和梁上载荷三者之间的一些常见的规律小结如表7-1 所示。
表7-1 梁的剪力图和弯矩图的规律
案例7-5 外伸梁及其所受载荷如图7-16（a）所示，试作梁的剪力图和弯矩图。
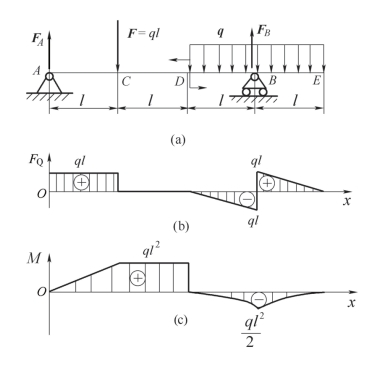
图7-16 外伸梁
分析：（1）由平衡方程求得支座反力为
（2）绘制剪力图。A 截面上有向上的支座反力FA，因此A 截面的剪力有突变，突变值为ql。AC 段梁上无载荷，剪力为常量，即FQ=ql。C 截面有向下的集中力F=ql，剪力有突变，故C 截面右侧的剪力FQ=ql-ql=0。CD 段无载荷，所以剪力为常量FQ=0。DB 段有均布载荷，剪力图为斜直线，B 截面左侧剪力FQ=-ql。B 截面有支座反力，剪力有突变，突变值为2ql，故截面右侧剪力FQ=2ql-ql=ql。BE 段有均布载荷，剪力图为斜直线，E截面剪力为零。因此可作出剪力图，如图7-16（b）所示。
（3）绘制弯矩图。A 截面上弯矩MA=0，AC 段上剪力为常量，故弯矩图为斜直线，C 截面上的弯矩M=ql2。CD 段上剪力为零，故弯矩图为与轴线平行的直线。D 截面有集中力偶作用，弯矩有突变，突变值为ql2，故D 截面右侧弯矩M=ql2-ql2=0。DB 和BE 段上有均布载荷q，弯矩图为抛物线，D 截面右侧与E 截面上的剪力FQ=0，所以D 截面和E 截面的弯矩有极值，且均为极小值零，B 截面上有支座反力，故弯矩图上有折点，大小为ql2/2。从而可作弯矩图，如图7-16（c）所示。
案例7-6 迅速绘制如图7-17 所示的简支梁的剪力图和弯矩图。
分析：（1）求支座反力，列平衡方程如下
∑MA（F）=0 FB×3-32-40×1=0 得FB=24 kN
∑Fy=0 FA+FB-40=0 得FA=16 kN
（2）剪力图的绘制。
从坐标原点开始画，A 处有集中力FA=16 kN，剪力图向上突变到16 kN。AC 段无载荷，剪力图为一平行于x 轴的直线。C 截面有向下的集中力40 kN，剪力图向下突变到-24 kN（16-40=-24），D 处有集中力偶，但不影响剪力，故CB 段为平行于x 的一条直线。支座B 处有向上的支座反力FB=24 kN，故剪力图向上突变回到零点。
（2）弯矩图的绘制。
从原点开始画起，AC 段为无载荷段，且由AC 段的FQ ＞0，故AC 段的弯矩图为一向上倾斜的直线，到C 截面，弯矩值为MC=FA ×1 m=16 kN·m。CD 段为无载荷段，且由CD 段的FQ ＜0，故CD 段的弯矩图为一向下倾斜的直线，到D 截面左侧，弯矩MD-=-8 kN·m。D 截面上有一顺时针转向的力偶，故在D 截面上弯矩图向上突变，由-8 kN·m 变为24 kN·m（-8 kN·m+32 kN·m=24 kN·m）。DB 段为无载荷段，且DB 段的FQ ＜0，故DB 段的弯矩图为一向下倾斜的直线，最后回到零点。
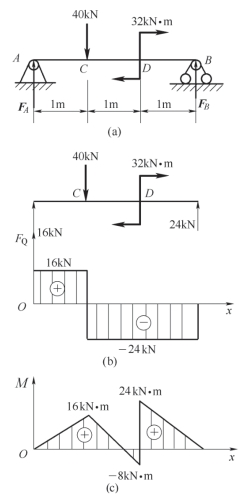
图7-17 简支梁
有关工程力学（第2版）的文章
- 详细阅读
-
剪力和弯矩的计算方法详细阅读
由上面的例子可以总结出计算梁的剪力和弯矩的具体方法：剪力FQ=截面一侧所有外力的代数和，外力的正负号规定可简记为“左上右下，剪力为正”。试求指定截面上的剪力和弯矩。弯矩的突变值等于集中力偶的力偶矩的大小。因此，应用截面法计算任意截面的弯矩时，截面不能选取在集中力偶作用的截面上。......
2023-06-19
-
边界与载荷条件的关系详细阅读
细观模型的边界条件和损伤断裂模式有比较直接的关系，本节在模型左、右两端考察了三种边界条件对计算结果的影响。在上端采用垂直位移加载控制来模拟单轴拉伸和压缩条件。在下端施加垂直方向约束。计算结果和Arora 等［16］得到的结论一致。图8－16拉伸载荷下三种边界条件的计算结果自由边界；耦合直边；周期性边界图8－17压缩载荷下三种边界条件的计算结果自由边界；耦合直边；周期性边界......
2023-06-27
-
如何绘制剪力图和弯矩图？详细阅读
以平行于梁轴的横坐标x 表示横截面的位置，以纵坐标表示相应横截面上的剪力和弯矩，绘出剪力方程和弯矩方程的图线，这样的图线分别称为剪力图和弯矩图。作剪力图和弯矩图。试列出此梁的剪力方程和弯矩方程，并绘制剪力图和弯矩图。得图7-14均布载荷作用的简支梁列剪力方程和弯矩方程。由剪力图和弯矩图可以看出，梁上有均布载荷作用处，剪力图为斜直线，弯矩图为一段抛物线，且在剪力等于零的截面具有最大弯矩值。......
2023-06-19
-
剪力图和弯矩图：梁内力变化规律的图形表达详细阅读
为了形象地表明沿梁轴线各横截面上剪力和弯矩的变化情况，通常将剪力和弯矩在全梁范围内变化的规律用图形来表示，这种图形称为剪力图和弯矩图。对于非水平梁而言，剪力图可以作在梁轴线的任一侧，并标明正、负号；弯矩图作在梁受拉的一侧。根据剪力方程和弯矩方程判断剪力图和弯矩图的形状，确定控制截面的个数及内力值，作图。在集中力偶作用处，剪力图无变化，弯矩图不连续，发生突变，突变的绝对值等于集中力偶的力偶矩数值。......
2023-06-16
-
数学第三节：全微分及应用详细阅读
【课前导读】对于一元函数来说，若Δy=AΔx+ο（Δx），A为常数，则称f（x）在x处可微，其中AΔx称为微分，记作d y=AΔx.f（x）在x处可微的充要条件是f（x）在该点可导，且d y=f′（x）Δx=f′（x）d x，那么对于二元函数来说，如何推广微分定义，对应的微分和导数是否能延续这样的关系，这都是这一节我们要解决的问题.我们已经知道，二元函数对某个自变量的偏导数表示当另一个自变量固定时......
2023-10-19
-
信息量与概率的关系及工程应用详细阅读
消息中所含的信息量大小与消息发生的概率有密切关系。显然，消息中包含的信息量与消息出现的概率的倒数成比例。一般情况下，采用bit为信息量单位。因此，信息量在工程上的定义是指传输该消息时所需的最少二进制脉冲数。若要传输四个独立等概的消息之一，则至少需2位二进制脉冲，即消息具有2bit的信息量。）时，此消息需用k个二进制脉冲传送，该消息的信息量为......
2023-06-27
-
生态数据分析与建模：灵敏度分析及应用详细阅读
灵敏度分析试图测量模型的一些参数、强制函数、状态变量初始值，或子模型对最重要状态变量的灵敏度。因此，对于参数P的灵敏度定义如下：S＝［x/x］/［P/P］式中：x代表所考虑的状态变量。通常需要在两个或多个水平上发现参数变化的灵敏度，因为参数和状态变量之间的关系很少是线性的。如果发现所观察的状态变量对某个子模型很灵敏，应该考虑哪几个别的子模型可以替换使用，这些子模型应在野外或实验室做进一步的具体检验。......
2023-11-17
相关推荐