实际上，在载荷集度、剪力和弯矩之间存在着普遍的微分关系。由此表明弯矩图的变化形式与载荷集度q的正负值有关。表6-1梁上荷载和剪力图、弯矩图的关系利用梁的剪力图、弯矩图与荷载之间的规律作梁的内力图，通常称为简捷法作剪力图、弯矩图。梁的端截面、集中力、集中力偶的作用截面、分布荷载的起止截面都是梁分段时的界线截面。......
2025-09-29
剪力和弯矩的计算方法
【摘要】：由上面的例子可以总结出计算梁的剪力和弯矩的具体方法：剪力FQ=截面一侧所有外力的代数和，外力的正负号规定可简记为“左上右下，剪力为正”。试求指定截面上的剪力和弯矩。弯矩的突变值等于集中力偶的力偶矩的大小。因此，应用截面法计算任意截面的弯矩时，截面不能选取在集中力偶作用的截面上。
根据上述规则，对水平梁的某一指定截面来说，在它左侧的向上外力，或者右侧的向下外力，将产生正的剪力；反之，将产生负的剪力。截面左侧的外力对截面形心的力矩为顺时针转向或者截面右侧的外力对截面形心的力矩为逆时针转向时，产生正的弯矩，反之则产生负的弯矩。对于弯矩，不难发现，无论在指定截面的左侧还是右侧，向上的外力产生正的弯矩，向下的外力产生负的弯矩。
由上面的例子可以总结出计算梁的剪力和弯矩的具体方法：
（1）剪力FQ=截面一侧所有外力的代数和，外力的正负号规定可简记为“左上右下，剪力为正”。
（2）弯矩M=截面一侧所有外力对截面形心力矩的代数和，力矩的正负号规定可简记为“左顺右逆，剪矩为正”。
案例7-1 如图7-11 所示的外伸梁，已知均布载荷的载荷集度为q，集中力偶的力偶矩为M=3qa2，设2-2 截面到A 截面的距离为Δ，当Δ→0，2-2 截面称为A 截面的左临近截面。同理，3-3 截面称为A 截面的右临近截面，4-4 截面称为C 截面的左临近截面，5-5截面称为C 截面的右临近截面。试求指定截面上的剪力和弯矩。
分析：（1）求梁的支座反力。选取梁的整体为研究对象，受力图如图7-11 所示。列平衡方程
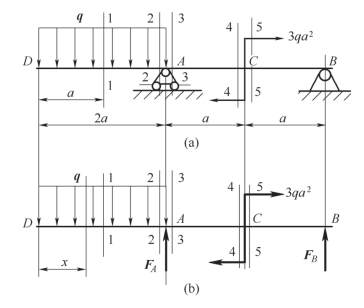
图7-11 外伸梁
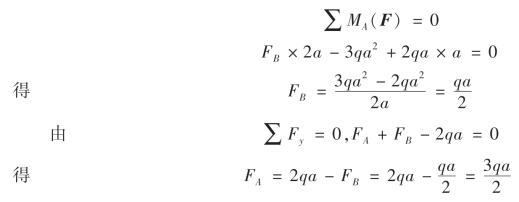
（2）计算指定截面的剪力和弯矩。
观察1-1 截面左侧上所有的外力qa 向下，在1-1 截面产生的剪力为负；qa 对1-1截面形心的力矩为逆时针转向，在1-1 截面产生的弯矩为负。由剪力和弯矩的计算法则，1-1 截面上剪力和弯矩分别为(https://www.chuimin.cn)
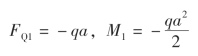
观察2-2 截面左侧所有的外力2qa 向下，在2-2 截面产生的剪力为负；2qa 对2-2截面形心的力矩为逆时针转动，在2-2 截面产生的弯矩为负。2-2 截面上的剪力和弯矩分别为
观察3-3 截面左侧上所有的外力2qa 向下，在3-3 截面产生的剪力为负；2qa 对3-3截面形心的力矩为逆时针转向，在3-3 截面产生的弯矩为负。FA 向上，在3-3 截面产生的剪力为正；FA 通过3-3 截面形心，在3-3 截面产生的弯矩为零。3-3 截面上的剪力和弯矩分别为
观察2-2 截面与3-3 截面剪力和弯矩的表达式可以看出：在集中力作用的截面处，左右临近截面的弯矩相同，剪力不同，即剪力有突变。剪力的突变值等于集中力的大小。因此，应用截面法计算任意截面的剪力时，截面不能选取在集中力作用的截面上。
观察4-4 截面右侧上所有的外力FB 向上，在4-4 截面产生的剪力为负；FB 对4-4截面形心的力矩为逆时针转动，在4-4 截面产生的弯矩为正。力偶3qa2 为顺时针转向，在4-4 截面上产的弯矩为负。4-4 截面上的剪力和弯矩分别为
观察5-5 截面右侧上所有的外力，FB 向上，在5-5 截面产生的剪力为负；FB 对5-5截面形心的力矩为逆时针转向，在4-4 截面产生的弯矩为正。5-5 截面上的剪力和弯矩分别为
观察4-4 截面与5-5 截面剪力和弯矩的表达式可以看出：在集中力偶作用的截面处，左右临近截面的剪力相同，弯矩不同，即弯矩有突变。弯矩的突变值等于集中力偶的力偶矩的大小。因此，应用截面法计算任意截面的弯矩时，截面不能选取在集中力偶作用的截面上。
相关文章
- 详细阅读
-
计算方法和步骤详解详细阅读
电流密度J的分布情况通过求解公式（6-1）来获得。在本节中，动静导电杆的材料采用铜，动静触头的材料采用银，电弧的电导率为银的10-4。在ANSYS有限元软件中进行静态传导电流分析，需要经过单元类型选择、定义材质属性、分配材质属性、几何模型剖分、定义边界条件、加载激励和结果处理这几个步骤。将上一步所得电流密度分布情况作为激励加载至模型上，通过有限元分析计算，可以得到灭弧室内的空间磁场分布。......
2025-09-29
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2025-09-29
-
射击精度：衡量射击精准度的尺度和计算方法详细阅读
射击偏差是衡量射击精度的尺度,是由诸元偏差与散布偏差引起的。射击密集度, 表示各个弹着点对散布中心偏离程度的总体度量。它通常以字母E 表示, 以长度单位计量。对不同的国家或不同的武器, 表示射弹散布或射击密集度的方法各有不同。理论分析可以证明R50 =1.75E, R100 =R50。图1-4圆形散布面上的散布圆半径射击精度都是由实际射击结合理论计算来确定的。......
2025-09-29
-
梯级链的设计、安全系数和使用寿命计算方法详细阅读
梯级链是自动扶梯最重要的驱动部件，各部件应按无限疲劳寿命进行设计，因此其安全系数最小为5。重载型扶梯一般要求采用安全系数为8的梯级链。梯级链受力计算 梯级链的受力通常需考虑乘客的载荷、梯级链的张紧力及梯级和梯级链自重等，下面介绍一种计算方法。梯级链的使用寿命主要取决于销轴比压，该计算以自动扶梯的制动载荷进行校核。......
2025-09-29
-
散热系数的计算方法和影响因素：Nul数、导热详细阅读
在自由对流条件，对流散热系数可按式计算式中 Nul——努基尔数；λ——空气的导热系数；l——空气流过表面的长度。表5-3 公式中长度c、n和长度l的选择对流散热系数α是温度的函数，它随温度而变化。在热分析时，为了与对流散热的形式一致，将辐射散热通过表面散热系数简化为公式所示。因此，外表面的散热系数为α=αcon+αrad......
2025-09-29
-
剪切的常见计算方法详细阅读
剪切试验试件的受力情况应模拟零件的实际工作情况进行。若以A 表示销钉横截面面积，则应力为τ 与剪切面相切，故为切应力。以上计算是以假设“切应力在剪切面上均匀分布”为基础的，实际上它只是剪切面内的一个“平均切应力”，所以也称为名义切应力。当F 达到Fb 时的切应力称剪切极限应力，记为τb。对于图5-8 所示的剪切试验，剪切极限应力为用τb 除以安全系数n，即得到许用切应力这样，剪切计算的强度条件可表示为......
2025-09-29
-
极惯性矩Ip和抗扭截面系数Wp的意义和计算方详细阅读
极惯性矩和抗扭截面模量都是截面图形的几何性质，可以根据定义由积分法求出。AC 段和CB 段轴横截面的极惯性矩分别为计算应力。......
2025-09-29
相关推荐