为了保证圆轴在扭转变形中不会因强度不足而发生破坏,应使圆轴横截面上的最大切应力不超过材料的许用切应力,即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴,直径分别为d1=40 mm,d2=55 mm,已知C 轮输入转矩MC=1 432.5 N·m,A 轮输出转矩MA=620.8 N·m,轴的转速n=200 r/min,轴材料的许用切应力[τ]=60 MPa,试校核该轴的强度。......
2023-06-19
1.平面假设
取一圆轴进行扭转试验,试验前在圆轴表面作出若干等距的圆周线和纵向线,如图6-12(a)所示。实验时,圆轴一端固定,另一端施加外力偶。在外力偶的作用下,圆轴发生扭转变形。在变形微小的情况下,可以观察到以下现象:
(1)各圆周线均绕轴线相对旋转过一个角度,但形状、大小及相邻两圆周线之间的距离均无变化。
(2)所有纵向线仍保持为直线,但都倾斜了一个微小角度γ,使圆轴表面的小矩形变为平行四边形。
根据观察到的现象,可以假设:圆轴的横截面变形后仍为平面,其形状和大小不变,仅绕轴线发生相对转动(无轴向移动),这一假设称为圆轴扭转时的平面假设。按照这一假设,在扭转变形中,圆轴的横截面就像刚性平面一样,一个接着一个产生绕轴线的相对转动,如图6-12(b)所示,右端面相对左端面绕轴线旋转了一个角度φ。

增加动画
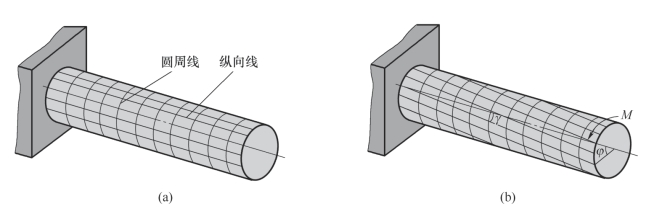
图6-12 圆轴扭转变形试验
按照平面假设,可得以下推论:
(1)横截面上无正应力。因扭转变形时,圆轴相邻横截面间距不变,即圆轴没有纵向变形发生,所以横截面上没有正应力。
(2)横截面上有切应力。因扭转变形时,相邻横截面间发生相对转动,截面上各点相对错动,发生了剪切变形,所以横截面上有切应力。
(3)切应力方向与半径垂直。因半径长度不变,故切应力方向必与半径垂直。
(4)圆心处变形为零,圆轴表面变形最大。
2.圆轴的扭转切应力分布规律
为了弄清楚横截面上各点切应变γρ 的分布规律及其与圆周表面的切应变γ 的关系,用两个垂直于轴线的平面从圆轴上截取一长为dx 的微段来研究(图6-13),则微段左右两侧面的相对扭转角为dφ,纵向线AB 倾斜小角度γ 成为AC。由几何关系可得
![]()
由此得
![]()
而在任意半径ρ 处的纵向线A′B′,根据平面假设转过dφ 后成为A′C′,其相应倾角为γρ,如图6-13 所示。由于是小变形,由图6-13 可知:B′C′=γρdx=ρdφ。于是
![]()
由于任意指定截面上,![]() 为常量,故由式(6-3)可知:横截面上任一点的切应变γρ 与该点到轴心的距离成正比,有ρ=0,γρ=0;ρ=R,γρ=γmax=γ。
为常量,故由式(6-3)可知:横截面上任一点的切应变γρ 与该点到轴心的距离成正比,有ρ=0,γρ=0;ρ=R,γρ=γmax=γ。
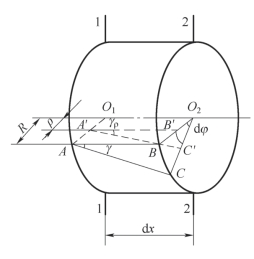
图6-13 横截面上切应变
切应力与切应变之间存在一定物理关系,由剪切胡克定律可知:当切应力不超过某一极限值时,切应力与切应变成正比,即τ=G·γ
由此,可得到圆轴扭转时横截面上各点的切应力为
![]()
上式表达了切应力在横截面上的分布规律:由于任意指定截面上,![]() 为常量,横截面上任意点处的切应力τρ 与该点到圆心的距离ρ 成正比,即τρ 沿半径呈线性变化。当ρ=0时,τρ=0;当ρ=0 时,τρ=τmax。又因为切应变γρ 发生在垂直于半径的平面内,所以横截面上各点切应力的方向垂直于半径且与扭矩的方向一致。实心圆轴与空心圆轴横截面上切应力分布如图6-14 所示。
为常量,横截面上任意点处的切应力τρ 与该点到圆心的距离ρ 成正比,即τρ 沿半径呈线性变化。当ρ=0时,τρ=0;当ρ=0 时,τρ=τmax。又因为切应变γρ 发生在垂直于半径的平面内,所以横截面上各点切应力的方向垂直于半径且与扭矩的方向一致。实心圆轴与空心圆轴横截面上切应力分布如图6-14 所示。

图6-14 切应力分布图
(a)实心圆轴;(b)空心圆轴
3.横截面上任意点的切应力大小
为了计算切应力数值,必须从静力学方面来考虑,建立切应力与扭矩T 之间的关系。如图6-15 所示:微面积dA 上内力τρdA 对O 点的矩为dM=ρτρdA,整个截面上微内力矩的合力矩应该等于扭矩T,即
![]()
式(6-5)表明了切应力与扭矩的关系。
将式(6-4)中的τρ 值代入式(6-5),得
![]()
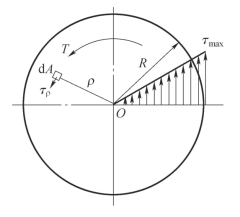
图6-15 横截面应力分布
此处dφ/dx 为单位长度上的相对扭角,对同一横截面,它应为不变量。
式(6-6)中的积分![]() 只取决于横截面的大小和形状,称为横截面对形心的极惯性矩,单位为m4,以Ip 表示,即
只取决于横截面的大小和形状,称为横截面对形心的极惯性矩,单位为m4,以Ip 表示,即
![]()
则式(6-6)可写为

将上式代回式(6-4),即得横截面上距圆心为ρ 处的切应力计算公式为
![]()
对于确定的轴,Ip 都是定值。则在圆截面边缘上,当ρ 为最大值R 时,得最大剪应力为
![]()
令 则上式变为
则上式变为

式中 Wp——抗扭截面模量,单位为m3 或cm3。
应当注意:
(1)应力计算公式只适用于弹性范围内圆截面轴扭转,且τmax不超过材料的比例极限的情况。
(2)扭转切应力的分布不同于一般剪切应力,前者组成一个力偶,后者则组成一个力。两种情况下的切应力计算公式完全不同。
有关工程力学(第2版)的文章

为了保证圆轴在扭转变形中不会因强度不足而发生破坏,应使圆轴横截面上的最大切应力不超过材料的许用切应力,即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴,直径分别为d1=40 mm,d2=55 mm,已知C 轮输入转矩MC=1 432.5 N·m,A 轮输出转矩MA=620.8 N·m,轴的转速n=200 r/min,轴材料的许用切应力[τ]=60 MPa,试校核该轴的强度。......
2023-06-19

下面以图6-8所示两端承受外力偶矩M 作用的圆轴为例,说明求任意横截面m-m 上内力的方法。用一假想截面沿m-m 将轴截开,任取一段(如左段),如图6-8所示。由于圆轴是平衡的,因此截取部分也处于平衡状态,根据力偶的性质,横截面m-m 上必有一个内力偶矩与外力偶矩m 平衡,我们把这个内力偶矩称为扭矩,用符号T 表示,单位为N·m 或kN·m。求扭矩时,在截面上均按正向画出扭矩,若所得为负,则说明扭矩转向与假设方向相反。......
2023-06-19

为解决圆轴扭转的强度问题,在求得横截面上的扭矩之后,还要进一步研究横截面上的应力。在整个横截面上,所有这些微力矩之和应等于该截面的扭矩T,因此将式代入得积分即为横截面的极惯性矩,因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中,T为横截面上的扭矩;IP为圆截面对圆心的极惯性矩;ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义,一般只计算其绝对值。......
2023-08-26

圆轴扭转时横截面上的最大工作切应力τmax不得超过材料的许用切应力[τ],即式称为圆轴扭转时的强度条件。对于等截面圆轴,从轴的受力情况或由扭矩图可以确定最大扭矩Tmax,最大切应力τmax发生于Tmax所在截面的边缘上。因而强度条件可改写为对于变截面杆,如阶梯轴、圆锥形杆等,Wt不是常量,τmax并不一定发生在扭矩为极值Tmax的截面上,这要综合考虑扭矩T和抗扭截面系数Wt两者的变化情况来确定τmax。......
2023-06-16

用φ表示单位长度扭转角,有为保证轴的刚度,通常规定单位长度扭转角的最大值不得超过许用单位长度扭转角[φ],即式称为圆轴扭转时的刚度条件。可见,刚度条件是4轴的控制因素。由于刚度是大多数机床的主要矛盾,所以用刚度作为控制因素的轴是相当普遍的。......
2023-06-16

在日常生活及工程实际中,有很多承受扭转的构件。以扭转变形为主的构件称为轴。在生产实际中圆轴用得较多,本章只研究圆轴的扭转问题。图6-2汽车转向轴图6-3丝锥钻杆图6-4钻探机钻杆汽车方向盘图6-5汽轮机带动发电机转动图6-6电动机带动传动轴转动在两外力偶作用下,轴产生扭转变形,其中杆件任意两截面间相对转动的角度称为扭转角,用φ 表示。......
2023-06-19

本章主要讨论圆轴扭转时应力和变形的分析计算方法,以及强度和刚度计算。杆间任意两截面间的相对角位移,称为扭转角。为了清楚地看出各截面上扭矩的变化情况,以便确定危险截面,通常把扭矩随截面位置的变化绘成图形,称为扭矩图。......
2023-06-26

在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。根据平衡条件可知,C截面上必存在一个内力偶矩T,与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩,用T表示。扭矩的单位与力矩相同,常用N·m或kN·m。图8-12与计算轴力的方法类似,用截面法计算扭矩时,通常假定扭矩为正。用截面法分别求出各段上的扭矩。......
2023-08-26
相关推荐