轴向拉压对杆的变形：胡克定律简析

2023-06-19 理论教育版权反馈

【摘要】：反之，在轴向压力作用下，将引起轴向的缩短和横向的增大。因此，必须研究杆件的变形。与上述两种绝对变形相对应的纵向线应变为横向线应变线应变表示的是杆件的相对变形。即式（4-5）称为虎克定律。常数E 称为材料的弹性模量，其值随材料而异，可由试验测定。试求整个杆的变形量。

直杆在轴向拉力作用下，将引起轴向尺寸的增大和横向尺寸的缩小。反之，在轴向压力作用下，将引起轴向的缩短和横向的增大。工程结构中有些拉、压杆，除强度应足够外，对变形也有限制。因此，必须研究杆件的变形。

1.拉（压）杆的变形

设杆件的原长为l，直径为d，承受轴向拉力F 后，变形为图4-15 虚线所示的形状。杆件的纵向长由l 变为l1，横向尺寸由d 变为d1。

pagenumber_ebook=76,pagenumber_book=67

图4-15　杆件变形图

则杆的纵向绝对变形为

杆的横向绝对变形为

但是绝对变形的大小不能反映杆的变形程度。如长度分别为1 m 与1 cm 的两根橡皮筋，它们的绝对变形均为1 mm，显然变形程度不同。为了消除杆件原尺寸对变形大小的影响用单位长度内杆的变形即线应变来衡量杆件的变形程度。

与上述两种绝对变形相对应的纵向线应变为

横向线应变

线应变表示的是杆件的相对变形。线应变ε、ε′的正负号分别与Δl、Δd 的正负号一致。

试验表明：当应力不超过某一限度时，横向线应变ε′与轴向线应变ε 之间存在正比关系，且符号相反。即

上式中，比例系数μ 称为材料的横向变形系数，或称泊松比。

2.虎克定律

轴向拉伸和压缩实验表明：当杆横截面上的正应力不超过某一限度时，正应力σ 与其相应的轴向线应变ε 成正比。即

式（4-5）称为虎克定律。常数E 称为材料的弹性模量，其值随材料而异，可由试验测定。E 的单位常用GPa。

若将式 pagenumber_ebook=77,pagenumber_book=68 代入式（4-5），则得虎克定律的另一种表达形式

pagenumber_ebook=77,pagenumber_book=68

式（4-6）表明，当杆横截面上的正应力不超过某一限度时，杆的轴向变形Δl 与轴力FN 及杆长l 成正比，而与材料的弹性模量E 横截面面积A 成反比。EA 越大，杆件变形越困难；EA 越小，杆件变形越容易。该指标反映了杆件抗拉伸（压缩）变形的能力，故乘积EA称为杆截面的抗拉压刚度。

同样弹性模量E 和泊松比μ 一样都是表征材料固有性能的常数，可由试验测定。表4-1中摘录了几种常用材料的E 和μ 值。

表4-1　几种常用材料的E 和μ 的约值

pagenumber_ebook=77,pagenumber_book=68

案例4-3 如图4-16（a）所示为阶梯杆，已知横截面面积AAB=ABC=500 mm2，ACD=300 mm2，弹性模量E=200 GPa。试求整个杆的变形量。

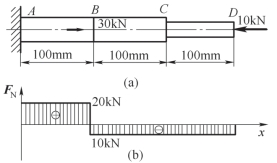
pagenumber_ebook=77,pagenumber_book=68

图4-16　阶梯杆

分析：（1）作轴力图。用截面法求得CD 段和BC 段的轴力FNCD=FNBC=-10 kN，AB段的轴力为FNAB=20 kN，画出杆的轴力图[图4-16（b）]。

（2）计算各段杆的变形量。

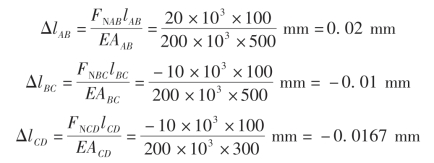
pagenumber_ebook=78,pagenumber_book=69

（3）计算杆的总变形量。杆的总变形量等于各段变形量之和，即

计算结果为负，说明杆的总变形为压缩变形。