这种变形形式称为轴向拉伸或压缩。图3-30简易吊车图3-31液压传动中的活塞图3-32拉、压杆力学简图2.杆件轴向拉伸与压缩的内力和应力内力构件工作时承受的载荷、自重和约束力，都称为构件上的外力。由于外力F 的作用线沿着杆的轴线，内力FN 的作用线也通过杆的轴线，故在轴向拉伸或压缩时，杆件的内力称为轴力。据此现象可设想，杆件......
2023-06-26
轴向拉伸与压缩引起的横截面应力分析
【摘要】：把单位面积上内力的大小称为应力，并以此作为衡量受力程度的尺度。截面上的应力可以进行分解，其中垂直于截面的应力为正应力，用字母σ 表示；平行于截面的应力称为切应力，用字母τ 表示。图4-12截面上的应力横截面正应力在国际单位制中，应力的单位是牛/米2，又称帕斯卡，简称帕。为此对杆进行拉伸或压缩实验，观察其变形。求此时斜杆AB 横截面上的正应力。
1.应力的概念
应用截面法确定了轴力后，单凭轴力并不能判断杆件的强度是否足够。例如，用同一材料制成粗细不等的两根直杆，在相同的拉力作用下，虽然两杆轴力相同，但随着拉力的增大，横截面小的杆件必然先被拉断。这说明杆件的强度不仅与轴力的大小有关，而且还与横截面面积的大小有关。为此，引入应力的概念。把单位面积上内力的大小称为应力，并以此作为衡量受力程度的尺度。截面上的应力可以进行分解，其中垂直于截面的应力为正应力，用字母σ 表示；平行于截面的应力称为切应力，用字母τ 表示。如图4-12 所示。
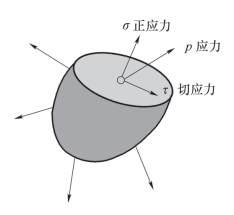
图4-12 截面上的应力
横截面正应力
在国际单位制中，应力的单位是牛/米2（N/m2），又称帕斯卡，简称帕（Pa）。在实际应用中这个单位太小，通常使用兆帕（MPa）或吉帕（GPa）。它们的换算关系为：1 N/m2=1 Pa，1 MPa=1 N/mm2=106 Pa，1 GPa=103 MPa=109 Pa。
2.拉（压）杆横截面上的应力
欲求横截面上的应力，必须研究横截面上轴力的分布规律。为此对杆进行拉伸或压缩实验，观察其变形。
取一橡胶（或其他易于变形的材料）制的等截面直杆，如图4-13（a）所示在杆上画两条与杆轴线垂直的横向线ab 和cd，然后沿杆的轴线作用拉力F，使杆件产生拉伸变形。在此期间可以观察到：横向线ab 和cd 在杆件变形过程中始终为直线，只是从起始位置分别平移到a′b′和c′d′的位置，但仍垂直于杆轴线；各纵向线伸长量相同，横向线收缩量也相同。根据这一现象，对杆内变形可作如下假设：受拉伸的杆件变形前为平面的横截面，变形后仅沿轴线产生了相对平移仍为平面，且仍与杆的轴线垂直，该假设称为平面假设。设想杆件由无数条纵向纤维所组成，根据平面假设，在任意两个横截面之间的各条纤维的伸长量相同，即变形相同。由材料的连续性、均匀性假设可以推断出内力在横截面上的分布是均匀的，即横截面上各点处的应力大小相等，其方向与横截面上轴力FN 一致，垂直于横截面，如图4-13（b）所示。
设杆件横截面的面积为A，轴力为FN，则根据上述假设可知，横截面上各点处的正应力均为：
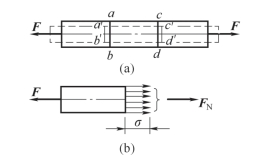
图4-13 平面假设
式中 FN——横截面轴力（N）
A——横截面面积（m2）
当轴力为正号（拉伸）时，正应力也得正号，称为拉应力；当轴力为负号（压缩）时，正应力也得负号，称为压应力。
案例4-2 如图4-14（a）所示的起重机支架，斜杆AB 为直径d=20 mm 的钢杆，载荷Q=15 kN。求此时斜杆AB 横截面上的正应力。
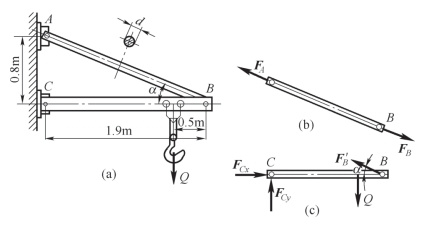
图4-14 起重机机架
分析：（1）以斜杆AB 和杆BC 为研究对象，分别画出受力图[图4-14（b）、图4-14（c）]。
（2）求斜杆AB 的内力，取BC 杆为研究对象，分析其受力图4-14（c）可列平衡方程为
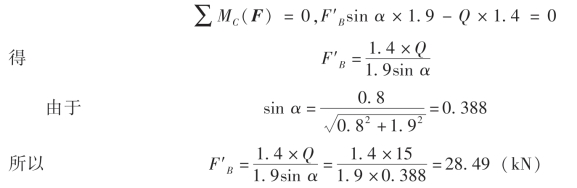
因为F′B=-FB=28.49 kN，所以斜杆AB 的内力（轴力）为FN=FB=28.49 kN。
（3）求斜杆AB 横截面上的应力，根据式（4-1）得
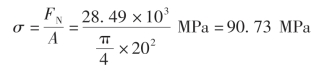
✧思考
（1）正应力的“正”指的是正负的意思，所以正应力恒大于零，这种说法对吗？为什么？
（2）两根材料与尺寸完全相同，承受外力也相同的轴向拉（压）杆，在横截面形状不同的情况下，它们的轴力图是否相同？横截面上的应力是否相同？
有关工程力学（第2版）的文章
- 详细阅读
-
轴向拉伸与压缩下的横截面内力：轴力与轴力图详细阅读
图4-9截面的内力3.轴力与轴力图轴力的概念。为保证无论取左段还是右段作研究对象所求得的同一个横截面上轴力的正负号相同，对轴力的正负号规定如下：轴力的方向与所在横截面的外法线方向一致时，轴力为正；反之为负。用截面法在AB、BC 两段，逐次计算轴力。图4-11直杆的轴力与轴力图......
2023-06-19
-
轴向拉压对横截面应力的影响详细阅读
要解决轴向拉压杆的强度问题，不但要知道杆件的内力，还必须知道内力在截面上的分布规律。下面用这种方法推导轴向拉压杆的应力计算公式。由于拉压杆的轴力是垂直于横截面的，故与它相应的分布内力也必然垂直于横截面，由此可知，轴向拉杆横截面上只有正应力，而没有剪应力。由此可得出结论：轴向拉伸时，杆件横截面上各点处只产生正应力，且大小相等[图5-9]，即式中 N——杆件横截面上的轴力；A——杆件的横截面面积。......
2023-06-16
-
轴向拉（压）杆横截面上的应力|建筑力学（第3详细阅读
由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为......
2023-08-26
-
拉伸、压缩与弯曲的组合应用技巧详细阅读
如果杆件除了在通过其轴线的纵向平面内受到垂直于轴线的荷载以外，还受到轴向拉（压）力，这时杆将发生拉伸（压缩）和弯曲组合变形。例如，如图8-3所示的烟囱，在自重作用下引起轴向压缩，在风力作用下引起弯曲，因此它是轴向压缩与弯曲的组合变形。这里首先推导（公论）扭弯组合变形的强度计算方法，计算原理和拉伸或压缩与弯曲的组合变形基本相似，本章就不作介绍。......
2023-06-16
-
纯弯曲横截面应力分布规律详细阅读
中性层与横截面的交线，称为中性轴。概括地说，纯弯曲时梁的所有横截面仍保持平面，并绕中性轴做相对转动，而纵向“纤维”则均处于单向受力状态。式（7-5）表明了梁横截面上正应力的变化规律。而要确定截面上某点的正应力的大小，还需建立应力与内力之间的静力关系。纯弯曲时梁横截面任意点的正应力计算公式，在一定条件下也适用于横力弯曲。......
2023-06-19
-
电迁移引起的背应力测量方法探析详细阅读
人们为了测定铝条带电迁移中的背应力已经付出了大量努力。电迁移测试是在260℃的温度下进行的。稳态下电阻增长速率δ/δt，和稳态下电迁移所引起的压应力梯度δσEM/δx，与电流密度的函数关系如图8.9所示。如果在铜的大马士革结构中，能够通过表面扩散机制引发电迁移，那么在结构体内，我们需要获得一个由表面扩散引发背应力的机理。......
2023-06-20
-
机械应力的分析方法详细阅读
转子所受的机械载荷即为气体爆发压力，是与热负荷共同作用，因此不单独对转子机械应力进行分析。机械载荷作用下，最大应力出现在进气道旁的螺栓孔，此处螺栓预紧力最大。因此对气缸、前端盖、后端盖机械应力分布影响较大的载荷为螺栓预紧力。而对转子而言，转子不直接受螺栓预紧力的影响，其工作过程中仅受到气体爆发压力的作用，在爆发压力的作用下运动，其应力水平较低。......
2023-06-23
相关推荐