平面任意力系是工程实际中最常见的一种力系，工程计算中的许多实际问题都可以简化为平面任意力系问题来处理。忽略摩擦和自重，当OA 在水平位置、冲压力为F 时系统处于平衡状态。由于曲轮I 承受平面任意力系作用，利用已学过的平面汇交力系平衡和力偶系平衡方程，无法求解力偶矩M 的大小。......
2023-06-19
简化平面任意力系的方法介绍
【摘要】：在平面内任取一点O，称为简化中心。图3-31平面力系的简化过程与结果简化方法：应用力的平移定理，把各力都平移到点O。因为力偶对于平面内任意点的矩都相同，因此当力系合成为一个力偶时，主矩与简化中心的选择无关。
1.主矢、主矩
刚体上作用有一平面任意力系F1、F2、…、Fn，如图3-31（a）所示。在平面内任取一点O，称为简化中心。
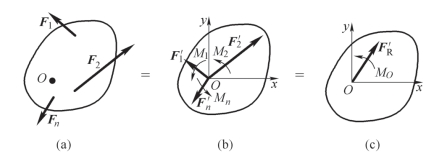
图3-31 平面力系的简化过程与结果
简化方法：应用力的平移定理，把各力都平移到点O。这样，得到作用于点O 的平面汇交力系
和一个附加平面力偶系M1，M2，…，Mn，如图3-31（b）所示。且有
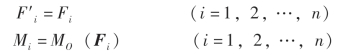
（1）平面汇交力系F1，F2，…，Fn可以合成为一个作用在O 点的力FR，如图3-31（c）所示，即力FR等于原来各力的矢量和，将这个力FR称为原力系的主矢。
将上式写成直角坐标系下的投影形式为
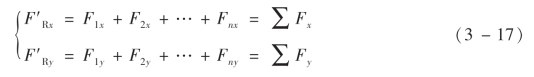
因此主矢的大小及其与x 轴正向的夹角α 分别为
（2）平面力偶系M1，M2，…，Mn 可合成为一个力偶，这个力偶的矩MO 等于各附加力偶矩的代数和，即这个力偶的矩等于原来各一个力对简化中心O 点的矩的代数和，将MO 称为原力系对简化中心的主矩。
由上面的结果，可以得出这样的结论：一般情况下，平面一般力系向作用面内任选一点O 进行简化，可得一个力和一个力偶，这个力等于该力系的主矢，作用线通过简化中心O，这个力偶的矩等于该力系对于O 点的主矩。
由于主矢等于各力的矢量和，所以它和简化中心的选择无关。而主矩等于各力对于简化中心的矩的代数和，当取不同的点作简化中心时，各力的力臂将有改变，各力对简化中心的矩也会改变，一般情况下主矩与简化中心的选择有关。所以，以后说到主矩时，必须指出是力系对哪一点的主矩。
2.固定端约束的简化
现在利用力系向一点简化的方法，分析固定端支座的约束反力。
固定端支座对物体在接触面上作用了一群约束反力。在平面问题中，这些力为一平面任意力系，如图3-32（a）所示。将这群力向作用平面内点A 简化，得到一个力和一个力偶，如图3-32（b）所示。一般情况下这个力的大小和方向均为未知量，可用两个正交分力来代替。因此，在平面力系情况下，固定端A 处的约束作用力可简化为两个约束力FAx、FAy和一个约束力偶MA，如图3-32（c）所示。
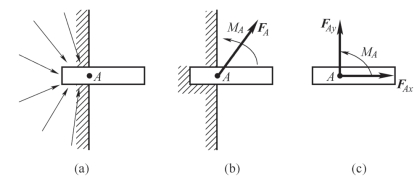
图3-32 固定端约束的简化
3.平面任意力系的简化结果
平面任意力系向作用面内一点简化的结果，通常为一个主矢FR和一个主矩MO，进一步分析有以下四种情况：
（1）F′R=0，MO=0
简化结果为主矢和主矩都等于零，则原力系平衡，这种情形将在下节讨论。
（2）F′R≠0，MO=0
简化的结果为主矩为零，而主矢不为零。
就是原力系的合力，而合力的作用线恰好通过了特定的简化中心O。
（3）F′R=0，MO≠0
简化的结果为主矢为零，而主矩不为零。作用在简化中心的合力为零，但附加的力偶系并不平衡，可合成为一个力偶。因为力偶对于平面内任意点的矩都相同，因此当力系合成为一个力偶时，主矩与简化中心的选择无关。
（4）F′R≠0，MO≠0
简化的结果为主矢、主矩都不为零。这种情况还可以进一步简化，根据力的平移定理逆过程，可以把
和MO 合成一个合力FR。合成过程如图3-33 所示，合力FR 的作用线到简化中心O 的距离为
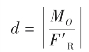
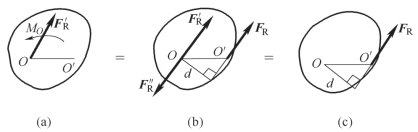
图3-33 简化结果F′R≠0，MO≠0
有关工程力学（第2版）的文章
- 详细阅读
-
平面任意力系的平衡方程及应用详细阅读
平面一般力系平衡的充分与必要条件是：力系的主矢和主矩同时为零。上式称为平面一般力系的平衡方程，平面一般的平衡方程有三个，可求解最多三个未知量。显然各力作用线在同一平面内且任意分布，属于平面一般力系。列平衡方程要根据物体所受的力系类型列出。比如，平面任意力系只能列出三个独立的平衡方程，平面汇交力系或平面平行力系只能列两个；平面力偶系只能列一个；对于由n 个物体组成的系统，可列出3n 个。......
2023-06-19
-
平面一般力系简化结果的讨论详细阅读
平面一般力系向一点简化，一般可得到一个力和一个力偶，但这并不是最后的简化结果。主矢、主矩均不为零，即在这种情况下，力系等效于一作用于简化中心O的力F′和一力偶矩为MO的力偶。合力F在O点的哪一侧，由F对O点的力矩的转向与主矩MO的转向相一致来确定。总之，对不同的平面任意力系进行简化，其最后结果只有三种可能性：一是合力；二是合力偶；三是平衡。......
2023-08-26
-
力系简化方法及其应用场景详细阅读
设在物体上作用有平面一般力系F1，F2，…，F′n可合成为一个作用于O点的力R′，并称为原力系的主矢[图4-5]，即图4-5力系的简化求主矢R′的大小和方向，可应用解析法。由于主矢等于原力系各力的矢量和，因此主矢R′的大小和方向与简化中心的位置无关。......
2023-06-16
-
平面表示方法介绍详细阅读
图3-33表示平面的方法2.用迹线表示平面平面与投影面的交线称为平面的迹线。图3-34用迹线表示平面平面迹线是平面与投影面的共有线，所以迹线的一个投影与它本身重合，其余投影必在相应的投影轴上，规定位于投影轴的投影省略不画。作图时只要分别求出它们的正面迹点和水平迹点，然后连接同面投影就可以把其他表示平面的方法转换成用迹线表示。......
2023-06-28
-
平面力系合成与平衡的方法分析详细阅读
平面汇交力系合成的几何法设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。若平面汇交力系有n 个力，用FR 表示合力矢，则有合力矢对刚体的作用与原力系对该刚体的作用是等效的。图3-17几何法求约束力根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。......
2023-06-26
-
解析法：另一种常用的求解平面汇交力系合成的方详细阅读
求解平面汇交力系合成的另一种常用方法是解析法。图2-3力的分解图2-4各力在坐标轴上的投影解：根据式（2-3）、式（2-4），列表计算如下：2.合力投影定理为了用解析法求平面汇交力系的合力，必须先讨论合力及其分力在同一坐标轴上投影的关系。图2-8例2-2图解析法。......
2023-06-16
-
平面一般力系合力矩定理详细阅读
于是可得到平面一般力系的合力矩定理。平面一般力系的合力对作用面内任一点的矩等于力系中各力对同一点的矩的代数和。因此，在平面力系情况下，固定端支座的约束反力包括三个：即阻止梁端向任何方向移动的水平反力XA和竖向反力YA，以及阻止物体转动的反力偶MA。试将这三个力向底面中心O点简化，并求简化的最后结果。......
2023-06-16
相关推荐