力的平移定理的应用和实现介绍

2023-06-19 理论教育版权反馈

【摘要】：显然，力F、F′和F" 组成的力系与原力F 等效。由图可见，附加力偶的力偶矩为力的平移定理表明，可以将一个力分解为一个力和一个力偶；反过来，也可以将同一平面内的一个力和一个力偶合成为一个力。应该注意，力的平移定理只适用于刚体，而不适用于变形体，并且只能在同一刚体上平行移动。图3-29力的平移力的平移定理不仅是力系向一点进行简化的依据，而且可以用来解释一些实际问题。

用两支桨划船，小船会直线前进，如图3-28（a）所示；而用一支桨划船，小船会在原地打转，无法前进，如图3-28（b）所示，这是不会划船的人容易出现的问题。这种现象如何解释？

pagenumber_ebook=54,pagenumber_book=45

图3-28　双桨划船和单桨划船示意图

由力的可传性知，力可以沿其作用线移到刚体上任意一点，而不改变力对刚体的作用效应。但当力平行于原来的作用线移动到刚体上任意一点时，力对刚体的作用效应就会改变，为了进行力系的简化，将力等效地平行移动，给出如下定理：

力的平移定理：作用于刚体上的力可以平行移动到刚体上的任意一指定点，但必须同时在该力与指定点所决定的平面内附加一力偶，其力偶矩等于原力对指定点的矩。

证明设力F 作用于刚体上A 点，如图3-29（a）所示。为将力F 等效地平行移动到刚体上任意一点B，根据加减平衡力系公理，在B 点加上两个等值、反向的力F′和F"，并使F′=F"=F，如图3-29（b）所示。显然，力F、F′和F" 组成的力系与原力F 等效。由于在力系F、F′和F" 中，力F 与力F" 等值、反向且作用线平行，它们组成力偶（F、F"）。于是作用在B 点的力F′和力偶（F、F"）与原力F 等效，即把作用于A 点的力F 平行移动到任意一点B，但同时附加了一个力偶，如图3-29（c）所示。由图可见，附加力偶的力偶矩为

力的平移定理表明，可以将一个力分解为一个力和一个力偶；反过来，也可以将同一平面内的一个力和一个力偶合成为一个力。应该注意，力的平移定理只适用于刚体，而不适用于变形体，并且只能在同一刚体上平行移动。

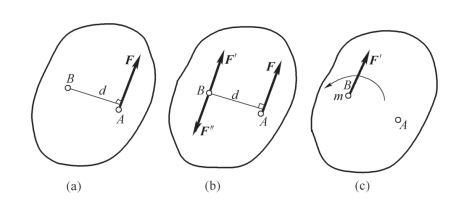
pagenumber_ebook=54,pagenumber_book=45

图3-29　力的平移

力的平移定理不仅是力系向一点进行简化的依据，而且可以用来解释一些实际问题。例如，前面讲的划船问题，可以用力的平移定理来解释。单桨划船，作用在桨上的力，向船的中心平移，得到一个力和一个力偶，所以船会在原地打转，而无法前进；而双桨划船，左右两桨上的力向船的中心平移，会得到一个合力，以及一对平衡的力偶，所以船会加速前行。钳工攻螺纹时必须用两只手同时均匀用力，以便产生力偶。如果只用一只手施力（图3-30），则作用在铰杠一端B 的力F 相当于一个作用在中点O 的力F′和一个附加力偶，这个附加力偶固然能起到攻螺纹的作用，但作用在中点O 的力F′却可能使丝锥折断。

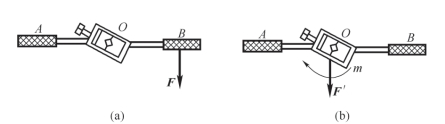
pagenumber_ebook=55,pagenumber_book=46

图3-30　丝锥攻螺纹

力的平移定理的应用和实现介绍

相关推荐