于是可得到平面一般力系的合力矩定理。平面一般力系的合力对作用面内任一点的矩等于力系中各力对同一点的矩的代数和。因此,在平面力系情况下,固定端支座的约束反力包括三个:即阻止梁端向任何方向移动的水平反力XA和竖向反力YA,以及阻止物体转动的反力偶MA。试将这三个力向底面中心O点简化,并求简化的最后结果。......
2025-09-29
在计算力系的合力对某点的矩时,有时力臂的计算较烦琐,而将合力分解计算各分力对某点的矩较简单。讨论合力对某点的矩和分力对该点的矩的关系,就是我们下面要讲述的合力矩定理。
定理:平面汇交力系的合力对其平面内任一点的矩,等于所有各分力对同一点的矩的代数和。
证明:设刚体上的A 点作用着一平面汇交力系,力系的合力为FR。在力系所在平面内任选一点O,过O 作Oy 轴,且垂直于OA。如图3-17 所示,则图中Ob1、Ob2、…、Obn 和ObR 分别等于力F1、F2、…、Fn 和FR 在Oy 轴上的投影F1y、F2y、…、Fny和FRy。现分别计算F1、F2、…、Fn 和FR 对点O 的力矩。
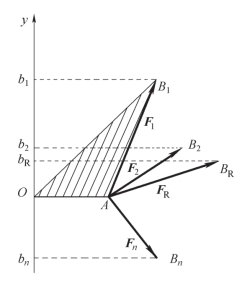
图3-17 力矩投影
由图3-17 可以看出
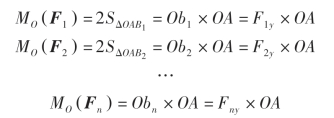
将上述等式两边相加,有
![]()
根据合力投影定理,有(https://www.chuimin.cn)
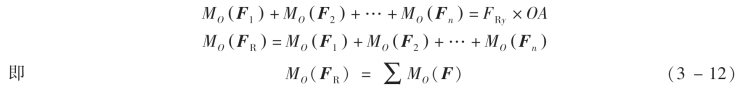
于是定理得到证明。对于有合力的其他各种力系,合力矩定理也是成立的。
案例3-7 作用于齿轮上的啮合力Fn=1 000 N,齿轮节圆直径D=160 mm,压力角(啮合力与齿轮节圆切线间的夹角)α=20°,如图3-18 所示。求啮合力Fn 对轮心点O 的矩。
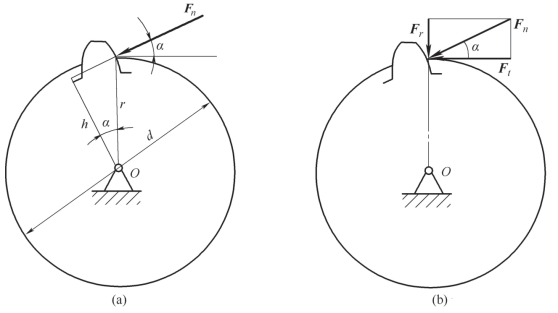
图3-18 案例3-7图
(a)直齿圆柱齿轮受力图;(b)齿轮受力分解图
分析:解法一 用力矩定义式(3-10)计算Fn 对点O 的矩,即

解法二 用合力矩定理式(3-12)计算Fn 对点O 的矩,如图3-18(b)所示,将啮合力Fn 在齿轮啮合点处分解为圆周力Ft 和径向力Fr,则Ft=Fncos α,Fr=Fnsin α,由合力矩定理可得

相关文章

于是可得到平面一般力系的合力矩定理。平面一般力系的合力对作用面内任一点的矩等于力系中各力对同一点的矩的代数和。因此,在平面力系情况下,固定端支座的约束反力包括三个:即阻止梁端向任何方向移动的水平反力XA和竖向反力YA,以及阻止物体转动的反力偶MA。试将这三个力向底面中心O点简化,并求简化的最后结果。......
2025-09-29

步进电动机定子有多相绕组,各相绕组依次通电。图7.3所示为三相反应式步进电动机原理,其定子有六个极,每极都装有控制绕组,每两个相对的极组成一相,六个极组成三相。步进电动机的绕组通电和断电一般由环形脉冲分配器控制。图7.3 步进电动机原理步进电动机每改变一次通电方式称为一拍,每拍通电转子转过的角度称为步距角θs。......
2025-09-29

例如:某照明灯的项目代号为“=S3+301-E3:2”,表示3号车间变电所301室3号照明灯的第2个端子。图1-33为某10kV线路过电流保护项目的项目代号、前缀及其分解图。图1-33 项目代号结构、前缀及其分解图1.高层代号对所给代号的项目而言,设备或系统中任何较高层次的代号都可称为高层代号。图1-34 位置代号说明示例图3.种类代号种类代号是用来识别项目种类的代号。端子代号是构成项目代号的一部分。......
2025-09-29

LED草坪灯是用于草坪周边的照明设施,也是重要的景观设施。图6-25 LED草坪灯常见的草坪灯主要利用太阳能电池的能源来进行工作,当白天太阳光照射在太阳能电池上,把光能转变成电能存贮在蓄电池中,再由蓄电池在晚间为草坪灯的LED提供电源。配有铁钎的LED草坪灯,直接通过铁钉插入泥土内即可,如图6-26a所示。有的太阳能LED草坪灯设计有灯具基座固定,如图6-26b所示,应使用不锈钢螺栓紧固。图6-26 太阳能LED草坪灯的安装......
2025-09-29

销主要用来固定零件之间的相对位置,称为定位销 ,它是组合加工和装配时的重要辅助零件;也可用于连接,称为连接销 ,可传递不大的载荷;还可作为安全装置中的过载剪断元件,称为安全销 。图3-8定位销图3-9连接销图3-10安全销销有多种类型,如圆柱销、圆锥销、槽销等,这些销均已标准化。定位销通常不受载荷,故不作强度校核计算,其直径可按结构确定,数目一般不少于两个。......
2025-09-29

现在来讨论怎样才能把力F平移到O点,而不改变其原来的作用效应。由此可得力的平移定理:作用在刚体上的力F,可以平移到同一刚体上的任一点O,但必须附加一个力偶,其力偶矩等于力F对新作用点O的矩。力F经平移后,它对柱子的变形效果就可以很明显地看出,力F′使柱子轴向受压,力偶使柱弯曲。......
2025-09-29
相关推荐