物体的受力分析及受力图制作

2023-06-19 理论教育版权反馈

【摘要】：受力分析时所研究的物体称为“研究对象”。这种解除了约束并被分离出来的研究对象，称为取“分离体”。将分离体所受的主动力和约束反力都用力矢量标在其相应的位置上，即得到分离体的受力图。梯子AC 部分的受力分析。在受力图上只需画出系统以外的物体给系统的作用力，这种力称为外力。

在工程实际中，为了求出未知的约束反力，需要根据已知力应用平衡条件求解。为此，要确定构件受了几个力，每个力的作用位置和力的作用方向。其次，还要确定哪些力是已知的、哪些力是未知的，最后根据平衡条件确定未知力的数值，这种分析过程称为物体的受力分析。

作用在物体上的力可以分为两类：一类是主动力，例如物体的重力、风力、气体压力等，一般是已知的；另一类是约束对物体的约束反力，为未知的被动力。

受力分析时所研究的物体称为“研究对象”。为正确进行受力分析，必须将研究对象的约束全部解除，并将其从周围物体中分离出来。这种解除了约束并被分离出来的研究对象，称为取“分离体”。将分离体所受的主动力和约束反力都用力矢量标在其相应的位置上，即得到分离体的受力图。上述过程称为“取分离体”“画受力图”，这是受力分析中的关键步骤。

绘制受力图，一般遵循以下步骤：

（1）根据问题的条件和要求，选择合适的研究对象，它可以是一个物体，也可以是几个物体的组合或整个系统。绘制出研究对象的简单几何图形，取分离体。

（2）先画出主动力，明确研究对象所受周围的约束，进一步明确约束类型。

（3）必要时需要用二力平衡共线、三力平衡汇交等条件确定某些反力的指向或作用线的位置。

注意：图中未画出重力的就是不计自重，没有提及摩擦时，则视为光滑面接触。

下面举例说明受力图的画法。

案例2-1 用一根绳索将放在光滑斜面上重为G 的球体连接到墙壁B 点[图2-27（a）]，画出球体的受力图。

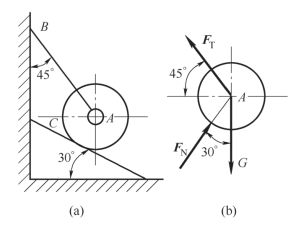
pagenumber_ebook=29,pagenumber_book=20

图2-27　案例2-1图

分析：（1）取球体为研究对象，解除绳索和光滑斜面约束，画出分离体。

（2）画主动力。在分离体上先画出主动力G。

（3）画约束反力。根据柔性约束反力应沿绳索的中心线并背离物体的性质，画出绳索拉力，再根据光滑面约束的约束反力应垂直于支撑面并指向物体的特性，画出相应的约束反力FN。

案例2-2 如图2-28（a）所示的三铰拱桥，由左、右两拱铰接而成。设各拱自重不计，在拱AC 上作用有载荷F。试分别画出拱AC 和CB 的受力图。

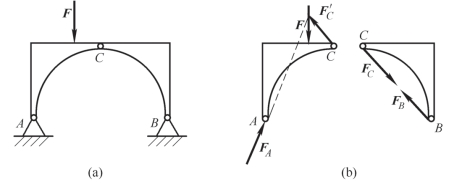
pagenumber_ebook=29,pagenumber_book=20

图2-28　案例2-2图

分析：（1）先分析拱BC 的受力。由于拱BC 自重不计，且只在B、C 两处受到铰链约束，因此拱BC 为二力构件。在铰链中心B、C 处分别受FB、FC 两力的作用，且FB=-FC，两个力的方向如图2-28（b）所示。

（2）取拱AC 为研究对象。由于自重不计，因此主动力只有载荷F。拱AC 在铰链C 处受拱BC 给它的约束反力F′C 的作用，根据作用力和反作用力定理，FC=-F′C。拱在A 处受固定铰链支座给它的约束反力FA 的作用，由于方向未定，暂可用两个大小未知的正交分力FAx、FAy代替。再进一步分析可知，由于拱AC 在F、F′C 和FA 三个力作用下平衡，故可根据三力平衡汇交定理确定铰链A 处约束反力FA 的方向。至于FA 的指向，暂且假定如图，以后可由平衡条件确定。

案例2-3 如图2-29 所示，画出梁AC 的受力图。

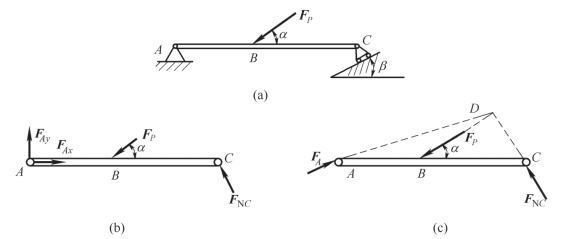
pagenumber_ebook=30,pagenumber_book=21

图2-29　案例2-3图

分析：

方法1——如图2-29（b）所示，以梁AC 为研究对象，梁AC 受到的主动力为FP，A端受固定铰链约束反力，可以用两个大小未知的力FAx、FAy 表示，C 端受可动铰链约束反力，其方向过铰链中心与支撑面垂直，用FNC表示。

方法2——如图2-29（c）所示，以梁AC 为研究对象，由于梁AC 在FP、FNC和FA 三力作用下平衡，故根据三力平衡汇交定理，可确定铰链A 处约束反力FA 的方向。D 点为力FP、FNC的交点，当梁AC 平衡时，约束反力FA 的作用线必通过D 点，至于FA 的指向，暂且如图2-29（c）所示，以后由平衡条件确定。

案例2-4 如图2-30（a）所示，梯子的两部分AB 和AC 在点A 铰接，又在D、E 两点用水平绳连接。梯子放在光滑的水平面上，若其自重不计，但在AB 的中点H 处作用一铅直载荷P。试分别画出绳子DE 和梯子的AB、AC 部分以及整个系统的受力图。

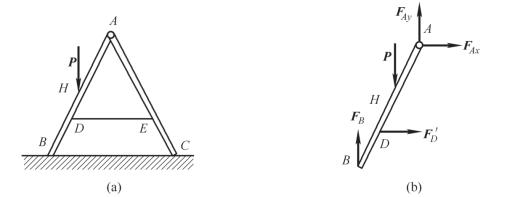
pagenumber_ebook=30,pagenumber_book=21

图2-30　案例2-4图

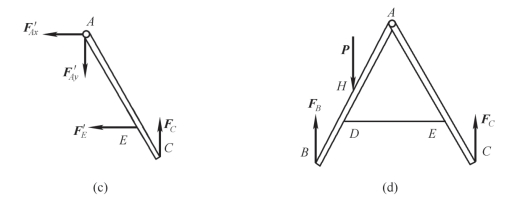
pagenumber_ebook=31,pagenumber_book=22

图2-30　案例2-4 图（续）

分析：（1）梯子AB 部分的受力分析。它在H 处受载荷P 的作用，在铰链A 处受AC 部分给它的约束反力FAx和FAy的作用，在点D 受绳子对它的拉力F′D，在点B 受光滑地面对它的法向反力FB 的作用。梯子AB 部分的受力图如图2-30（b）所示。

（2）梯子AC 部分的受力分析。在铰链A 处受AB 部分对它的作用力F′Ax和F′Ay（分别与FAx和FAy互为作用力和反作用力），在点E 受绳子对它的拉力F′E，在C 处受光滑地面对它的法向反力FC 的作用。梯子AC 部分的受力图如图2-30（c）所示。

（3）整个系统的受力分析。当选整个系统为研究对象时，可把整个平衡的结构看作刚体。由于铰链A 处所受的力互为作用力与反作用力，即FAx=-F′Ax，FAy=-F′Ay；绳子与梯子连接点D 和E 所受的力也分别互为作用力与反作用力，即F′D=-F′E，这些力都成对地作用在整个系统内，称为内力。内力对系统的作用效应相互抵消，并不影响整个系统的平衡，故内力在受力图上不必画出。在受力图上只需画出系统以外的物体给系统的作用力，这种力称为外力。这里，载荷P 和约束反力FB、FC 都是作用于整个系统的外力。整个系统的受力图如图2-30（d）所示。

应该指出，内力与外力的区别不是绝对的。例如，当我们把梯子的AB 部分作为研究对象时，F′Ax、F′Ay和F′E 均为外力，但取整体为研究对象时，FAx、FAy和F′E 又成为内力。可见，内力与外力的区别，只有相对于某一确定的研究对象才有意义。

物体的受力分析及受力图制作

相关推荐