公理2:二力平衡公理作用在刚体上的两个力使刚体处于平衡的充要条件是:这两力等值、反向且作用在同一直线上,如图1-3所示。图1-3二力平衡公理这个公理说明了作用在物体上的两个力的平衡条件,在一个物体上只受到两个力的作用而平衡时,这两个力一定要满足二力平衡公理。二力平衡公理中的两个力是作用在同一物体上的。此直杆称为二力杆。......
2023-06-16
公理是指人类在生活和生产实践中长期积累的经验总结,又经过实践反复检验,被确认是符合客观实际的最普遍、最一般的规律。
公理一 二力平衡公理
作用在同一个刚体上的两个力,使刚体保持平衡的充分和必要条件是:这两个力的大小相等,方向相反,并且作用在同一直线上,如图2-5 所示,简称这两个力等值、反向、共线,即
![]()
对于刚体,这个条件是其平衡的充分和必要条件。对于变形体,该条件仅是平衡的必要条件,但不是充分条件。例如,绳索受两个等值反向的拉力作用时可以平衡,而受两个等值反向的压力时就不能保持平衡。
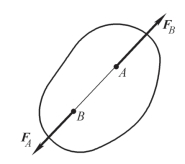
图2-5 二力平衡
在两个力的作用下处于平衡的物体称为二力体,若是杆件,则称为二力杆。由公理一可知,作用在刚体上的两个平衡力,它们必须通过两个力作用点的连线(与杆件形状无关),且等值、反向。如图2-6 所示。
这个公理表明了作用于刚体上的最简单的力系平衡时所必须满足的条件。
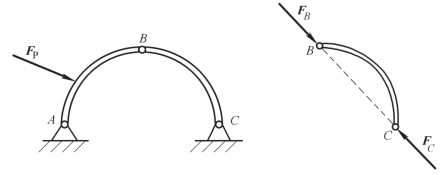
图2-6 二力构件
公理二 加减平衡力系公理
在作用于刚体的力系上,加上或减去任意平衡力系,并不改变原力系对刚体的作用效果。
也就是说,如果两个力系只相差一个或几个平衡力系,则它们对刚体的作用是相同的,因此可以等效替换。如图2-7 所示。
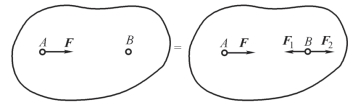
图2-7 加减平衡力系
这个公理是研究力系等效变换的依据。
公理三 力的平行四边形法则
作用在物体上同一点的两个力,可以合成为一个力。合力的作用点也在该点,合力的大小和方向由以这两个力为边构成的平行四边形的对角线确定,如图2-8 所示。或者说,合力矢量等于这两个分力的矢量和,即
![]()
应用此公理求两汇交力合力的大小和方向(即合力矢)时,可由任一点O 起,另作一力三角形,如图2-9 所示。力三角形的两个边分别为力矢F1 和F2,第三边FR 即代表合力矢,而合力的作用点仍在交汇点O。
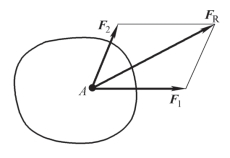
图2-8 力的平行四边形法则
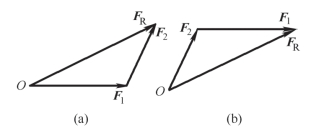
图2-9 力的三角形法则
这个公理表明了最简单力系的简化规律,它是复杂力系简化的基础。
公理四 作用力与反作用力公理
两个物体间的作用力和反作用力总是同时存在的,两力的大小相等,方向相反,作用在同一条直线上,且分别作用在两个物体上。
这个公理概括了物体间相互作用的关系,这表明了力是成对出现,且等值、反向、共线,但作用在两个物体上。
必须强调指出,由于作用力与反作用力分别作用在两个物体上,因此不能认为作用力与反作用力相互平衡。
推论一 力的可传性原理
作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,而不改变该力对刚体的作用。
证明:设有力F 作用在刚体上的点A,如图2-10 所示。根据加减平衡力系原理,可在力的作用线任取一点B,并加上两个相互平衡的力F′和F″,使F=F′=-F″,由于力F 和F″也是一个平衡力系,故可除去,这样只剩下一个力F′,于是,原来的这个力F 与力系(F,F′,F″)以及力F′等效,即原来的力F 沿其作用线移到了点B。
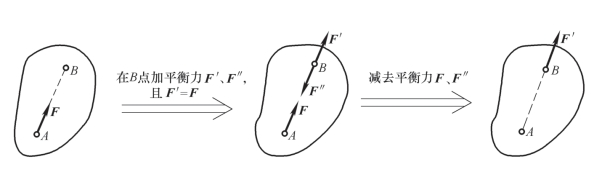
图2-10 力的可传性原理
由此可见,对于刚体来说,力的作用点已不是决定力的作用效果的要素,它已被作用线所代替,因此,作用于刚体上的力的三要素是:力的大小、方向和作用线。
推论二 三力平衡汇交定理
作用于刚体上的三个相互平衡的力,若其中两个力的作用线汇交于一点,则此三个力必须在同一平面内,且第三个力的作用线通过交汇点。
证明:如图2-11 所示,在刚体的A、B、C 三点上,分别作用三个相互平衡的力F1、F2 和F3。
根据力的可传递性,将力F1 和F2 移动到汇交点O,然后根据力的平行四边形法则得合力F,则F3 应与F 平衡。由于两个力平衡必须共线,所以力F3 必须与F1 和F2 共面,且通过力F1 和F2 的汇交点O。
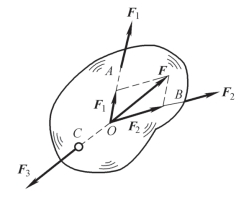
图2-11 三力平衡汇交定理
有关工程力学(第2版)的文章

公理2:二力平衡公理作用在刚体上的两个力使刚体处于平衡的充要条件是:这两力等值、反向且作用在同一直线上,如图1-3所示。图1-3二力平衡公理这个公理说明了作用在物体上的两个力的平衡条件,在一个物体上只受到两个力的作用而平衡时,这两个力一定要满足二力平衡公理。二力平衡公理中的两个力是作用在同一物体上的。此直杆称为二力杆。......
2023-06-16

在原来的正立投影面、水平投影面、侧立投影面三个基本投影面的基础上,增加了分别与它们平行的三个基本投影面,构成六面体方箱,将物体围在其中,这六面体的六个面均为基本投影面。各投影面展开时,规定正立投影面不动,其余各投影面按图6-1所示的方向,展开到与正立投影面在同一个平面上。图6-2六个基本视图的配置对于同一物体,并非要同时选用六个基本视图,至于选取哪几个视图,要根据物体的复杂程度和结构特点而定。......
2023-06-28

连接功能的实现主要涉及硬件技术,包括拓扑结构、控制方式、阻塞特性和故障防卫等方面的内容,下面分别进行简要说明。对T 接线器、S接线器、TST 网络及BANYAN 网络的详细介绍,可参阅第5.1.2节和第5.2.3节。这种系统不考虑阻塞率,但有时也可将等待时延超过门限值的呼叫视为被阻塞的呼叫。首先,在虚连接建立阶段遇到的阻塞与电路交......
2023-06-26

虽然托斯兰德所描述的团体工作主要涉及两种类型的团体,即治疗团体与任务团体,但是他关于工作过程的描述,对所有类型的团体都是适用的。以下结合托斯兰德对团体工作过程的论述,介绍与讨论团体工作的基本程序。根据斯托兰德的观点,在所有治疗团体的中期阶段,工作者应该开展四个方面的活动。......
2023-12-02

指针是C语言区别于其他同时代高级语言的主要特征之一。4)字符串C语言的字符串其实就是char型数组,所以使用字符串并不需要引用库。表达式3为循环控制变量修改表达式,它使for循环趋向结束。for循环语句是C语言中功能最为强大的语句,甚至在一定程度上可以代替其他的循环语句。......
2023-06-26

基本数据类型如表3-4所示。32位浮点数又称实数,浮点数表示的基本格式为1.m×2e,例如123.4可表示为1.234×102。图3-12所示为浮点数的格式,可以看出,浮点数共占用一个双字(32位),其最高位为浮点数的符号位,最高位为0时是正数,为1时是负数。浮点数的表示范围为-3.402823×1038~-1.175495×10-38,1.175495×10-38~3.402823×1038。Time数据类型以表示毫秒时间的有符号双精度整数形式存储。......
2023-06-15

图11.31MSTP的功能模型GFP:通用成帧规程 PPP:点到点协议 HDLC:高级数据链路协议LAPS:链路接入规程 RPR:弹性分组环MPLS:多协议标记交换能够支持的三类业务及其到VC的映射处理方法如下。MSTP 可适应多种网络拓扑,具有良好的可扩展性。......
2023-06-26
相关推荐