常用的确定随机数的方法有下面几种:1.用随机数骰子确定随机数用一个或多个骰子产生一位或多位数随机数。另外,在初值确定以后,所有的随机数就都被唯一确定下来了,不能满足真正随机数的要求。伪随机数需要通过一系列的统计检验,才能当做真正的随机数使用。这种方法产生随机数的周期比平方取中法有所改善,但还是周期不够长。......
2023-07-15
1.冷却数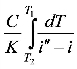 的计算
的计算
这里C为水的比热,取1kcal/kg·℃,K值由式(7-38)可求:
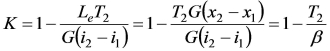
式中: ,K值变化关系可由图7-11查得
,K值变化关系可由图7-11查得
式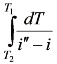 不能直接积分,可用梯形积分法近似计算,即在
不能直接积分,可用梯形积分法近似计算,即在 、
、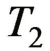 的区间内分成若干小区间,每段为
的区间内分成若干小区间,每段为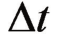 ,对应每个水温可以在焓湿图中查到,这样每个水温都可以求得
,对应每个水温可以在焓湿图中查到,这样每个水温都可以求得![]() 的值,将t作为横坐标,
的值,将t作为横坐标,![]() 作为纵坐标的点,以直线连接相邻的点形成一个以
作为纵坐标的点,以直线连接相邻的点形成一个以![]() 为高的梯形,这样梯形的面积之和就可以近似为
为高的梯形,这样梯形的面积之和就可以近似为 的值。
的值。
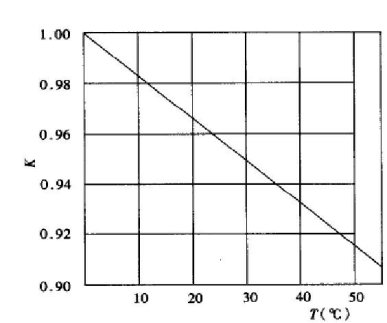
图7-11 T2—K曲线
由于冷却塔内气水处于热平衡状态,即有下式成立

式中符号同前,则有

假设在整个塔内该式成立,则有

式中T1、T2分别为进水温度和出水温度。
由式(7-49)可以求得每个温度下的空气焓值,因K值变化不大,以出塔温度T2为起点,以L/KG为斜率作一条直线,得到T~i的关系称之为空气操作线,它近似表示了进入塔内的空气与热水进行热交换后的焓值变化规律。同时在同一图上将饱和恰曲线画出,这样可以查到在同一温度下得i及i''。
2.特性数![]() 的计算与气水比
的计算与气水比
容积传质系数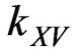 与塔结构、填料、空气条件、水力条件等因素有关,但在塔尺寸一定,填料一定时,其常用计算公式为:
与塔结构、填料、空气条件、水力条件等因素有关,但在塔尺寸一定,填料一定时,其常用计算公式为:
![]()
式中:g——空气流量密度,(kg/(m2·h));
q——淋水密度,(kg/(m2·h));
A,m,n——实验常数。
3.气水比的确定
冷却塔中冷却每公斤热水到达预定温度需要空气的公斤数称之为气水比。用 表示。
表示。

式中符号同前。
在冷却数N的计算中,i与 有关,所以冷却数N与
有关,所以冷却数N与 有关,而特性数
有关,而特性数 也与
也与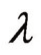 有关,因此可以通过先假设几个
有关,因此可以通过先假设几个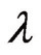 ,在同一张图上作出N—
,在同一张图上作出N— 及填料特性数
及填料特性数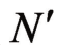 —
— 两条曲线,如图7-12所示,两曲线的交点D即所对应的气水比即所求的气水比。D即所对应的冷却数即设计气水比下的冷却数,D称为工作点。
两条曲线,如图7-12所示,两曲线的交点D即所对应的气水比即所求的气水比。D即所对应的冷却数即设计气水比下的冷却数,D称为工作点。 值选择范围见表7-1。
值选择范围见表7-1。
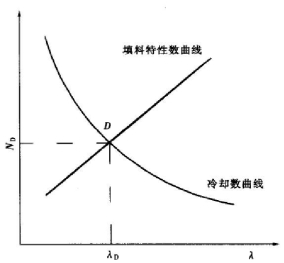
图7-12 气水比及冷却数的确定
表7-1 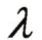 值选择范围
值选择范围

有关工业水处理技术的文章

常用的确定随机数的方法有下面几种:1.用随机数骰子确定随机数用一个或多个骰子产生一位或多位数随机数。另外,在初值确定以后,所有的随机数就都被唯一确定下来了,不能满足真正随机数的要求。伪随机数需要通过一系列的统计检验,才能当做真正的随机数使用。这种方法产生随机数的周期比平方取中法有所改善,但还是周期不够长。......
2023-07-15

为了得到扩散原子的散射截面,即<>,我们假设该扩散原子与图8.4所示的临近原子获得了扩散动能ΔHm,该参数独立于温度变量:那么,将式与式作比,则得出的就是散射截面的比值:式表明该比值和温度成反比。例如,在480℃下,对于铝的Z*的测量值和计算值分别为-30和-25.6。图8.5金原子的Z*随温度的变化关系我们可以从图8.4粗略地估计出,处于激发态的扩散原子的散射截面是正常原子的十倍左右,所以其有效电荷数大约等于10Z。......
2023-06-20

大约在3 000 多年前,中国古人就已形成了自然数概念,随后便掌握了自然数的运算法则。而在《九章算术》中,已对分数、正负数和无理数等概念均给出了明确而完整的描述。故同负数一样,中国古人对无理数的接纳显得非常从容和自然,且对于无理数的应用又是那样得心应手。在中国古代数学中,“面”常指平面图形的边,而这里则是指正方形的一边。“以面命之”意指将开方不尽的数借助“面”来表示。......
2023-11-23

(一) 截流时间的确定截流时间应根据枢纽工程施工控制性进度计划或总进度计划确定。如特殊情况必须在流冰期截流时应有充分论证,并有周密的安全措施。一般按频率法确定,根据已选定的截流时段,采用该时段内一定频率的流量作为设计流量。截流设计标准一般可采用截流时段重现期5~10 年的月或旬平均流量。......
2023-06-29

异养菌分为本身能从水质中摄取无机物或有机物而生活的腐生菌和依赖寄主供给营养的寄生菌两类。通常所说的异养菌指的是存在于水中的腐生菌。在循环冷却水中,异养菌不仅生长繁殖快,而且为数多,基本上代表了水中全部好氧菌的数量,所以一般在测定时,以这类细菌的数量作为细菌总数。循环冷却水中异养菌数的监测频率应为1次/周。对菌落计数用平皿计数法对异养菌的菌落进行计数,然后再计算每毫升水样中的异养菌数。......
2023-06-30

★ 首先我们来计算从1开始的连续自然数的和。+99+100=5050★ 现在我们来计算任意连续自然数的和。方法用上面的方法,计算从1到最后一个数的和。上面两个结果相减,即可。+1212×÷2=78再计算1+2+3+……+77×(7+1)÷2=28两式的差为78-28=50所以8+9+10+11+12=50计算11+12+13+……+20=210-55=155计算51+52+53+……+199+200=______计算18+19+20+21+22=______计算9+10+11+12+13+14+15=______计算50+51+……......
2023-10-27

将这些数值代入式中,我们可以得到对于铝的块体材料,取Z*=-26,则临界长度为3μm,其大小在数量级上是正确的,但是要小于实验测量的10~20μm。值得注意的是,临界长度可以利用实验方法测量长的铝条直接测出。在测量时,需要延长电迁移试验至足够长的时间,直到使得在阴极的质量传输或抑制作用停止为止。当ΔHmkT时,在分母中的“-1”项便可以忽略不计,化简后的等式表明临界长度对温度并不敏感。......
2023-06-20
相关推荐