首页 理论教育位置伺服控制系统稳态性能分析

位置伺服控制系统稳态性能分析

2023-06-19 理论教育 版权反馈
【摘要】：3）原理误差是由系统结构和位置控制器参数决定的，可以根据系统开环传递函数和位置信号性质分析。表7.4 位置伺服控制系统的典型输入信号从位置伺服控制系统传递函数包含的积分环节区分，伺服系统可以分为0型系统、Ⅰ型系统和Ⅱ型系统。

1.位置伺服控制系统的稳态误差

位置伺服控制系统的稳态性能主要是定位误差（准确度），定位误差包括检测误差、原理误差和扰动误差三方面：

1）检测误差主要由检测装置的准确度决定，是系统不能克服的误差，减小检测误差要采用高准确度检测装置，圆盘脉冲编码器定位准确度可以达到角秒（″）级，圆光栅定位准确度可以达到0.1″，长光栅为0.05μm。

2）扰动误差根据扰动的大小及加入的位置不同，产生误差的情况不同，需要具体情况具体分析。

3）原理误差是由系统结构和位置控制器参数决定的，可以根据系统开环传递函数和位置信号性质分析。

2.原理稳态误差分析

位置伺服控制系统从位置信号区分有定位控制和跟踪控制两类。定位控制位置指令是固定值，常用阶跃输入时的响应来衡量；跟踪控制位置指令随目标变动，如雷达对目标的跟踪等，跟踪控制常用速度、加速度和正弦等典型指令信号来衡量，见表7.4。

表7.4 位置伺服控制系统的典型输入信号

978-7-111-48427-1-Chapter07-24.jpg

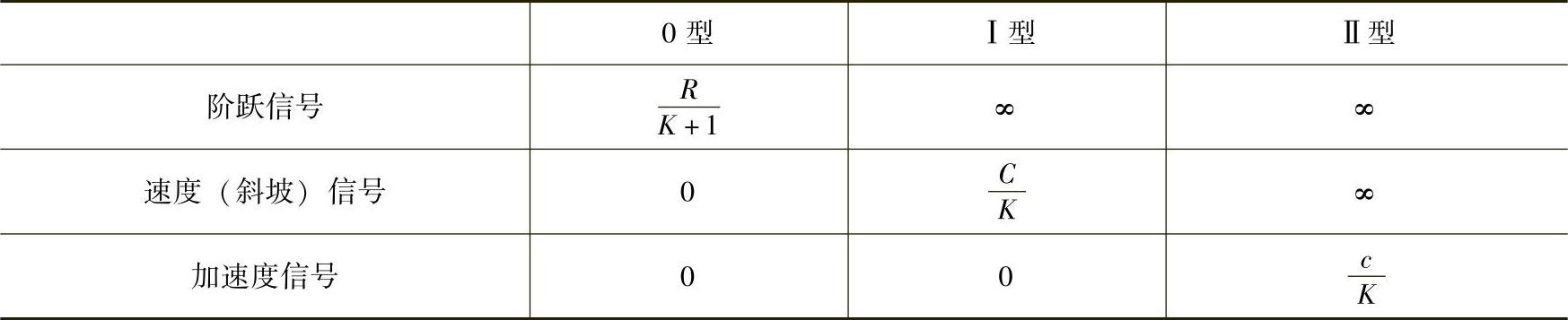
从位置伺服控制系统传递函数包含的积分环节区分，伺服系统可以分为0型系统、Ⅰ型系统和Ⅱ型系统。0型系统没有积分环节。Ⅰ型系统和Ⅱ型系统分别包含一个和两个积分环节。在阶跃信号、速度和加速度信号输入时，系统的稳态误差可以用拉普拉斯终值定理求得（见表7.5），但对正弦信号不能直接使用拉普拉斯终值定理，因为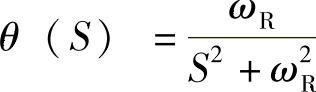978-7-111-48427-1-Chapter07-25.jpg含有右半平面的极点。求正弦输入信号时系统稳态误差有以下几种方法：

1）按误差公式计算，系统稳态误差为

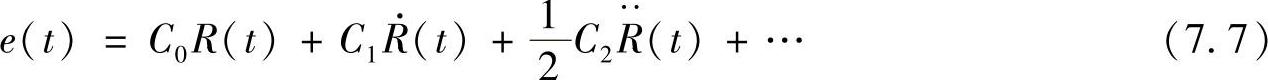
978-7-111-48427-1-Chapter07-26.jpg

式中

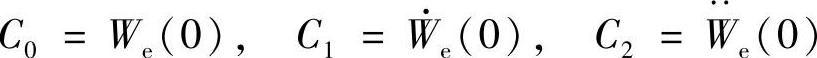
978-7-111-48427-1-Chapter07-27.jpg

We为误差传递函数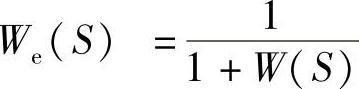，978-7-111-48427-1-Chapter07-28.jpg，W（S）为伺服系统开环传递函数。

表7.5 伺服控制系统典型输入时稳态误差（表中K为系统开环放大倍数）

978-7-111-48427-1-Chapter07-29.jpg

例7.1设伺服系统传递函数为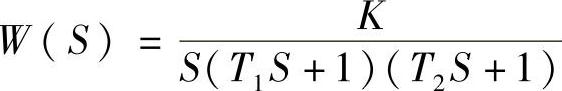978-7-111-48427-1-Chapter07-30.jpg，正弦输入信号为R（t）=RmsinωRt。

系统误差传递函数

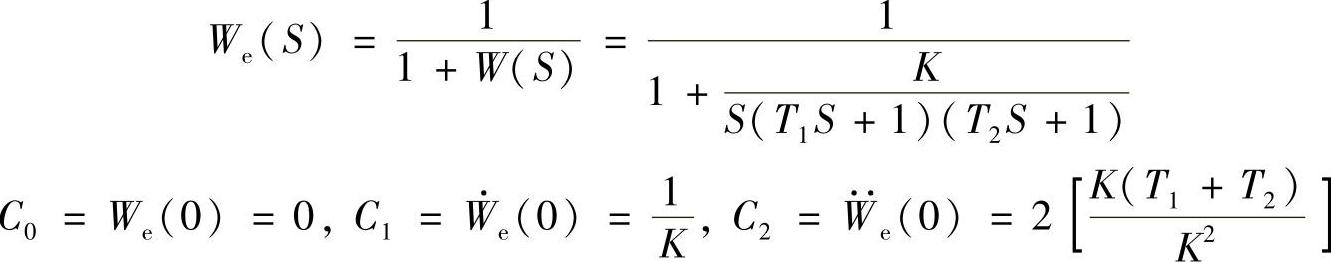
978-7-111-48427-1-Chapter07-31.jpg

代入式（7.5）可得

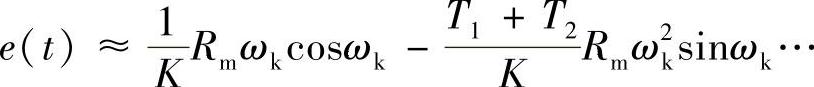
978-7-111-48427-1-Chapter07-32.jpg

所以系统在正弦输入信号时的稳态跟踪误差也是正弦函数，上式中，第1项为输入正弦信号的速度变化误差，第2项为输入正弦信号的加速度误差，其最大跟踪误差为

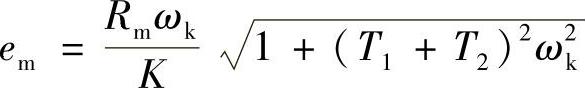
978-7-111-48427-1-Chapter07-33.jpg

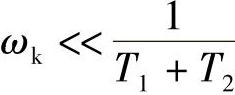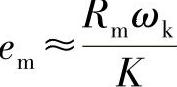在978-7-111-48427-1-Chapter07-34.jpg时，978-7-111-48427-1-Chapter07-35.jpg。

2）通过频率特性求稳态误差，即

978-7-111-48427-1-Chapter07-36.jpg

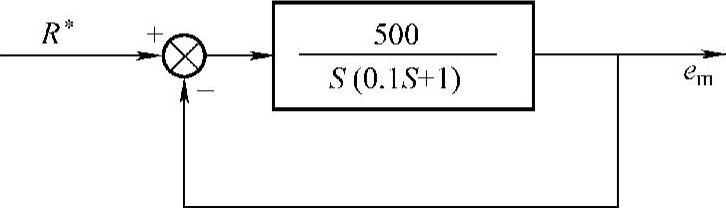
978-7-111-48427-1-Chapter07-37.jpg

图7.15 例7.2系统传递函数

例7.2已知系统结构如图7.15所示，前向通道传递函数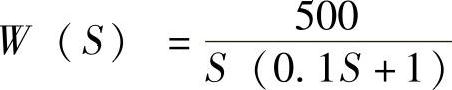978-7-111-48427-1-Chapter07-38.jpg，求：输入信号为R∗（S）≈sinωt，ω=5s-1时的稳态误差。误差频率特性为

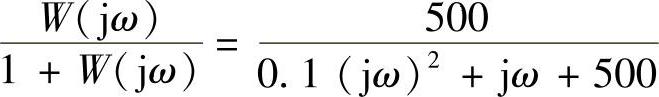
978-7-111-48427-1-Chapter07-39.jpg

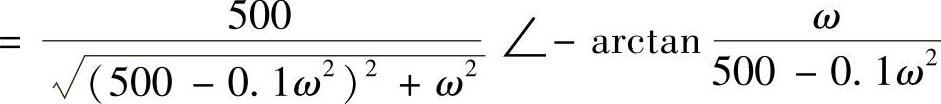
978-7-111-48427-1-Chapter07-40.jpg

在ω=5s-1时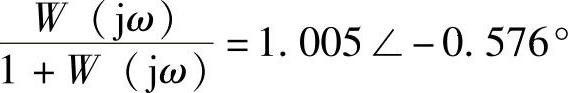，978-7-111-48427-1-Chapter07-41.jpg，则

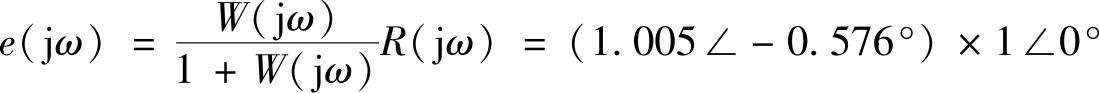
978-7-111-48427-1-Chapter07-42.jpg

稳态误差为

e（t）=sinωt-1.005sin（ωt-0.576°）=0.0112sin（ωt+116.1°）

有关电机运动控制系统的文章

  • 位置伺服控制系统的数学模型 位置伺服控制系统的数学模型

    位置伺服控制系统必有位置检测和位置控制器，位置控制器输出用于控制电动机，对于电动机又有转速开环和闭环控制，因此对于直流位置伺服控制系统，基本结构有：1）位置环+电枢调压调速。在各种位置闭环伺服控制系统中位置环是共有的，位置环内包含了电动机转速调节系统的等效传递函数和减速器和传动机构的传递函数，如图7.14所示。位置单闭环控制频带宽，响应快，一般用在小功率伺服系统中。......

    2023-06-19

    详细阅读
  • 位置伺服控制系统优化方案 位置伺服控制系统优化方案

    伺服控制系统是一种能够跟随输入指令信号进行控制的系统，也称随动控制系统。位置伺服控制系统用于机械的定位和定向控制，机器人、数控机床、雷达跟踪、舰船操舵等都大量使用电动机控制的位置伺服系统。位置闭环控制与调速系统的不同是其有位置检测和位置控制器。本章主要介绍步进电动机位置开环控制原理和伺服电动机位置闭环控制系统的组成和控制要求。......

    2023-06-19

    详细阅读
  • 位置闭环伺服控制系统的组成及优化 位置闭环伺服控制系统的组成及优化

    半闭环控制，减速器和丝杠间隙造成的误差在位置反馈环外，这些误差不能被抑制，因此控制准确度较全闭环控制低，但是成本低，安装和维护都比较方便。......

    2023-06-19

    详细阅读
  • 电液伺服控制系统的分析介绍 电液伺服控制系统的分析介绍

    电液伺服控制系统是以液压为动力，采用电气方式实现信号传输和控制的机械量自动控制系统。下面就以电液位置伺服控制系统为例，简要介绍一下电液伺服系统的组成和原理。电液伺服阀的作用是将小功率的电信号转换为阀的运动，以控制流向液压动力机构的流量和压力。电液伺服系统主要由电信号处理部分和液压的功率输出部分组成。图4－21电液伺服控制系统②反馈测量元件：测量系统的输出并转换为反馈信号。......

    2023-06-23

    详细阅读
  • 基于伯德图的系统稳态性能分析 基于伯德图的系统稳态性能分析

    系统的稳态性能是由系统的开环增益k和系统在原点的开环极点数N决定的，K和N一旦被确定，系统的稳态误差系数KP、KV、Ka也就被确定。在伯德图上是很容易确定K和N这两个参数的。根据开环系统对数幅频特性：在低频段，即认为，则对数幅频特性可写成L(ω)=20lgK-20×Nlgω显然，开环增益K和系统型数N的确定发生在低频段。由图可知，低频段斜率为零，其幅值为20lgK，则可以确定稳态位置误差系数KP。图5-47Ⅱ型系统对数幅频特性的低频部分......

    2023-06-28

    详细阅读
  • 静差转速闭环控制直流调速系统稳态性能分析 静差转速闭环控制直流调速系统稳态性能分析

    在图1.12所示转速负反馈调速系统中，若转速调节器采用比例调节器则组成转速闭环控制的有静差直流调速系统。B点所对应的转速高于A′点，即闭环控制后，电动机由负载增加引起的转速降减小。因此，采用比例调节器的闭环控制系统必然是有静差调速系统，提高放大倍数KP可以减小偏差，但是不能消除偏差，而且放大倍数过大还会引起系统的不稳定。图1.14 开环和闭环控制静特性......

    2023-06-19

    详细阅读
  • 控制系统性能指标方法的分析介绍 控制系统性能指标方法的分析介绍

    图3-7系统的单位阶振荡跃响应及性能指标图3-8系统的单位阶跃单调响应及性能指标常用的动态性能指标如下所述。......

    2023-06-28

    详细阅读
  • 稳态调速性能指标的优化方法 稳态调速性能指标的优化方法

    图2-2典型阶跃响应曲线和跟随性能指标图2-3突加负载时的动态过程和抗扰性能指标......

    2023-06-25

    详细阅读