采用均相流模型中的质量输运空化模型，形式［141］如下：式中，分别表示质量蒸发速率和质量凝结速率；αν为空泡体积分数；ρν为汽体密度，其值为0.554 kg/m3。质量输运空化模型的质量蒸发速率和质量凝结速率，大多数为在Rayleigh-Plesset方程的基础上推导出来的，其形式为：式中，Rb为空泡平均半径，其值为10-6 m；ρl为液体密度，其值为997 kg/m3；pν为饱和蒸汽压力，其值为3 574 Pa；S为液体的表面张力；μ为液体的动力黏性系数。......
2025-09-29
异步电动机在一个二相任意旋转坐标系上的模型
【摘要】：建立一个二相旋转的坐标系dq，dq坐标系的旋转速度为ωdq，ωdq是可以任意规定的，因此称为二相任意旋转坐标系。图4.6 异步电动机在二相任意旋转坐标系上的动态等效电路异步电动机在任意旋转dq坐标系上模型的特点如下：1）在dq坐标系上异步电动机的电压方程是四维的，变量比三相模型减少，但方程的阻抗矩阵仍是满秩的，其非线性、多变量、强耦合的性质还没有完全改变。
二相交流电动机模型定子和转子分别建立在两个静止坐标系上，电压方程由三相电动机的六个减少为四个，电压和电流变量也减少了，但是定子绕组和转子绕组间的复杂耦合关系并没有改变，如果将二相交流电动机模型的两个坐标系通过旋转变换（2s/2r）统一到一个旋转坐标系上，则可以减少定子和转子绕组之间的耦合关系，使电压方程进一步简化。
建立一个二相旋转的坐标系dq（见图4.4c），dq坐标系的旋转速度为ωdq，ωdq是可以任意规定的，因此称为二相任意旋转坐标系。采用2s/2r变换，将二相静止坐标系αsβs上电动机（见图4.4b）的两个定子绕组变换到二相任意旋转坐标系dq上（见图4.4c），并且将αrβr静止坐标系上的两个转子绕组也变换到同一个dq坐标系上，这样得到了在一个dq坐标系上的二相电动机模型。建立在同一dq坐标系上的二相电动机模型的特点如下：
1）在二相电动机模型中有两个坐标系，定子αsβs坐标系是静止的，转子αrβr坐标系相对转子是静止的，相对定子αsβs坐标系是旋转的。在dq坐标系上电动机模型的定子和转子都是旋转的，定子相对于原定子αsβs坐标系的旋转速度为ωdqs=ωdq-0=ωdq，转子相对于原转子αrβr坐标系的旋转速度为ωdqr=ωdq-ω。
2）由式（4.29）和式（4.30），变换后在dq坐标系上定子电流的频率为（ω1-ωdq）。将式（4.29）和式（4.30）用于转子电流变换时，原转子αrβr坐标系上的电流频率为ωs，dq坐标系相对转子αrβr坐标系的转速为（ωdq-ω），因此变换到dq坐标系上转子电流频率为[ωs-（ωdq-ω）]=ω1-ωdq，即变换到同一个dq坐标系上后，转子和定子电流频率相同，电压频率也相同。
3）定子和转子的两个绕组在同一轴线上（d轴和q轴）随轴旋转，同轴定子和转子绕组之间没有相对运动，互相的关系是静止的，但实际转子绕组相对定子绕组是旋转的，因此这种静止仅是假象，称为“伪静止”，而转子的旋转将在电压方程中以旋转电动势表示。
4）从两个静止二相坐标系到一个旋转二相坐标系的变换，仅是数学表达形式的变化，电动机的本质没有变，因此从三相到二相的电动机参数变换关系[见式（4.39）～式（4.41）]也适用于旋转二相坐标系的电动机模型。
1.在dq坐标系上的磁链方程
在任意旋转dq坐标系上，“伪静止”的同轴定子和转子绕组之间有互感Lm，但d轴绕组与q轴绕组互相垂直，即它们之间的互感为0，这意味着d轴绕组与q轴绕组互不影响（解耦）。因此可以写出在dq坐标系上的磁链方程
Ψsd=Lsisd+Lmird
Ψsq=Lsisq+Lmirq
Ψrd=Lrird+Lmisd
Ψrq=Lrirq+Lmisq （4.42）或
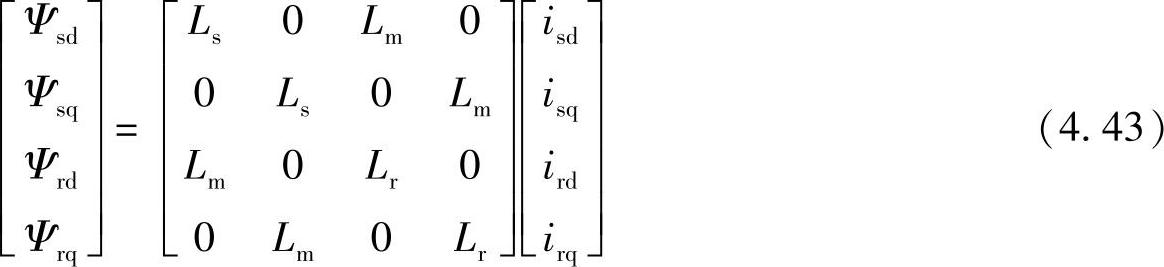
2.dq坐标系上的电压方程
在dq旋转坐标系上定、转子绕组之间没有相对运动，但这仅是伪静止，定、转子绕组电压中除电流变化产生的脉动电动势pΨ外，还包含着转子旋转产生的旋转电动势ωΨ，在dq坐标系上，该旋转以定子和转子对dq坐标系的相对速度ωdqs和ωdqr表示，定子旋转角频率ωdqs=ωdq-0=ωdq，转子旋转角频率ωdqr=ωdq-ω，因此异步电动机在dq坐标系上的电压方程为
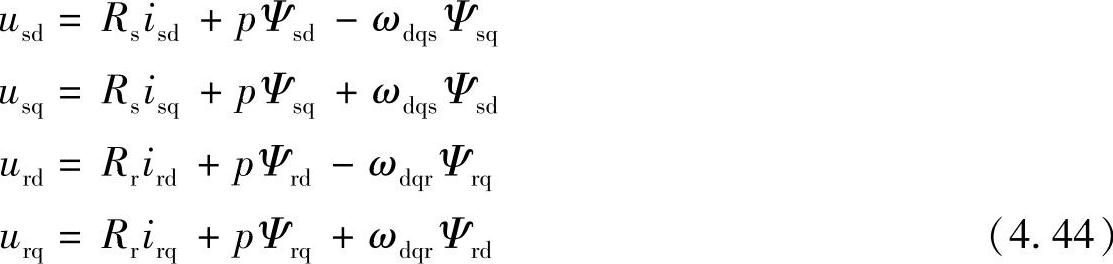
将电流和磁链代入各相电压方程，得
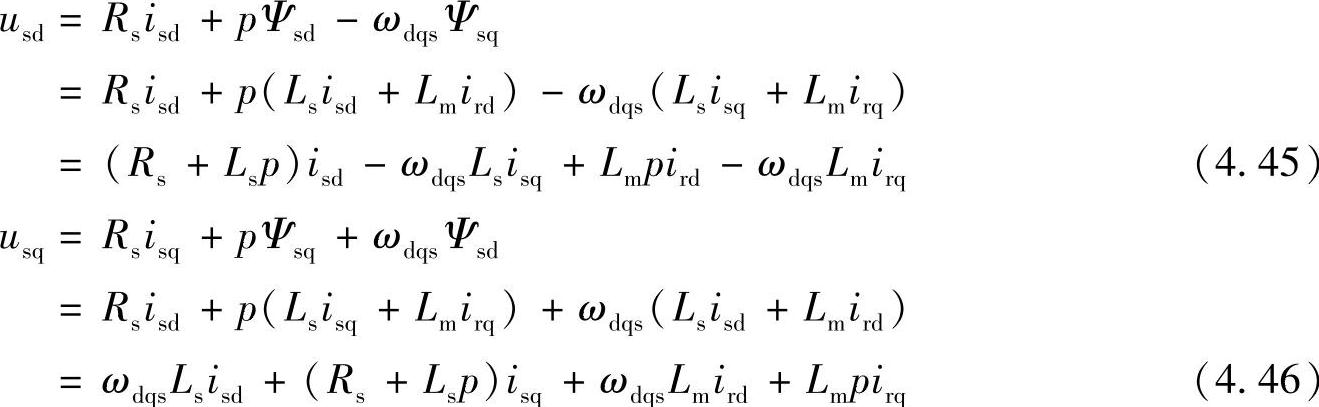(https://www.chuimin.cn)
同理可得转子电压方程
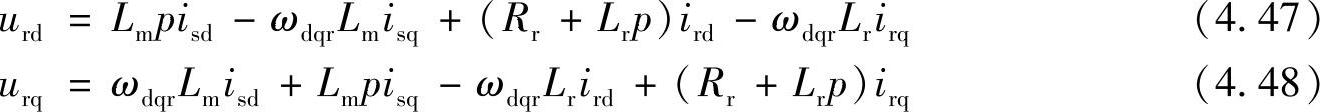
整理定子和转子电压方程可得，在任意旋转dq坐标系上电压方程的矩阵形式为
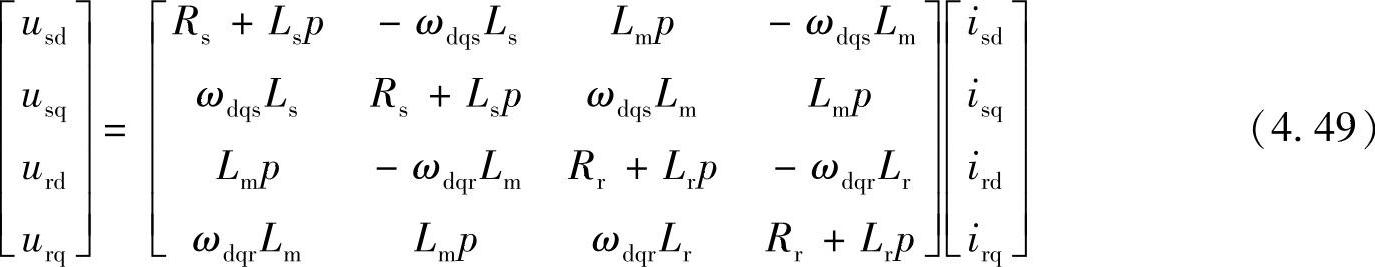
3.dq坐标系上电动机的转矩方程
dq坐标系上电动机的转矩方程为Te=npLm（isqird-isdirq） （4.50）
4.电动机的运动方程
电动机的运动方程为
5.异步电动机动态等效电路
在dq坐标系上的电压方程中，定子和转子的电压和电流有相同的频率，因此根据电压方程[见式（4.49）]可以画出二相异步电动机的T形动态等效电路，如图4.6所示。因为是动态等效电路，所以电压和电流为瞬时值，等效电路由d轴和q轴两部分组成。d轴和q轴等效电路的基本结构相同，不同之处在旋转电动势项的方向。旋转电动势项ωdqsLm和ωdqrLm反映了负载和转速对电动机动态的影响，包含旋转电动势项也是电动机动态等效电路与稳态等效电路（见图3.16）的主要区别。
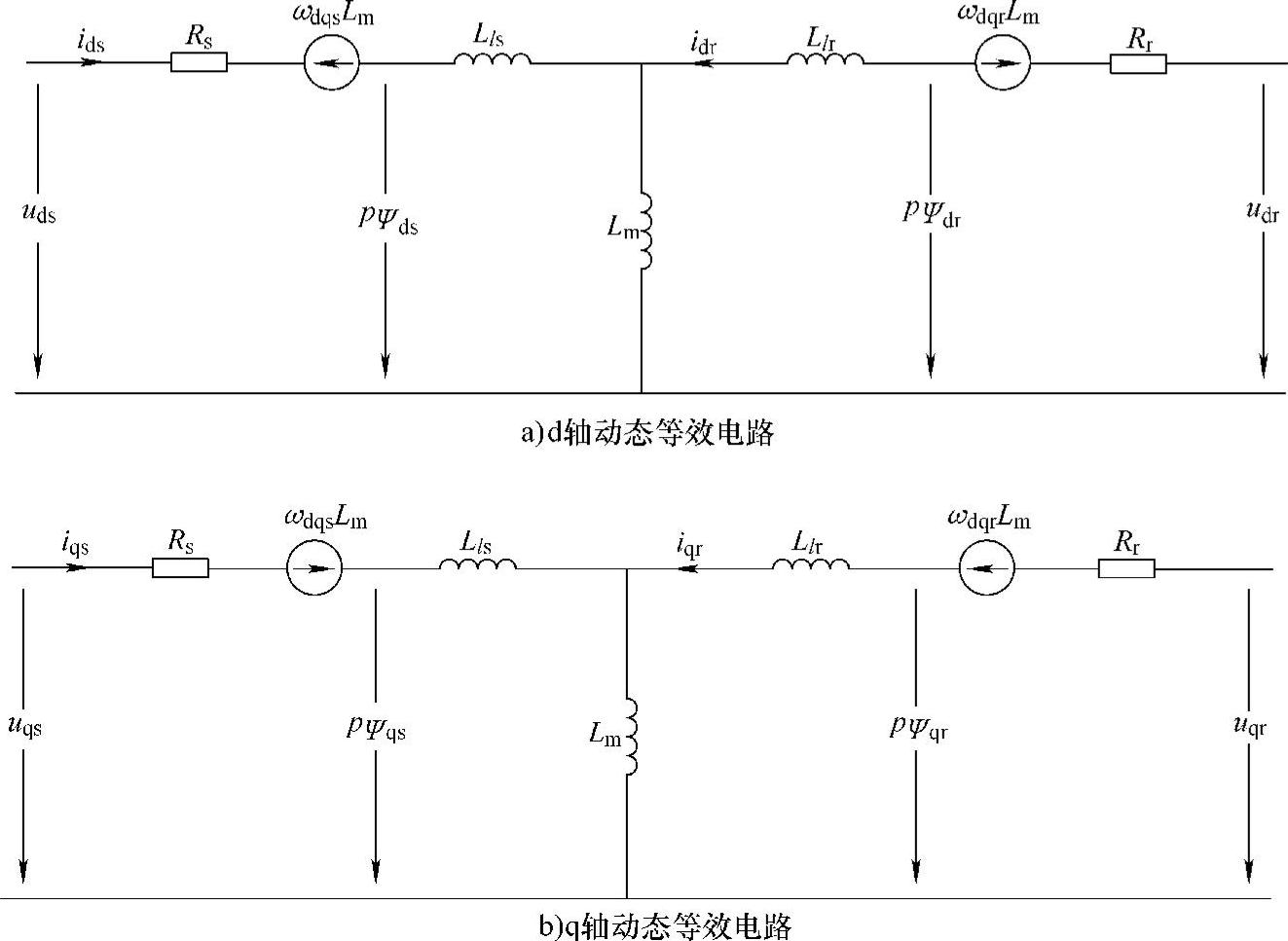
图4.6 异步电动机在二相任意旋转坐标系上的动态等效电路
异步电动机在任意旋转dq坐标系上模型的特点如下：
1）在dq坐标系上异步电动机的电压方程是四维的，变量比三相模型减少，但方程的阻抗矩阵仍是满秩的，其非线性、多变量、强耦合的性质还没有完全改变。
2）dq坐标系的旋转速度是任意的，因此式（4.49）的电压方程具有一般性，定义dq坐标系的旋转速度可以得到不同形式的电压方程，可以从不同视角研究不同的问题。
3）在dq坐标系上电动机定子和转子电压电流的频率相同，而且频率随dq坐标系的旋转速度变化。稳态模型（见图3.1b）中，定子和转子频率也相同，但为ω1。
相关文章
- 详细阅读
-
异步电动机稳态数学模型优化详细阅读
图3.1a所示模型中转子和定子的频率不同，转子和定子回路之间由互感联系，不便于计算，一般通过频率折算、绕组折算和磁通折算得到异步电动机的等效模型，如图3.1b所示。电动机定子互感电动势Esm和转子互感电动势Erm的关系为Eg=Esm=keErm （3.6）其中式中，N1、N2分别为定子和转子一相绕组匝数；kW1、kW2分别为定子和转子的绕组系数。......
2025-09-29
-
异步电动机稳态数学模型与调速控制系统详细阅读
异步电动机旋转是由于气隙磁场与转子电流的互相作用，因此气隙磁场和转子电流是异步电动机控制的两个重要参数。本章在异步电动机的稳态数学模型基础上研究异步电动机的调速方法，分析各种调速方法的电动机调速性能，并介绍异步电动机稳态控制系统的仿真研究。异步电动机的动态数学模型及矢量控制将在第4章介绍。......
2025-09-29
-
随机森林模型的原理详解详细阅读
另外，随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法，因此CART方法与装袋算法结合就形成了随机森林算法，可以提高模型预测准确率。随机森林模型中某一特征的重要性，是所有决策树得到的该特征重要性的平均值。......
2025-09-29
-
建立操作机构仿真模型的优化方法详细阅读
通过ADAMS软件提供的图形接口模块，将三维实体造型软件UG中建立的机构三维模型导入到ADAMS软件中的。考虑到所关心的问题和仿真的方便，对操作机构作适当简化后，用ADAMS软件包建模。约束关系的添加要充分考虑实际操作机构中可能存在的约束，遗漏任何一个约束关系都会严重影响到输出结果。3）仿真过程的控制 在ADAMS软件中，为了实现对仿真过程的控制，需要添加传感器来控制仿真过程的自动终止。......
2025-09-29
-
优化载荷子输运模型的研究详细阅读
单极电荷的输运的数学公式已经被提出。目前，仍未出现同时考虑双极电流、输入受限输运和整体受限输运的统一模型。空穴输运在低能级上完成，所以空穴对因氧气等环境因素而产生的陷阱不敏感。相反，电子对距离较近的这类陷阱敏感并总是表现出弥散输运行为。该理论对OLED的输运描述而言是有价值的。同时，其他研究小组保留了SCLC理论的有效性，并且将迁移率与电场的关系包含在内，这种关系目前是强制性的。......
2025-09-29
-
杀伤增强模型的优化技术详细阅读
图6.42装填系数对预制破片初速的影响不同口径的随进子弹破片初速轴向分布如图6.43所示。图6.46不同口径的随进子弹破片分布密度4.破片有效杀伤距离破片在空中飞行的过程中，速度不断衰减，依靠其存速或剩余动能杀伤距离R处的目标。随进子弹口径从35 mm增大至50 mm，破片有效杀伤距离增加60%～70%。......
2025-09-29
-
毁伤增强模型的优化方案详细阅读
图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀，裂纹内气体体积可表述为式中，a为裂纹长度；W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点，爆燃反应冲击波呈球形在跑道各层介质中传播，产生径向压力波，强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中，A为混凝土面层反射系数。......
2025-09-29
相关推荐