一般将二相坐标系的α轴放在三相坐标系的A轴上，如图4.2所示，将三相磁动势FA、FB、FC投影到二相坐标系的α和β轴上，可以建立二相绕组与三相绕组的磁动势等效关系即以矩阵形式表示为并且二相/三相的变换关系为式中可以证明，C3s/2s、C2s/3s既是电流的变换矩阵，也是电压和磁链的变换矩阵。从式还可以看到，在二相静止坐标系上，二相电流iα、iβ的相位差为。......
2023-06-19
二相静止坐标系和旋转坐标系的变换方法（2s/2r变换）
【摘要】：将图4.3中的合成磁动势F分别投影到两个坐标系上，可以建立两个坐标系的变换关系式中C2s/2r是电流从二相静止到二相旋转坐标系的变换矩阵，C2r/2s是从二相旋转到二相静止坐标系的变换矩阵，C2s/2r和C2r/2s互为转置矩阵和逆矩阵，且C2s/2r和C2r/2s也是电压和磁链在二相静止和二相旋转坐标系变换时的变换矩阵。图4.3 2s/2r坐标变换设：，且φ=ωdqt，φ0=0，代入式，得式和式说明，二相旋转坐标系上，id和iq的幅值与静止αβ坐标系上绕组的电流幅值相同。
二相对称绕组通以二相对称电流可以产生旋转磁场F，如果二相电流的角频率为ωs，则产生磁动势F的旋转速度（以角频率表示）也是ωs，如果让二相绕组转起来，旋转的速度为ωdq，则磁动势F的旋转速度是（ωs+ωdq）。在图4.3中建立了两个坐标系，两个坐标系轴上都有匝数为N2的绕组，αβ坐标系是不旋转的静止坐标系，dq坐标系是旋转的坐标系，它相对于静止αβ坐标系的旋转速度为ωdq。两个坐标系之间的转角为φ，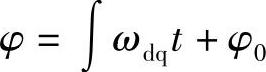
，其中ωdq为dq坐标系相对于αβ坐标系的旋转速度，φ0为t=0时dq坐标系对αβ坐标系的初始角。Fα和Fβ是静止αβ坐标系上两个绕组产生的轴向磁动势，F是它们的合成旋转磁动势，磁动势F的旋转速度为ω1。将在dq旋转坐标系上的两个绕组产生的轴向磁动势记为Fd和Fq，两个绕组通过角频率为ωs的电流id和iq，则Fd=N2id，Fq=N2iq，其合成磁动势幅值同为F。F的旋转速度相对于dq坐标系为ωs，相对于αβ坐标系为（ωs+ωdq），若ωs+ωdq=ω1，则按磁动势相等的原则，静止αβ坐标系上绕组的作用可以用dq旋转坐标系上的绕组来等效。将图4.3中的合成磁动势F分别投影到两个坐标系上，可以建立两个坐标系的变换关系
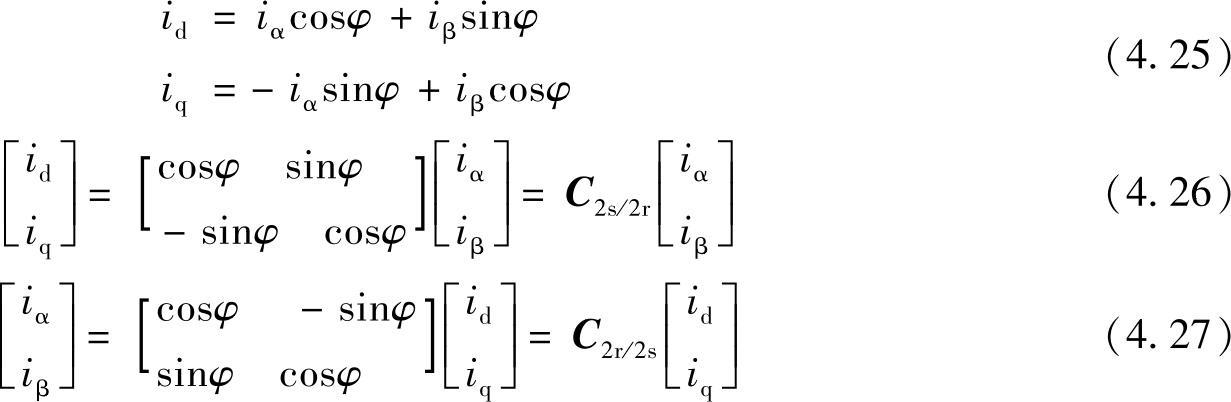
式中
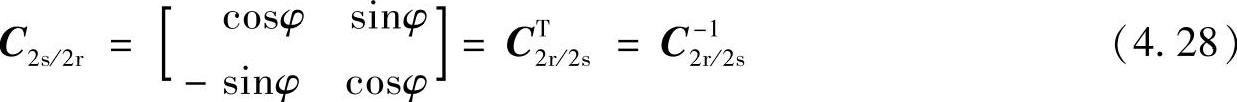
C2s/2r是电流从二相静止到二相旋转坐标系的变换矩阵，C2r/2s是从二相旋转到二相静止坐标系的变换矩阵，C2s/2r和C2r/2s互为转置矩阵和逆矩阵，且C2s/2r和C2r/2s也是电压和磁链在二相静止和二相旋转坐标系变换时的变换矩阵。因为
，所以在进行2s/2r和2r/2s变换时不仅需要已知dq坐标系的旋转速度ωdq，还需要确定dq坐标系的初始位置φ0，确定dq坐标系的φ角称为dq坐标系的定向。
图4.3 2s/2r坐标变换
设：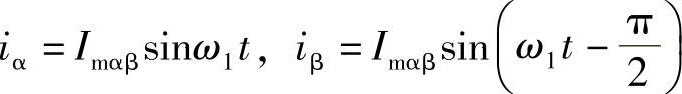
，且φ=ωdqt，φ0=0，代入式（4.25），得
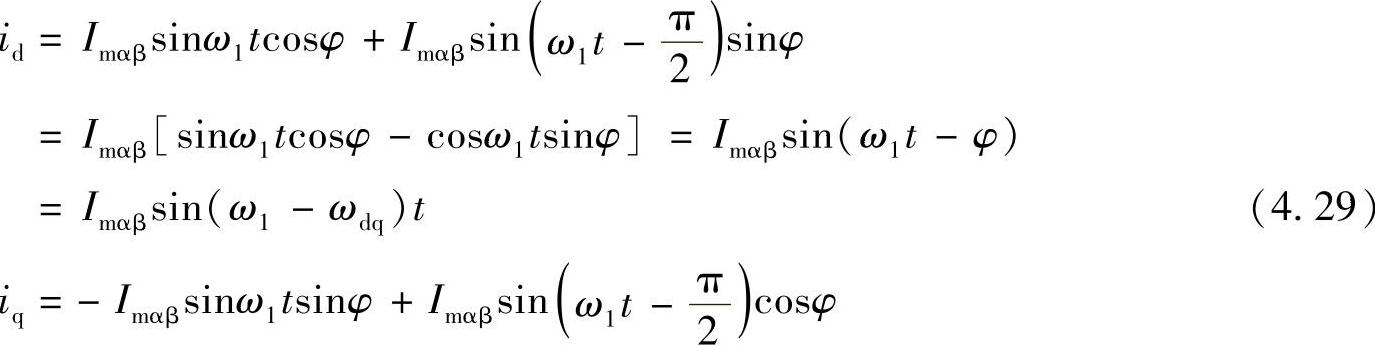
式（4.29）和式（4.30）说明，二相旋转坐标系上，id和iq的幅值与静止αβ坐标系上绕组的电流幅值相同。若id和iq的频率为ωs，则有ωs=ω1-ωdq，ωs随dq坐标系的旋转速度ωdq而变化，在ωdq=ω1时，ωs=0，即dq坐标系上两个绕组的电流为直流电。
有关电机运动控制系统的文章
- 详细阅读
-
如何进行坐标变换？- 从静止坐标系到旋转坐标详细阅读
在实际进行3S/2S变换时，也可以按照式（7-6）的形式进行计算，不会影响变换结果，即根据式可求出反变换即2S/3S变换的变换矩阵在实际进行2S/3S变换时，也可以写成图7-3两相静止和旋转坐标系的磁通势空间矢量2.2S/2R变换从两相静止坐标系αβ到旋转坐标系MT之间的等效变换称为2S/2R变换，其中S表示静止，R表示旋转。其中αβ坐标系是静止的，MT坐标系以角速度ω1旋转，M轴与α轴之间的夹角φ随时间变化。......
2023-06-25
-
平面直角坐标系中的位似变换探讨详细阅读
在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点（x，y）对应的位似图形上的点的坐标为_________．1．在平面直角坐标系中，△ABC与△A′B′C′是以原点为位似中心的位似图形，若点A和它的对应点A′的坐标分别为（－4，2），（8，－4），则△ABC与△A′B′C′的相似比是（ ）．2．如图，△ABC和△A′B′C′位似，位似......
2023-07-03
-
建立与选择工件坐标系的方法和技巧详细阅读
图2.2-8 工件坐标系的转换FS-0iMD扩展工件坐标系可用指令G54.1或G54选择，指令格式如下：n为扩展工件坐标系序号，可输入1～48。......
2023-06-25
-
相关变换：相切变换操作详解详细阅读
选取图13.2.31所示的模型表面为要组合的面。下面以图13.2.34所示的模型为例介绍相切变换操作的一般过程。图13.2.34 相切变换Step1.打开文件D：\ug90\work\ch13.02.08\maketangent.prt。图13.2.35 “设为相切”对话框图13.2.36 选取曲面对象Step5.单击对话框中的按钮，完成相切变换操作。Step2.选择下拉菜单命令，系统弹出图13.2.38所示的“设为对称”对话框。......
2023-11-20
-
坐标系统和计算网格详解详细阅读
5.5.4.3自适应计算网格生成河床及河岸的冲淤与其附近区域的水沙运动有十分密切关系，要求河道演变数学模型对河床及河岸附近流场和含沙场有较高的分辨率，采用固定网格会造成边岸有效网格呈现出阶梯状分布而降低河床和边岸附近的计算精度。......
2023-06-22
-
坐标变换与变换矩阵详细阅读
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2023-06-19
-
卡洛变换详解详细阅读
离散卡-洛变换是根据信号的统计特性性质进行正交展开。由式表示的变换称为离散卡-洛变换，系数向量g是信号向量通过该正交变换得到的，称之为主成分信号向量。离散卡-洛变换主要用于遥感多光谱信号中特征选择及数据压缩方面。因为是λi单调递减的，如果所选M个特征向量与M个最大特征值对应，那么用式来重建信号向量的误差最小，所以在最小均方误差的意义上讲，离散卡-洛变换是最优的。......
2023-06-23
相关推荐