【摘要】:一般将二相坐标系的α轴放在三相坐标系的A轴上,如图4.2所示,将三相磁动势FA、FB、FC投影到二相坐标系的α和β轴上,可以建立二相绕组与三相绕组的磁动势等效关系即以矩阵形式表示为并且二相/三相的变换关系为式中可以证明,C3s/2s、C2s/3s既是电流的变换矩阵,也是电压和磁链的变换矩阵。从式还可以看到,在二相静止坐标系上,二相电流iα、iβ的相位差为。
三相对称绕组通以三相电流iA、iB、iC,即
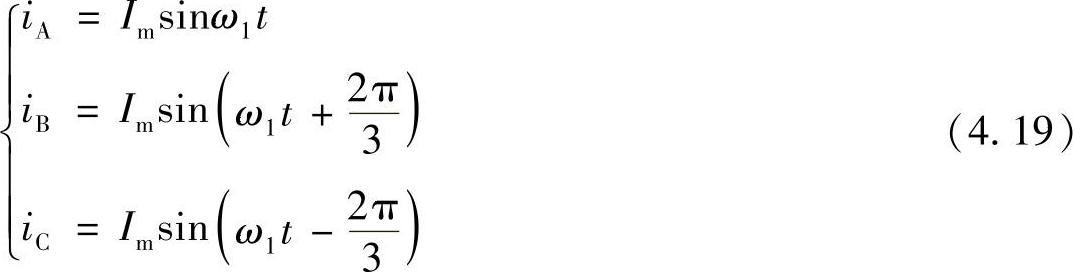
三相电流分别在三相坐标系ABC的轴线上产生三相磁动势FA、FB、FC,如图4.2所示,FA=N3iA,FB=N3iB,FC=N3iC。式中,N3为三相绕组匝数。磁动势FA、FB和FC是不旋转的,它们仅沿三相轴线上有大小的变化,但是它们产生的合成磁动势F是旋转的空间矢量,其旋转角速度为ω1,ω1=2πf1(f1为电流频率)。除一相外,二相、三相、四相、五相……等任意相对称绕组通以相应的对称电流都可以产生旋转磁动势(旋转磁场)。其中最简单的是二相。二相对称绕组的特点是,两个绕组互相垂直(正交),二相对称电流的相位互差90°,即

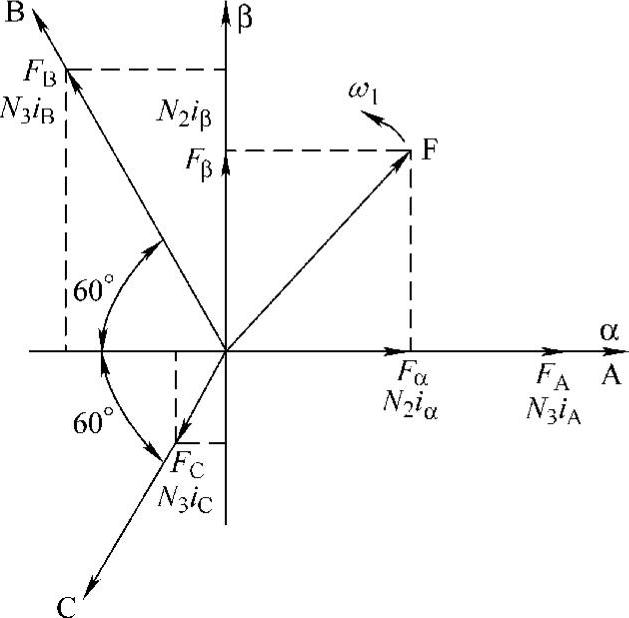
图4.2 3s/2s坐标系变换
在二相对称绕组中通以二相对称电流,在二相坐标系αβ的轴线上产生二相磁动势Fα、Fβ(见图4.2),Fα=N2iα、Fβ=N2iβ,式中N2为二相绕组匝数。Fα和Fβ的合成磁动势是旋转的。按磁动势等效原则,如果二相合成磁动势的大小和旋转速度与三相对称绕组产生的合成磁动势F相同,则三相绕组和二相绕组可以互相等效。一般将二相坐标系的α轴放在三相坐标系的A轴上,如图4.2所示,将三相磁动势FA、FB、FC投影到二相坐标系的α和β轴上,可以建立二相绕组与三相绕组的磁动势等效关系
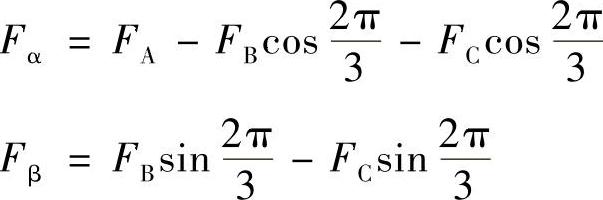
即

以矩阵形式表示为

并且二相/三相的变换关系为
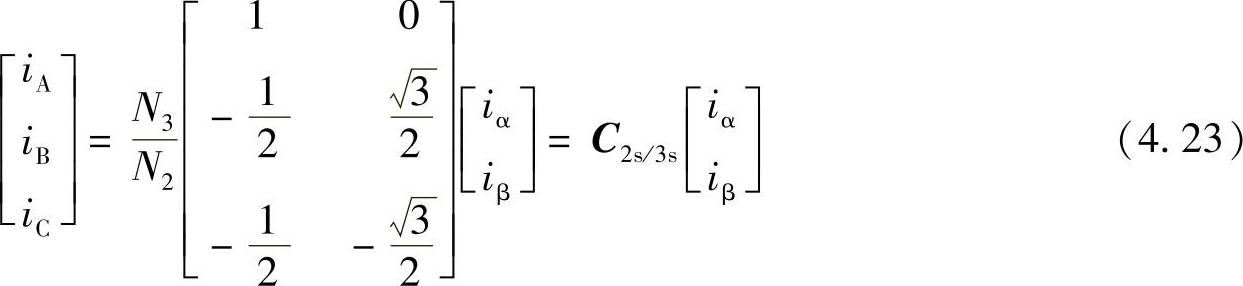
式中
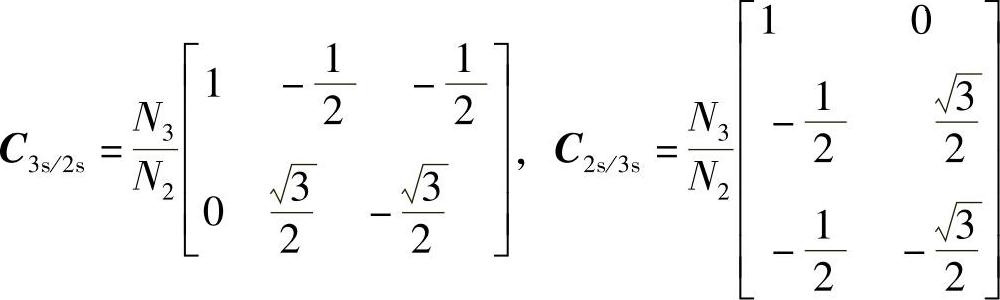
可以证明,C3s/2s、C2s/3s既是电流的变换矩阵,也是电压和磁链的变换矩阵。
将式(4.19)的三相电流代入式(4.22),在三相平衡时,iA+iB+iC=0,可得
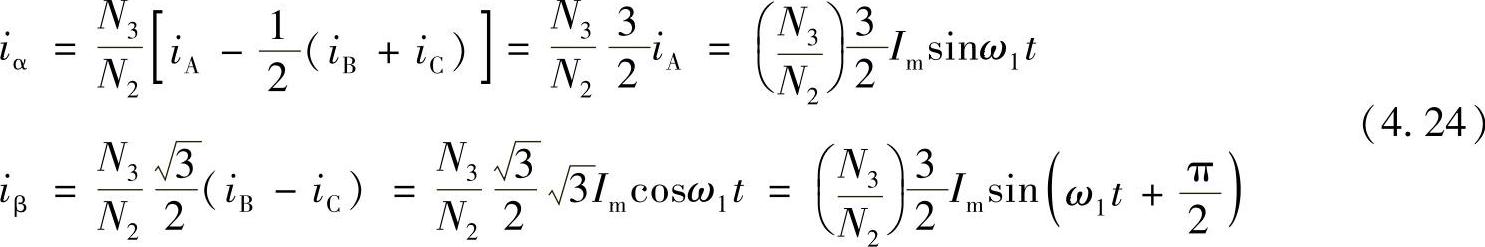
式(4.24)表明,按磁动势相等原则,经三相到二相的变换后,二相静止坐标系上的电流iα、iβ的幅值是原三相电流的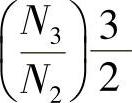 倍,其频率与三相电流频率相同,iα和iβ在相位上互差90°。如果要求保持变换前后三相绕组总功率与二相绕组的总功率也相等,可以证明,
倍,其频率与三相电流频率相同,iα和iβ在相位上互差90°。如果要求保持变换前后三相绕组总功率与二相绕组的总功率也相等,可以证明, ,因此三相绕组与二相绕组的匝数比为
,因此三相绕组与二相绕组的匝数比为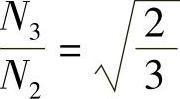 。由式(4.24)可以看到,二相绕组的电流较原来的三相电流要增加
。由式(4.24)可以看到,二相绕组的电流较原来的三相电流要增加 倍,每相电压和磁链也要增加
倍,每相电压和磁链也要增加 倍,二相绕组的一相功率是三相绕组一相功率的
倍,二相绕组的一相功率是三相绕组一相功率的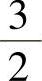 倍。如果保持变换前后的匝数相同,
倍。如果保持变换前后的匝数相同, ,则二相绕组每相的电流、电压和磁链较三相时要增加
,则二相绕组每相的电流、电压和磁链较三相时要增加 倍。如果保持变换后的电流幅值相同,则有
倍。如果保持变换后的电流幅值相同,则有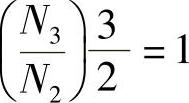 ,
,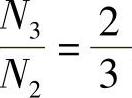 。从式(4.24)还可以看到,在二相静止坐标系上,二相电流iα、iβ的相位差为
。从式(4.24)还可以看到,在二相静止坐标系上,二相电流iα、iβ的相位差为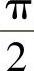 。
。

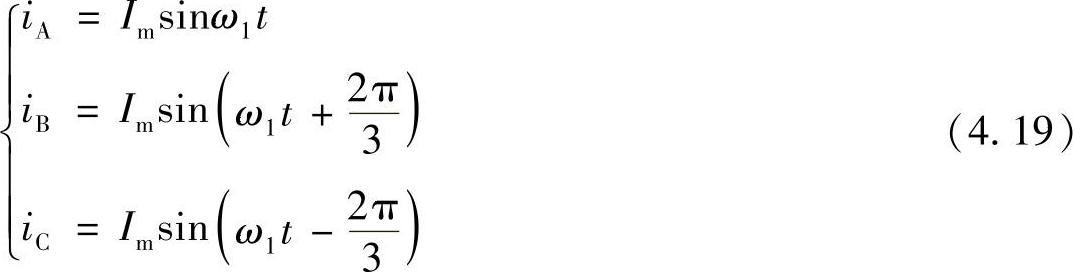


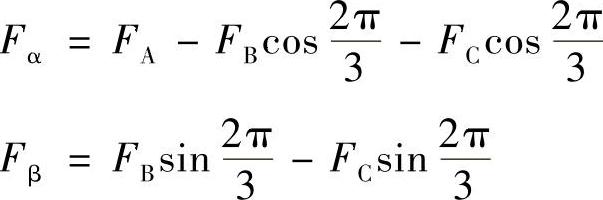


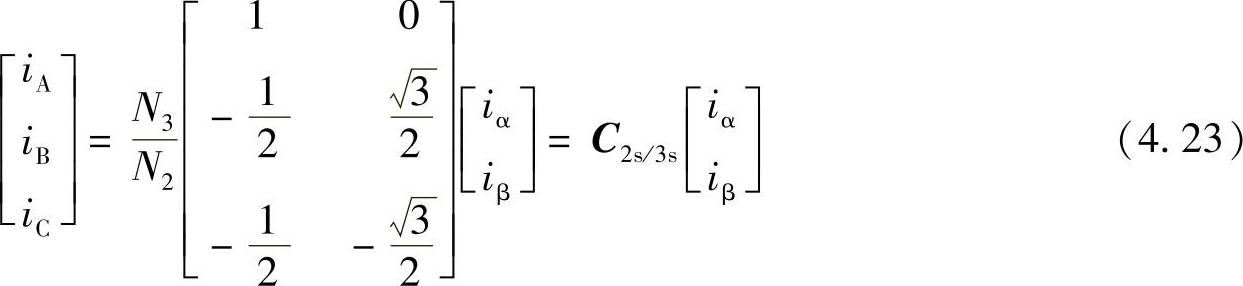
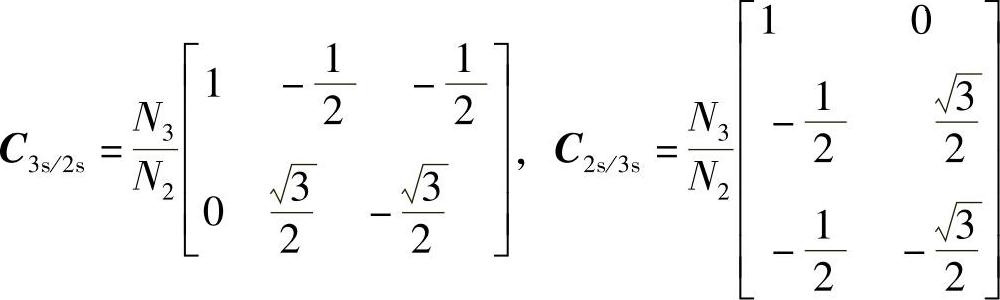
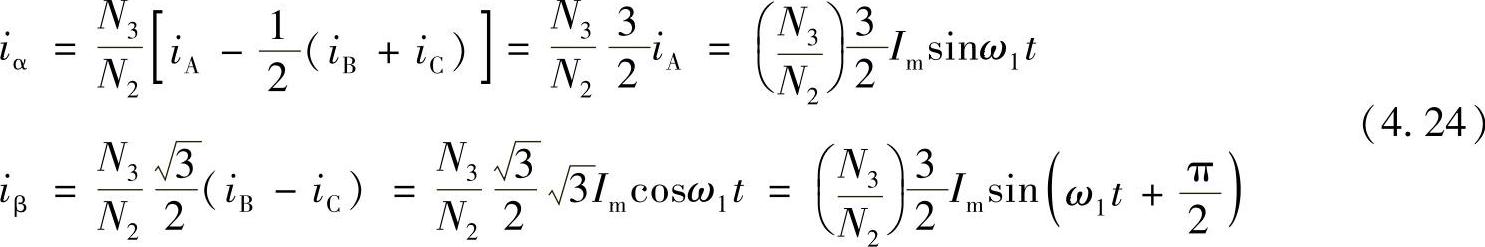
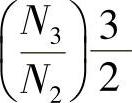 倍,其频率与三相电流频率相同,
倍,其频率与三相电流频率相同, ,因此三相绕组与二相绕组的匝数比为
,因此三相绕组与二相绕组的匝数比为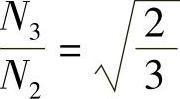 。由式(4.24)可以看到,二相绕组的电流较原来的三相电流要增加
。由式(4.24)可以看到,二相绕组的电流较原来的三相电流要增加 倍,每
倍,每 倍,二相绕组的一相功率是三相绕组一相功率的
倍,二相绕组的一相功率是三相绕组一相功率的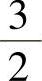 倍。如果保持变换前后的匝数相同,
倍。如果保持变换前后的匝数相同, ,则二相绕组每相的电流、电压和磁链较三相时要增加
,则二相绕组每相的电流、电压和磁链较三相时要增加 倍。如果保持变换后的电流幅值相同,则有
倍。如果保持变换后的电流幅值相同,则有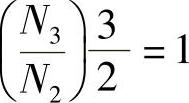 ,
,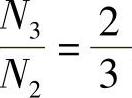 。从式(4.24)还可以看到,在二相静止坐标系上,二相电流
。从式(4.24)还可以看到,在二相静止坐标系上,二相电流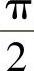 。
。





相关推荐