转差频率控制系统仿真，实现理想转速控制

2025-09-29 理论教育版权反馈

【摘要】：图3.29显示了定子磁链轨迹，磁链轨迹基本呈圆形，但是跟踪控制产生的电流毛刺使磁链轨迹不光滑。从磁链曲线比较恒压频比控制和转差频率控制的效果，差别是明显的，虽然二者都是按稳态模型控制，但转差频率控制在转速稳定后磁链的波动较小。

1.转差频率控制系统仿真模型

按转差频率控制系统原理（见图3.24）建立的仿真模型如图3.26所示。模型的主电路由逆变器和异步电动机模块连接组成，控制电路包括转速给定Constant模块和转速调节器PIASR模块等。函数发生器模块Is（Ws）按式（3.41）计算定子电流给定值I_s^∗，Fcn1～Fcn3模块按式（3.42）生成三相电流函数。三相滞环控制器模块Subsystem中包含六个滞环Relay控制模块（见图3.27），通过三相反馈电流与给定波形比较产生六路驱动脉冲。

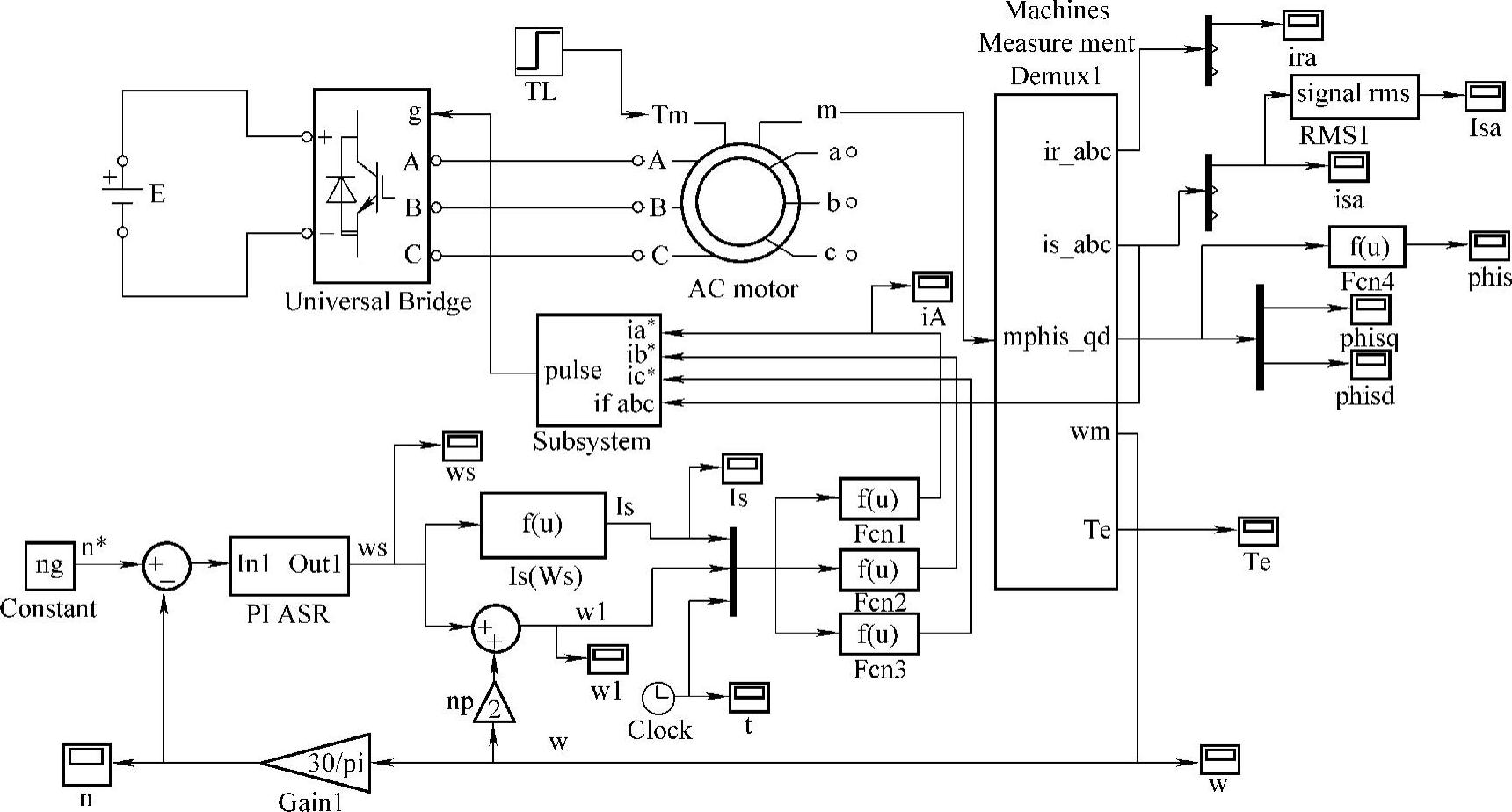
图3.26 转差频率控制系统仿真模型

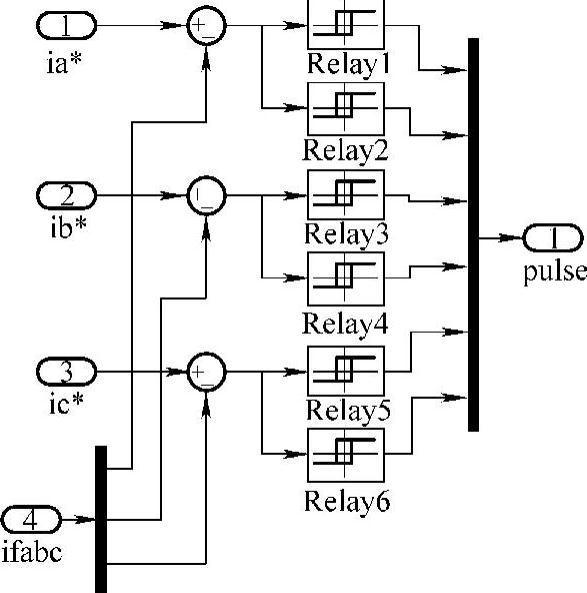
图3.27 三相滞环控制器

2.仿真分析

例3.2仿真异步电动机参数与例3.1相同，其他模块参数见表3.3，在转差频率控制中，确定励磁电流I_m很重要，I_m近似为电动机空载时的定子电流，或额定状态。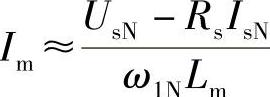

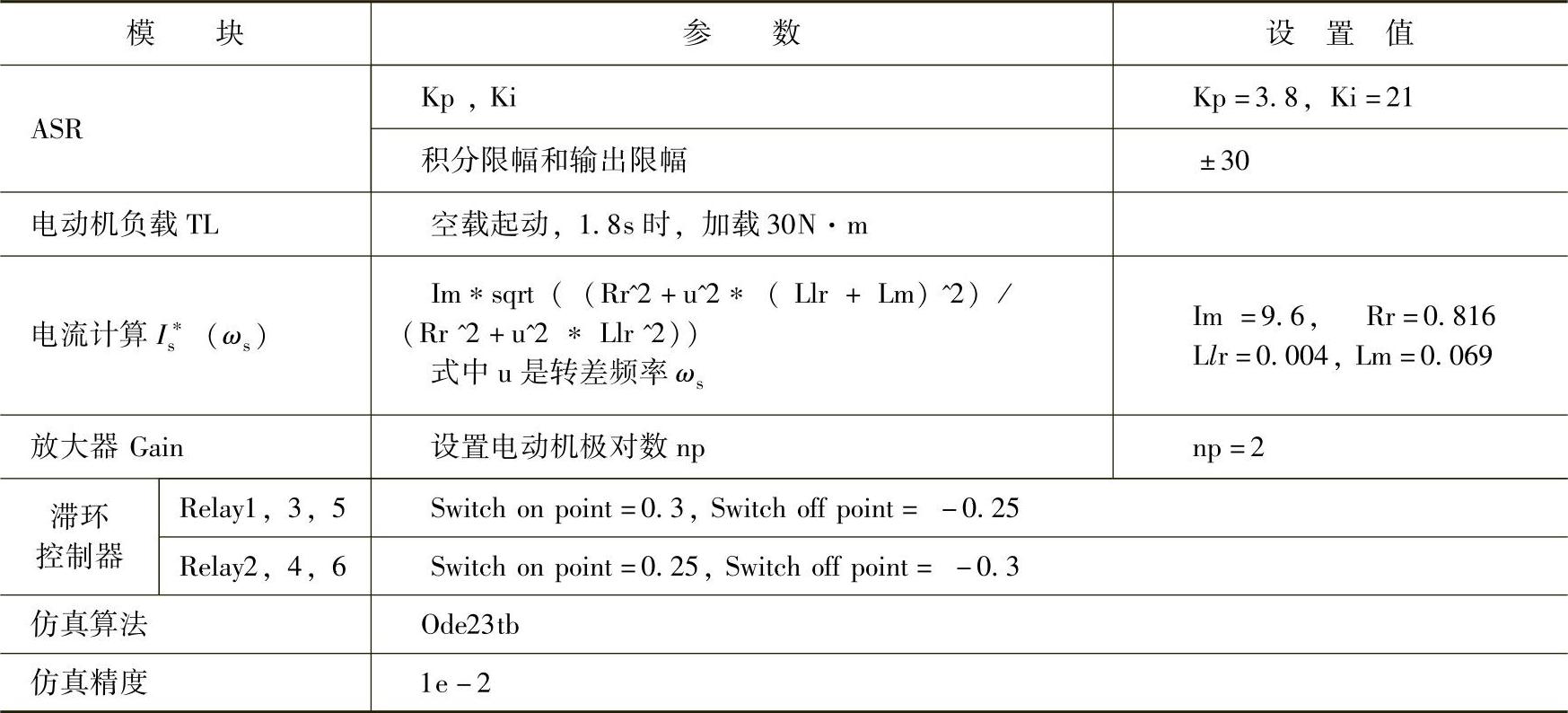
表3.3 转差频率控制模型的模块参数

(https://www.chuimin.cn)

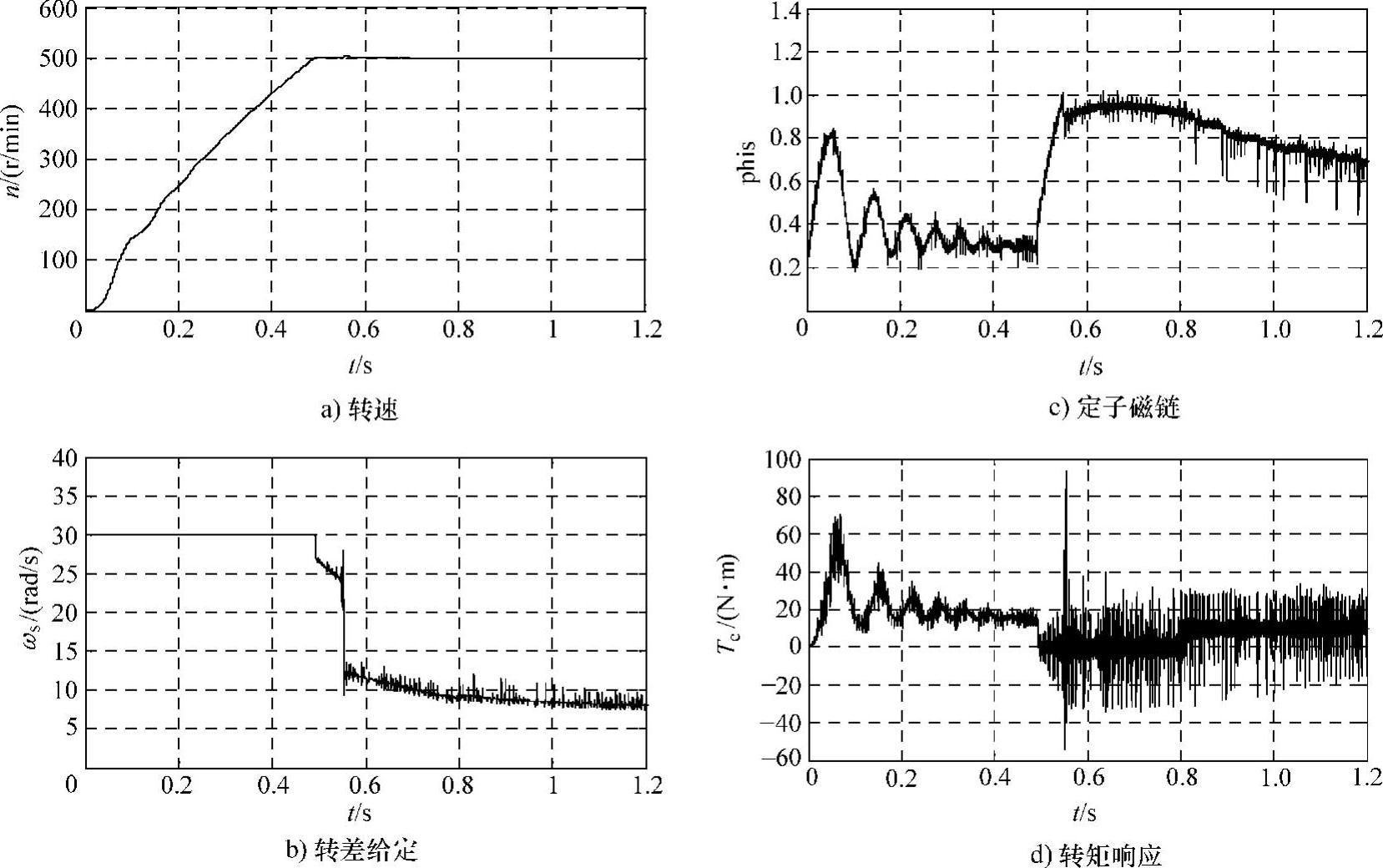
图3.28 给定500r/min时系统响应波形

在转速给定为500r/min时模型各响应波形如图3.28所示。图3.28a所示是系统的转速响应，0～0.5s是电动机起动阶段，转速基本没有超调，在0.8s时加载10N·m对转速的影响也不大。图3.28b所示是ASR输出的转差频率，起动中ASR饱和，输出为限幅值ω^∗_s_m=30，起动后ω_s^∗减小。图3.28e所示是根据ω_s^∗计算的定子电流I_s^∗，I_s^∗的变化与ω_s^∗曲线对应。图3.28c所示是仿真得到的定子磁链幅值，在起动时定子磁链有较大起伏，起动后磁链比较平稳，磁链的变化对电动机转矩（见图3.28d）和电流（见图3.28f）都有影响，从图3.28d可见0.8s加载时电动机转矩的反应，但电流的变化不明显，主要是因为加载较小，电流的转矩分量较小。图3.29显示了定子磁链轨迹，磁链轨迹基本呈圆形，但是跟踪控制产生的电流毛刺使磁链轨迹不光滑。图3.30所示的转矩-转速特性反映起动中，在转速到300r/min后基本是恒转矩起动，但是在500r/min左右转矩有较大波动。此波动与转矩曲线0.55s的波动对应（见图3.28d）。该模型的转速设定不能太大，较高转速设定在转速调节阶段易引起跳频现象，使电动机运行不稳定。模型ASR的输出限幅ω^∗_s_m对系统运行影响很大，当ω^∗_s_m限幅值较大时，电动机起动电流和转矩大，起动速度快，但定子电流频率的急剧变化也易引起跳频；当ω^∗_s_m限幅值较小时，起动时间长，起动较平稳，但较小的ω^∗_s_m限制了电动机的负载能力。因为模型的计算量大，仿真需要较长时间，所以本例仿真折中设置了ω^∗_s_m=±30。从磁链曲线比较恒压频比控制（见图3.20e）和转差频率控制（见图3.28c）的效果，差别是明显的，虽然二者都是按稳态模型控制，但转差频率控制在转速稳定后磁链的波动较小。

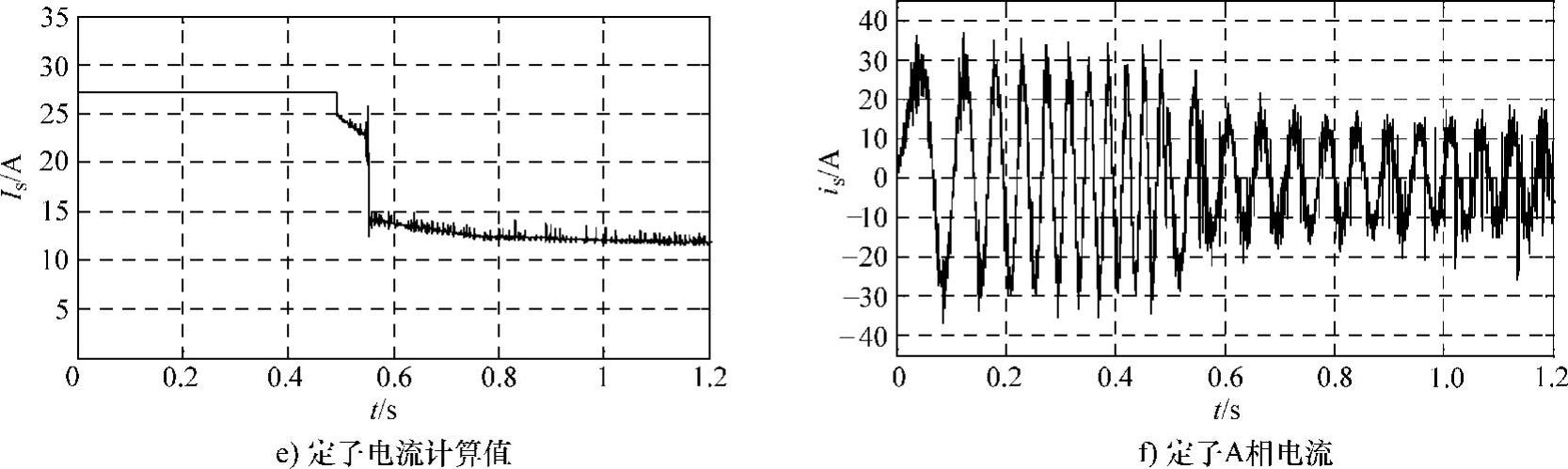
图3.28 给定500r/min时系统响应波形（续）

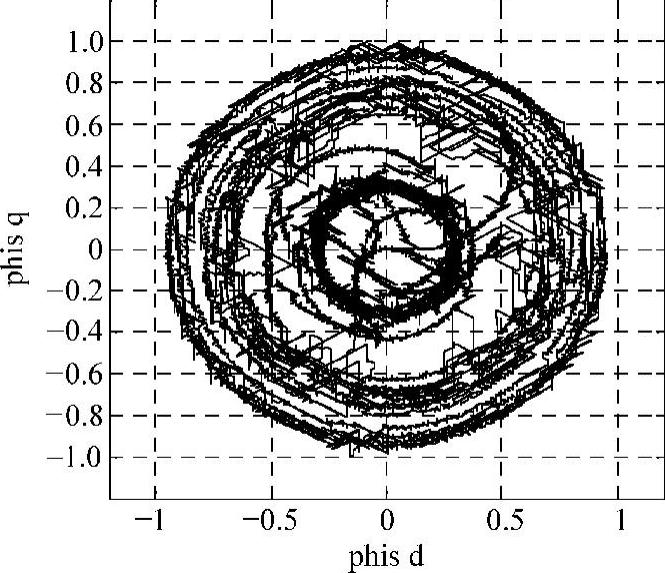
图3.29 定子磁链轨迹

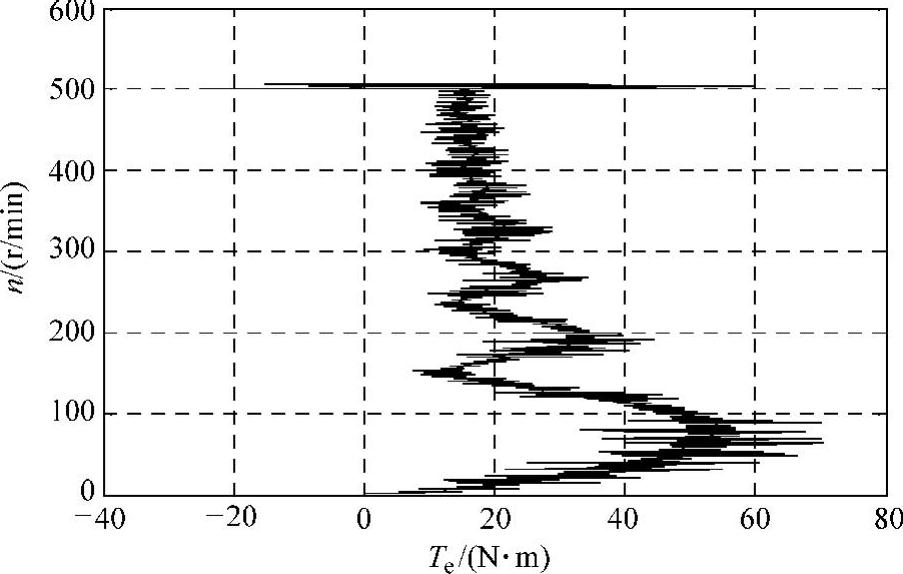
图3.30 转矩-转速特性

转差频率控制系统仿真，实现理想转速控制

相关推荐