简单的尼迈亚模型是一种经验公式类型的电弧数学模型，按图8-1所示，断路器开断过程可分成4个过程，它们是1）瞬动电磁铁动作过程；2）电弧停滞过程；3）电弧运动过程；4）电弧进入电弧栅片熄灭过程。经过停滞阶段后，电弧开始运动，迅速从动触头转移到导弧板，并在磁场力的作用下向栅片运动，计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型，这里介绍尼迈亚模型，它由L.Niemeyer博士于1984年提出[1]。......
2025-09-29
异步电动机稳态数学模型优化
【摘要】：图3.1a所示模型中转子和定子的频率不同，转子和定子回路之间由互感联系，不便于计算，一般通过频率折算、绕组折算和磁通折算得到异步电动机的等效模型，如图3.1b所示。电动机定子互感电动势Esm和转子互感电动势Erm的关系为Eg=Esm=keErm （3.6）其中式中，N1、N2分别为定子和转子一相绕组匝数；kW1、kW2分别为定子和转子的绕组系数。
三相电动机的稳态是指电动机负载、转速、电压和频率都稳定时的工作状态，这时电动机三相电压和电流对称，各相电压电流有效值相同，因此三相笼型异步电动机中的任意一相都可以用图3.1a所示的模型来表示。图中，Rs、Rr分别为定子和转子一相绕组的电阻，RL为负载折算的电阻，Lls、Llr分别为定子和转子一相绕组的漏感，Lm为定子和转子绕组间的互感，Esm为定子绕组的感应电动势，Erm为转子绕组的感应电动势。Esm和Erm的计算公式为
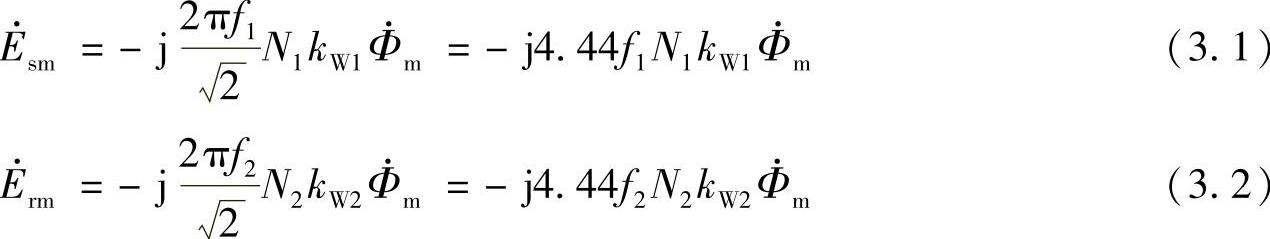
式中，f1和f2分别是定子和转子电流频率；Φm为一相气隙互感磁通。
图3.1a所示模型中转子和定子的频率不同，转子和定子回路之间由互感联系，不便于计算，一般通过频率折算、绕组折算和磁通折算得到异步电动机的等效模型，如图3.1b所示。经过折算的等效模型转子频率与定子频率相同，转子感应电动势与定子感应电动势相同，转子和定子回路可以连接在一起。折算可以将转子侧参数折算到定子侧，也可以将定子侧参数折算到转子侧，一般常用转子侧参数折算到定子侧，折算后转子频率f2为
f2=sf1 （3.3）
式中，s为稳态时转子转速的转差率
n0为同步转速（r/min）
图3.1 笼型异步电动机稳态模型
将转子频率折算为定子频率f1，实际上是将转子看成静止不转的，转子的旋转以转差率s表示。
电动机定子互感电动势Esm和转子互感电动势Erm的关系为(https://www.chuimin.cn)
Eg=Esm=keErm （3.6）其中
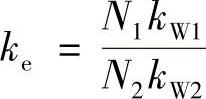
式中，N1、N2分别为定子和转子一相绕组匝数；kW1、kW2分别为定子和转子的绕组系数。
转子折算电流I′r为
如果定子和转子相数相同，即m1=m2（笼型异步电动机转子相数为转子导条数，一般需要先折算为定子相数），则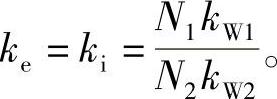
折算后转子电阻R′r和转子漏抗Ll′r为
R′r=kekiRr （3.8）
L′lr=kekiLlr （3.9）
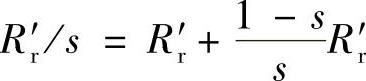
式中，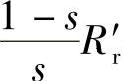
为负载折算的电阻。
相关文章
- 详细阅读
-
交流异步电动机的使用及优化详细阅读
额定运行时，转差率一般在0.01～0.06，即电动机的转速接近同步转速的。从原理上看，三相交流异步电动机调速的办法可以有三种途径：改变输入频率f；改变转差率s；改变磁极对数p。而改变三相交流异步电动机的转向仅需要改变三相中的任意两相即可。......
2025-09-29
-
双闭环控制直流调速系统的稳态参数和特性优化详细阅读
图1.35 转速电流闭环控制系统静特性3.转速和电流反馈系数的整定双闭环调速系统转速和电流反馈系数是系统调试时必须要整定的两个参数。......
2025-09-29
-
相异步电动机调速控制电路优化方案详细阅读
各种机床设备对三相异步电动机拖动的要求是，不仅能实现起动、停止、制动等操作，而且还要其能进行调速。所谓调速，是指用人为的方法，在负载转矩不变的情况下，通过改变三相异步电动机的参数或改变机械变速箱的变速比而得到不同的转速，以满足各种机床设备和机械加工工艺对不同转速的要求。......
2025-09-29
-
三相异步电动机机械制动控制电路优化方案详细阅读
三相异步电动机的机械制动，是在其切断三相交流电源后，利用机械装置强迫其立即停转。闸轮通过其轴与三相异步电动机的轴连接在一起，同步运行。当重物吊到一定高度时，若控制电路突然发生故障，使三相异步电动机断电停转，电磁制动器线圈也断电，闸瓦立即抱住闸轮使三相异步电动机迅速制动停转，从而可防止重物掉下造成事故。......
2025-09-29
-
三相异步电动机软起动控制电路优化方案详细阅读
当三相异步电动机起动完成后，接触器KM1的主触头闭合，由其为三相异步电动机提供电流而正常运行。软起动器不仅能用于三相异步电动机的起动控制，也可用于三相异步电动机的软停止控制，以减少停机过程中所产生的振动。因此，对三相异步电动机和机械传动装置等的损害减到最小程度。......
2025-09-29
-
三相异步电动机电气制动控制电路优化方案详细阅读
三相异步电动机电气制动控制是指在其断电停转的过程中，通过三相电源相序的转换或改变其供电条件，使其产生与原旋转方向相反的电磁转矩即制动转矩，将三相异步电动机立即停转或限制其转速的方法。主电路中串入三只电阻，用于限制在反接制动过程中产生的大电流，避免其对三相异步电动机定子绕组的损害。当三相异步电动机正、反转运行需要双向能耗制动时，见图2-20。......
2025-09-29
-
三相异步电动机正反转手动控制电路优化详细阅读
在一些较简单的机床设备中，如小台钻等，都还是采用手动方式来控制三相异步电动机的正、反转，实现加工过程中两个方向的交替运行。其工作原理就是利用动触头的转动来使六个静触头分三组接通或分断，实现对三相异步电动机改变旋转方向的控制。当手柄处于“停止”挡位时，两组动触头与三对静触头分断，三相异步电动机因未接入三相电源而不能转动及停转。......
2025-09-29
相关推荐