双闭环控制直流调速系统的调节器设计,一般都遵循先内环、后外环的原则,即先设计好电流环,然后设计转速环。图1.39 转速电流双闭环控制直流调速系统动态结构图1.电流调节器设计电流环的简化 电流环结构图如图1.40a所示。以上双闭环控制直流调速系统工程设计方法,主要是从系统的跟随性能出发,没有讨论系统的抗扰性能。产生这个问题的原因是表1.7的超调量都是按调节器在线性状态计算的,而实际系统调节器输出有限幅。......
2023-06-19
双闭环控制直流调速系统的转速调节器和电流调节器的设计基础是自动控制理论。自动控制理论介绍了多种基于时域和频域的设计方法,这些方法都是在原始系统的基础上,通过调节器校正使系统获得更好的稳态和动态性能的,设计中调节器参数一般都需要经过反复试凑,比较复杂、较难掌握,在工程上使用也很不方便。因此,工程设计需要简明实用的方法。对数频率特性[伯德图]是常用的调节器校正方法,它可以通过系统开环对数频率特性判定闭环系统的稳定性和稳定裕度,大致确定系统的稳态和动态性能。但是在伯德图上设计和校正系统也需要相当的经验和技巧,以往画伯德图需要在对数坐标纸上,尽管现在画伯德图有了计算机工具,但没有一定经验仍难以胜任。下面介绍的调节器工程设计方法,思路清晰,公式简明易于记忆,已经在工程设计中广泛采用。
该调节器工程设计的基本思路是:深入研究两种最基本的系统(称为典型Ⅰ型系统和典型Ⅱ型系统),找到系统参数与系统响应之间的对应关系,若已知系统参数就可知道系统的响应,反之如果期望系统有什么响应,就能得到系统相应的参数;将典型系统的传递函数与要设计的原系统比较,就可以找到系统校正的方法。
该调节器工程设计的步骤是:
1)简化原系统传递函数,突出关键环节和重点参数的影响。
2)根据生产工艺的要求确定系统校正的目标,是校正为典型Ⅰ型系统还是典型Ⅱ型系统。一般典型Ⅰ型系统超调量较小,调节时间较长;典型Ⅱ型系统超调量较大,调节速度较快。
3)将简化后系统的传递函数与选择的典型系统传递函数比较,选择合适的调节器,并决定调节器参数,这样设计的系统就基本具有典型系统的响应特点。
1.典型系统
(1)典型Ⅰ型系统 典型Ⅰ型系统的结构图如图1.36a所示,系统具有单位反馈,其开环传递函数为
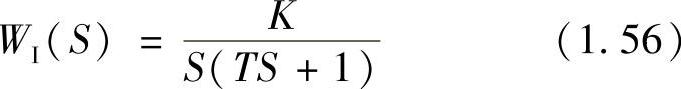
式中,K为系统的开环放大倍数;T为系统时间常数。
典型Ⅰ型系统只包含一个积分环节和一个惯性环节,惯性环节的时间常数T是系统自有的时间常数,它反映了系统的基本特征。典型Ⅰ型系统的开环对数频率特性如图1.36b所示,其幅频特性以-20dB/dec线穿越0dB/dec线,截止频率ωc和系统的相角稳定裕度γ见式(1.65)和式(1.66)。典型Ⅰ型系统只有一个可调参数,即放大倍数K。提高放大倍数K,则对数幅频频率特性向上移,系统的响应加快,但是系统的截止频率增加,系统的稳定裕度减小,如果放大倍数过大则系统则不易稳定。
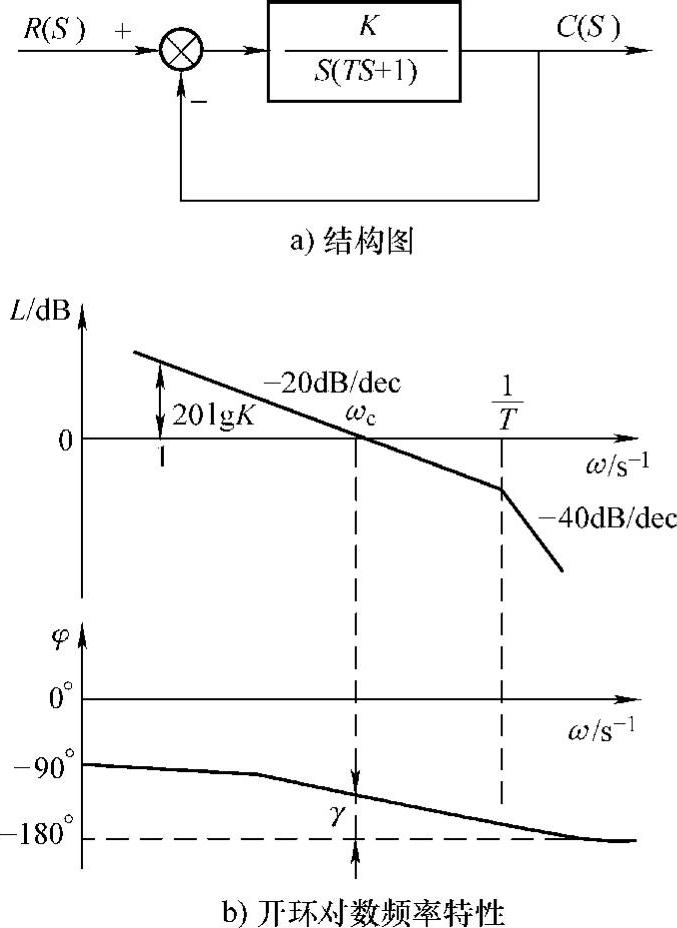
图1.36 典型Ⅰ型系统
典型Ⅰ型系统的闭环传递函数为

从闭环传递函数可以看到,这是一个二阶系统,对于二阶系统“自动控制原理”课程中已有详尽的分析,二阶系统的响应(超调量、上升时间等)与系统参数有明确的解析关系。
对比二阶系统的标准形式

闭环系统参数K、T与标准二阶系统参数ζ(阻尼系数)、ωn(谐振频率)之间关系为

在二阶系统中,ζ<1时系统动态响应为欠阻尼的振荡状态;ζ>1时系统响应呈过阻尼的单调上升状态,动态响应较慢;ζ=1时是临界阻尼状态。一般二阶系统都设计成欠阻尼状态,这样系统虽有一定的超调,但是响应速度较快。在欠阻尼状态,系统参数与系统响应之间关系为如下:
超调量

上升时间
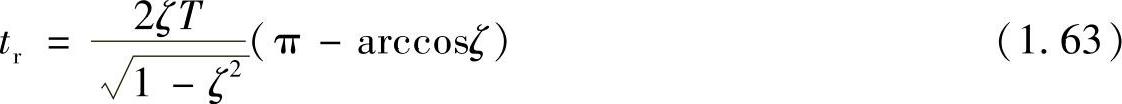
峰值时间

截止频率
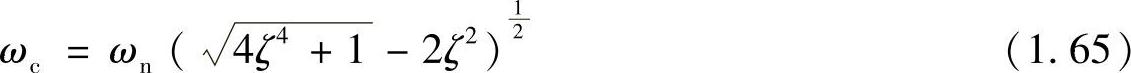
相角稳定裕度

根据以上系统响应关系以及典型Ⅰ型系统参数K、T与二阶系统参数ζ、ωn的关系,可以得到典型Ⅰ型系统参数与系统响应的关系,见表1.5。
表1.5 典型Ⅰ型系统参数与系统响应的关系

在调节器参数设计时,可以根据系统的动态要求,对σ、tp、tr、γ等指标进行综合考量,然后在表1.5中选择适合的典型Ⅰ型系统KT值。对选定的KT值,其中T是系统原有的时间常数,典型Ⅰ型系统的放大倍数K可以根据选定的KT值计算。
(2)典型Ⅱ型系统 典型Ⅱ型系统的闭环结构图如图1.37a所示,其开环传递函数为

开环传递函数包含了两个积分环节,一个惯性环节和一个微分环节,其中惯性环节的时间常数T是系统自有的时间常数,放大倍数K和微分时间常数τ是需要配置的。典型Ⅱ型系统的开环对数频率特性如图1.37b所示,典型Ⅱ型系统的两个积分环节和惯性环节的相位移已经超过180°,因此必须在分子上配置一个微分环节进行校正,将相频特性抬高,使系统有一定的稳定裕度。典型Ⅱ型系统是一个三阶系统,难于直接得到系统响应的数学表达式,这是三阶以上系统研究的难点。典型Ⅱ型系统的中频段宽度h对系统的影响很大,中频段越宽,系统的稳定性越好,系统输出对输入的跟随性能也就越好。中频段宽度的定义是
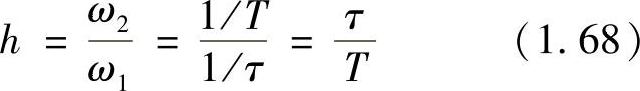
关于三阶系统参数的研究很多,这里重点介绍依据闭环系统“闭环幅频特性峰值Mr最小准则”的设计方法,该方法已得到工程界的广泛认同,因此也被称为三阶系统的工程设计方法。
闭环系统幅频特性峰值Mr表征了系统的超调量,按照Mrmin设计时,系统的最佳频比是
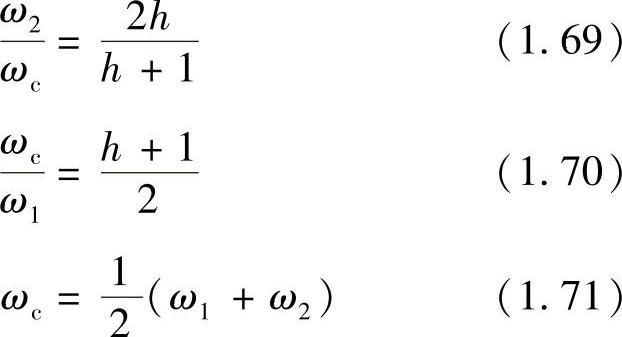
最佳频比时的最小闭环幅频特性的峰值为
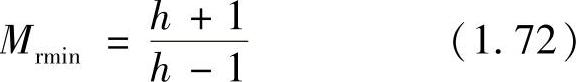
按照式(1.69)~式(1.72)计算的在不同h值时的Mrmin和对应的最佳频比见表1.6。

图1.37 典型Ⅱ型系统
表1.6 不同h值时的Mrmin和对应的最佳频比

在确定了系统的h和ωc之后,即可以计算系统开环传递函数的参数τ和K,有
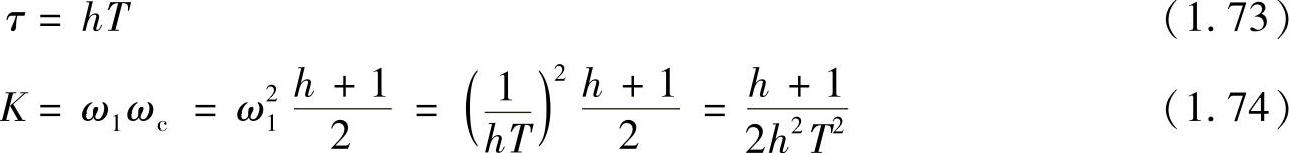
按“闭环幅频特性峰值Mr最小准则”设计典型Ⅱ型系统的关键是确定开环对数频率特性的中频段宽度h,h一旦确定,则开环传递函数的另一个参数开环放大倍数K就可以按式(1.74)确定,这是比较简便的参数设计方法,适合于工程应用。为了方便工程设计时确定中频段宽度,表1.7列出了h与时域响应超调量、上升时间等的关系。
典型Ⅰ型系统和典型Ⅱ型系统是两个比较简单的系统,但很实用,按这两种系统进行校正和设计,一般都能得到较好的效果。无论采用何种方法设计和选择的调节器参数,都是系统调试的基础,实际调试的结果可能与计算值有不同,这是因为理论设计的模型是经过了简化的理想模型,与实际系统毕竟有一定差距。但是,理论分析与计算是重要的,它奠定了设计的理论基础,不仅计算的参数是系统调试的重要依据,而且参数与响应之间的关系也指示了系统调试和改进的方向。
表1.7 典型Ⅱ型系统h与时域响应超调量、上升时间等的关系(按Mrmin设计)

2.系统结构图的简化
一个实际的系统往往是由多个环节组成的复杂系统,它的开环传递函数一般可以表示为
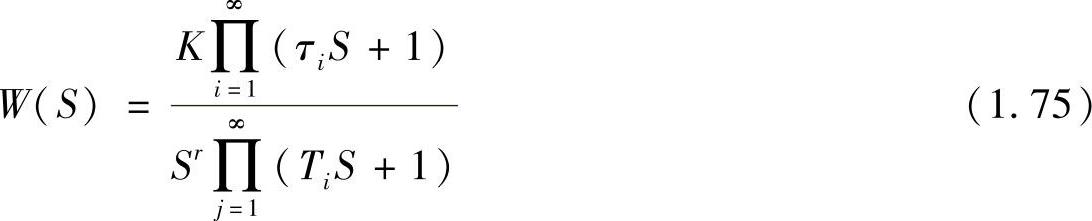
在环节较多时系统传递函数的阶数很高,在工程设计时需要简化,降低传递函数的阶数。虽然简化后的系统与原系统有一定差距,但是只要简化得合理就可以将差距控制在允许的范围内,不至产生较大的误差。常用的简化方法有高频段小惯性环节的近似处理、低频段大惯性环节的近似处理和高阶系统的降阶处理等。
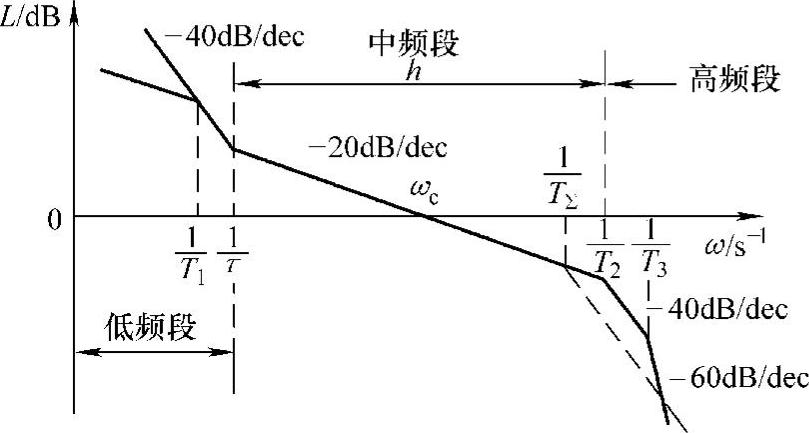
图1.38 传递函数的简化
1)高频段小惯性环节的近似处理。一般系统都包含一些时间常数较小的惯性环节,如滤波器时间常数、电力电子变流器的失控时间常数等,这些小时间常数都处在频率特性的高频段,如果这些小时间常数的交接频率离系统的截止频率ωc较远,则其对系统的影响就较小。若将这些高频段的小惯性环节用一个集中时间常数的小惯性环节来表示,则对系统性能的改变不大,但使系统得到了简化。如图1.38所示,系统开环传递函数高频段有T2、T3两个小惯性环节,这时可以用一个小惯性环节来近似表示
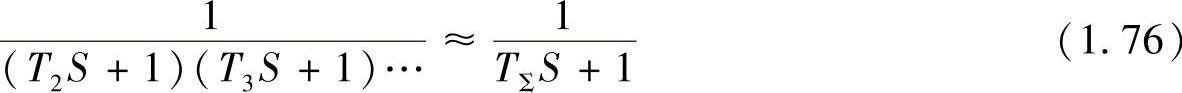
式中,TΣ=T2+T3。
近似的条件是,截止频率

如果高频段有三个小惯性环节,其时间常数分为T2、T3、T4,则

式中,TΣ=T2+T3+T4。近似的条件是
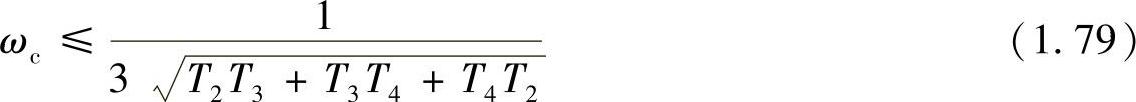
2)低频段大惯性环节的近似处理。如果系统开环传递函数存在一个时间常数特别大的惯性环节(低频段大惯性环节),如图1.38中的T1,则可以将它近似为一个积分环节

近似条件是

3)高阶系统的降阶处理。一般系统中经常有一些用二阶和三阶函数表示的控制环节,如电动机,这些环节在工程设计中较难处理,在一定条件下可以忽略其高次项,用一个一阶惯性环节来表示。例如:
二阶环节

近似条件是

三阶环节
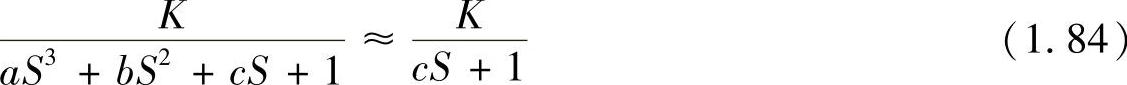
近似条件是

3.调节器选择和调节器参数
经过简化的系统还不是典型系统,需要用调节器将它校正为典型系统,采用的调节器要跟据简化后系统的传递函数而定。表1.8和表1.9给出了几种不同控制对象校正为典型Ⅰ型系统和典型Ⅱ型系统可以采用的调节器和参数配合。
表1.8 校正为典型Ⅰ型系统的调节器和参数配合

表1.9 校正为典型Ⅱ型系统的调节器和参数配合

有关电机运动控制系统的文章

双闭环控制直流调速系统的调节器设计,一般都遵循先内环、后外环的原则,即先设计好电流环,然后设计转速环。图1.39 转速电流双闭环控制直流调速系统动态结构图1.电流调节器设计电流环的简化 电流环结构图如图1.40a所示。以上双闭环控制直流调速系统工程设计方法,主要是从系统的跟随性能出发,没有讨论系统的抗扰性能。产生这个问题的原因是表1.7的超调量都是按调节器在线性状态计算的,而实际系统调节器输出有限幅。......
2023-06-19

下面以反馈控制理论为基础研究转速调节器的设计。有静差调速系统转速调节器的放大倍数 关于0型系统比例调节器放大倍数KP的设计在有静差调速系统分析时已经介绍,它可以根据满足调速指标时对转速闭环系统的转速降要求来确定。......
2023-06-19

将式转换为差分方程,得数字PI调节器的表达式,其第k拍输出为式中:Tsam为采样周期。数字PI调节器有位置式和增量式两种算法,式表述的差分方程为位置式算法,u为第k拍的输出值。位置式PI调节器的结构清晰,P和I两部分作用分明,参数调整简单明了。由式可知,PI调节器的第(k-1)拍输出为由式减去式,可得PI调节器输出增量增量式算法只需要当前的和上一拍的偏差即可计算输出值。......
2023-06-25

使用PLC构成控制系统,与同等规模的继电接触器系统相比,电气接线及开关接点已减少很多,故障也就大大降低。PLC的输入可直接与交流110V、直流24V等信号相连接,输出可直接驱动交流220V、直流24V的负载,无须再进行电平转换与光电隔离,因而可以方便地构成各种控制系统。......
2023-07-01

试设计一台无刷励磁发电机的手动励磁调节器。调压器TV的选择。强励时,流过调压器TV的最大电流即为变压器T的一次侧最大电流,即调压器最大容量应不小于:可选用容量为1.5kVA、电压为230/0~250V单相调压器。考虑1.6倍强励,流经每只二极管的最大电流为元件耐压不小于因此,可选用ZP100A/500V二极管。如果不考虑强励,则手动励磁调节器的变压器和调压器容量都可减少2.5倍,即600VA,考虑长期运行发热因素,可选用1kVA。......
2023-06-20

半闭环控制,减速器和丝杠间隙造成的误差在位置反馈环外,这些误差不能被抑制,因此控制准确度较全闭环控制低,但是成本低,安装和维护都比较方便。......
2023-06-19

测绘工程监理的设计阶段主要是业主或是委托技术设计单位或是测绘生产单位编制的技术设计能否满足工程总的控制目标,是否符合项目本身的技术标准和国家规范等。......
2023-06-28
相关推荐