首页 理论教育静差控制直流调速系统稳定性分析

静差控制直流调速系统稳定性分析

2023-06-19 理论教育 版权反馈
【摘要】：有静差调速系统由调节器、变流器、电动机和测速等环节组成，以传递函数表示各环节即组成系统的动态结构图，也称数学模型。由式，K=KPKsα/Ce，其中Ks、Ce在选定变流器和电动机后已经确定，α在选定给定Un和额定转速后也已经确定，对于有静差调速系统，唯一可调的只是放大器放大倍数KP，KP=KCe/αKs。

系统的稳定性和稳态特性的含义是不同的，稳定性是系统状态变化（给定和扰动）后，经过调整能否使输出重新稳定的能力，稳态特性是系统输出转速稳定后，转速与转矩或者说负载之间的关系。反馈控制系统的稳定性是系统能正常工作的前提条件，研究系统的稳定性，首先要建立系统的动态数学模型，然后根据稳定性判据判别系统的稳定性，在稳定性不足时采取一定的校正措施，使系统获得良好的动、静态性能。

有静差调速系统由调节器、变流器、电动机和测速等环节组成，以传递函数表示各环节即组成系统的动态结构图，也称数学模型。转速反馈有静差调速系统动态结构图如图1.17所示。

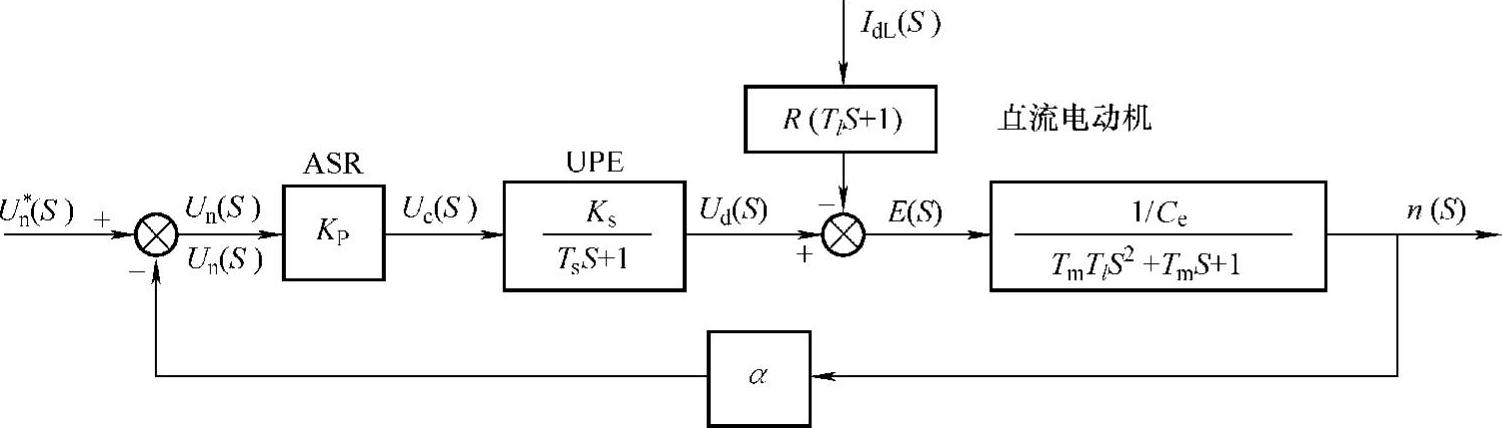
978-7-111-48427-1-Chapter01-66.jpg

图1.17 转速反馈有静差调速系统动态结构图

在系统动态结构图中，若将负载折算的电流IdL看成是一种扰动，在系统稳定性分析时暂不考虑，即令IdL=0，则从图1.17可以直接得到采用比例调节器的转速反馈调速系统的开环传递函数

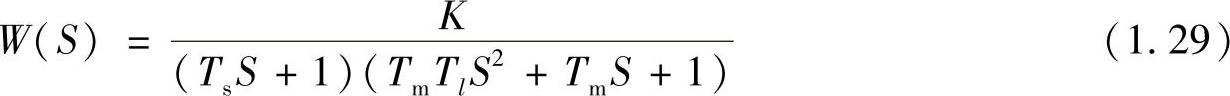
978-7-111-48427-1-Chapter01-67.jpg

式中，K为闭环系统的开环放大倍数

K=KPKsα/Ce （1.30）

从开环传递函数可以得到系统的闭环传递函数

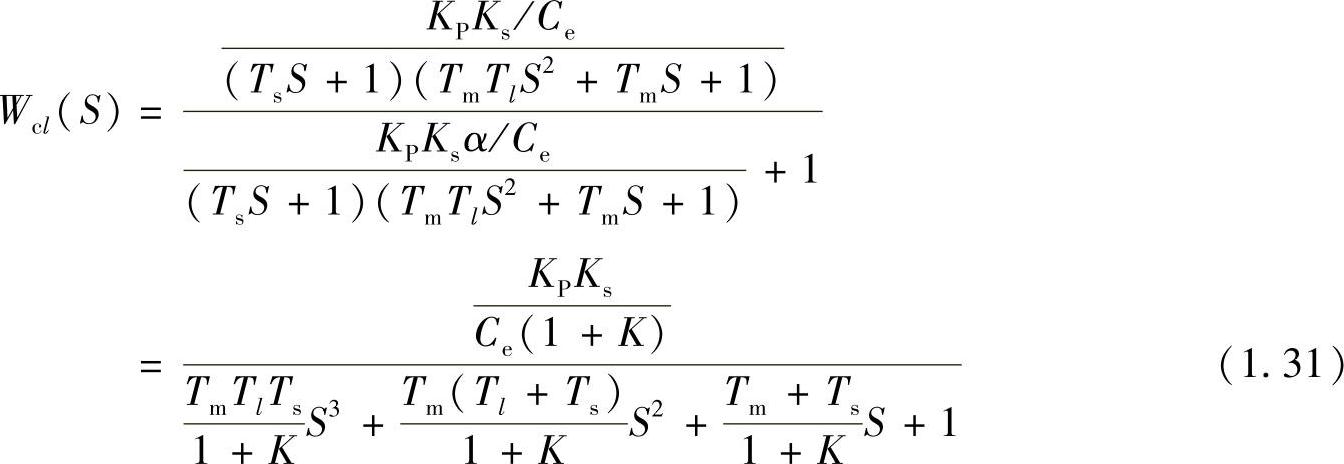
978-7-111-48427-1-Chapter01-68.jpg

系统闭环传递函数的特征方程为

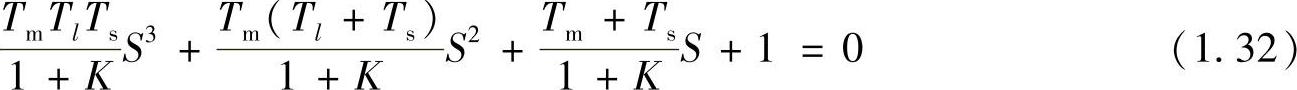
978-7-111-48427-1-Chapter01-69.jpg

在已知特征方程的基础上可以用代数判据（劳斯-赫尔维茨判据）得到系统的稳定条件。

三阶系统特征方程的标准形式为

a0S3+a1S2+a2S+a3=0稳定条件为a0>0，a1>0，a2>0，a3>0，a0>0，a1a2-a0a3>0

因为式（1.32）中各项系数都大于0，因此系统稳定还需要的条件是

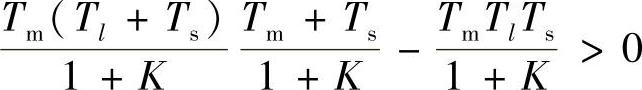
978-7-111-48427-1-Chapter01-70.jpg

整理得

978-7-111-48427-1-Chapter01-71.jpg

令

978-7-111-48427-1-Chapter01-72.jpg

Kcr称为系统的临界放大倍数，当系统的放大倍数K≥Kcr时系统将不稳定。因此系统设计时，既要使放大倍数K满足稳态指标（D，S）的要求，还要校核放大倍数K，看其是否满足系统稳定性的要求。由式（1.30），K=KPKsα/Ce，其中Ks、Ce在选定变流器和电动机后已经确定，α在选定给定Un∗和额定转速后也已经确定，对于有静差调速系统，唯一可调的只是放大器放大倍数KP，KP=KCe/αKs。当K能满足稳态指标（D，S），而不能满足系统稳定性的要求时，如果不能降低稳态指标，则需要考虑改变控制方案，例如采用无静差调速系统。

有关电机运动控制系统的文章

  • 静差控制直流调速系统动态性能分析 静差控制直流调速系统动态性能分析

    因此，采用比例调节器的系统是稳态转速有静差调速系统，静差是指稳态有偏差的系统。因此，转速反馈系数变化是系统不能克服的扰动，系统长期运行，振动和老化都可能引起测速发动机励磁或转速反馈电位器分压比的变化，使转速反馈系数发生变化，影响系统控制的精度。......

    2023-06-19

    详细阅读
  • 静差转速闭环控制直流调速系统稳态性能分析 静差转速闭环控制直流调速系统稳态性能分析

    在图1.12所示转速负反馈调速系统中，若转速调节器采用比例调节器则组成转速闭环控制的有静差直流调速系统。B点所对应的转速高于A′点，即闭环控制后，电动机由负载增加引起的转速降减小。因此，采用比例调节器的闭环控制系统必然是有静差调速系统，提高放大倍数KP可以减小偏差，但是不能消除偏差，而且放大倍数过大还会引起系统的不稳定。图1.14 开环和闭环控制静特性......

    2023-06-19

    详细阅读
  • 单闭环无静差调速系统的优化方案 单闭环无静差调速系统的优化方案

    在单闭环有静差调速系统中，由于采用比例调节器，稳态时转速只能接近给定值，而不可能完全等于给定值。图2-19输出限幅电路3.采用积分调节器和比例-积分调节器的单闭环无静差调速系统1）积分调节器构成的无静差系统有静差调速系统无法消除Δncl，当把比例调节器换成积分调节器后，这一情况马上得以改观。图2-24表示无静差系统的抗扰动过程。......

    2023-06-25

    详细阅读
  • 双闭环控制直流调速系统仿真优化 双闭环控制直流调速系统仿真优化

    表1.13 双闭环控制直流调速系统电流调节器参数和滤波器参数3.仿真与分析设置双闭环控制直流调速系统模型参数后，再设置仿真参数，仿真算法取ode15s，仿真时间预定为3s，启动仿真得到的转速和电枢电流波形如图1.56所示。......

    2023-06-19

    详细阅读
  • 微机双闭环直流调速控制系统 微机双闭环直流调速控制系统

    作为微机控制的全数字式双闭环直流电动机调速系统，其给定信号的输入是数据指令，通常由上位微型计算机通过串行或并行等通信方式来确定直流调速系统的速度和工作方式。微机控制的双闭环直流电动机调速系统的软件有主程序、初始化子程序和中断服务子程序等。......

    2023-06-25

    详细阅读
  • 带电流截止环节直流调速系统分析 带电流截止环节直流调速系统分析

    这些就是设计电流截止负反馈环节参数的依据。电流截止环节的参数能很容易根据其电路和截止电流Idcr值计算出来。......

    2023-06-25

    详细阅读
  • 直流调速系统弱磁控制的优化策略 直流调速系统弱磁控制的优化策略

    图2.28 调压调速和弱磁调速稳态参数关系虽然额定功率、额定电压和额定电流是电动机长期运行不能超过的，但是额定转速有一定的上调裕量，因此，采用弱磁升速可以扩大电动机的调速范围。即在调速范围要求较大的场合采取调压调速和弱磁调速相结合的方法，在额定转速以下采用调压调速，在额定转速以上采用弱磁调速，以扩大调速范围。......

    2023-06-19

    详细阅读
  • 自动弱磁控制直流调速系统优化方案 自动弱磁控制直流调速系统优化方案

    自动弱磁控制直流调速系统是基速以下采用调压调速，基速以上自动进行弱磁升速的调速系统，系统的组成如图2.29所示。图2.29 自动弱磁控制直流调速系统的组成系统弱磁控制过程如下：调节转速给定Un信号，转速上升，在转速没有达到额定转速时，因为电动势反馈信号Ue

    2023-06-19

    详细阅读