坐标变换与变换矩阵

2025-09-29 理论教育版权反馈

【摘要】：坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。

在得到异步电动机的动态数学模型后，要分析和求解这组非线性方程显然是十分困难的。在实际应用中必须设法予以简化，要简化数学模型，须从简化磁链关系入手，简化的基本方法是坐标变换。

坐标变换的思路是，将交流电动机的物理模型（见图2-2）等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。不同电动机模型彼此等效的原则是：在不同坐标下所产生的磁动势完全一致。

根据电机学知识，交流电动机三相对称的静止绕组A、B、C，通以三相平衡的正弦电流时，所产生的合成磁动势是旋转磁动势F，它在空间呈正弦分布，以同步转速ω₁（即电流的角频率）顺着A-B-C的相序旋转，如图2-2所示。

然而，旋转磁动势并不一定非要三相不可，除单相以外，二相、三相、四相等任意对称的多相绕组，通以平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。

图2-3中绘出了两相静止绕组α和β，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F。

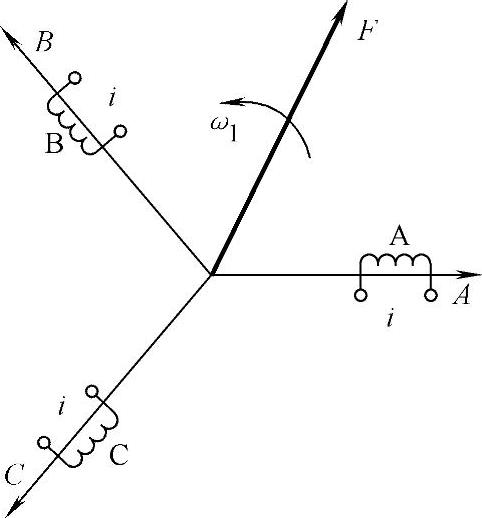
图2-2 三相交流绕组

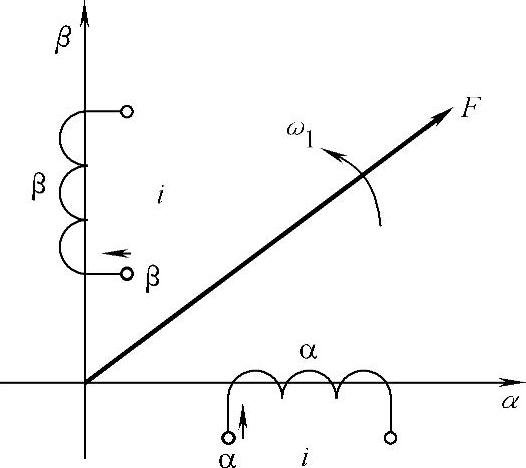
图2-3 两相交流绕组

当图2-2和图2-3中的两个旋转磁动势大小和转速都相等时，即认为图2-3的两相绕组与图2-2的三相绕组等效。

在图2-4中，两个匝数相等且互相垂直的绕组M和T，其中分别通以直流电流i_m和i_t，产生合成磁动势F，其位置相对于绕组来说是固定的。

让包含两个绕组在内的整个铁心以同步转速旋转，则磁动势F自然也随之旋转起来，成为旋转磁动势。如果这个旋转磁动势的大小和转速也控制成与图2-2和图2-3中的磁动势一样，那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。当观察者也站到铁心上绕组一起旋转时，M和T就是两个通以直流而相互垂直的静止绕组。

如果控制磁通的位置在M轴上，就和直流电动机物理模型没有本质上的区别了。这时，绕组M相当于励磁绕组，T相当于伪静止的电枢绕组。(https://www.chuimin.cn)

由此可见，以产生同样的旋转磁动势为准则，图2-2的三相交流绕组、图2-3的两相交流绕组和图2-4中整体旋转的直流绕组彼此等效。或者说，在三相坐标系下的i_A、i_B、i_C，在两相坐标系下的i_α、i_β和在旋转两相坐标系下的直流i_m、i_t是等效的，它们能产生相同的旋转磁动势。利用坐标变换就可以求出i_A、i_B、i_C与i_α、i_β和i_m、i_t之间准确的等效关系。

在三相静止绕组A、B、C和两相静止绕组α、β之间的变换，称三相静止坐标系和两相静止坐标系间的变换，简称3/2变换。为方便起见，取A轴和α轴重合。设三相绕组每相有效匝数为N₃，两相绕组每相有效匝数为N₂，各相磁动势为有效匝数与电流的乘积，其空间矢量均位于有关相的坐标轴上。考虑变换前后总功率不变，在此前提下，可以证明，匝数比应为N₃/N₂=2/3。i_A、i_B、i_C与i_α、i_β之间的等效关系如式（2-15）。从三相坐标系变换到两相坐标系的变换矩阵C₃/2，如式（2-16）。

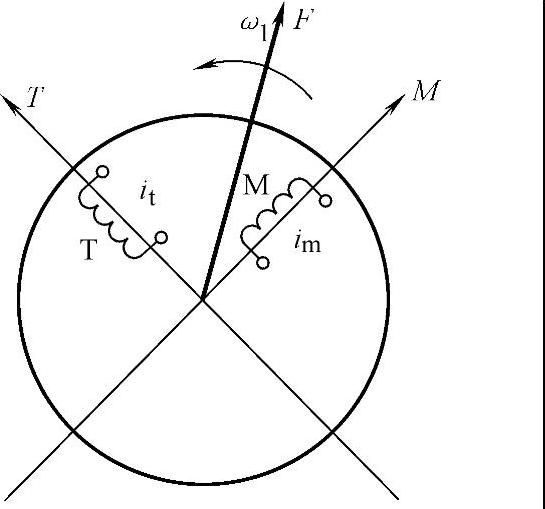
图2-4 旋转的直流绕组

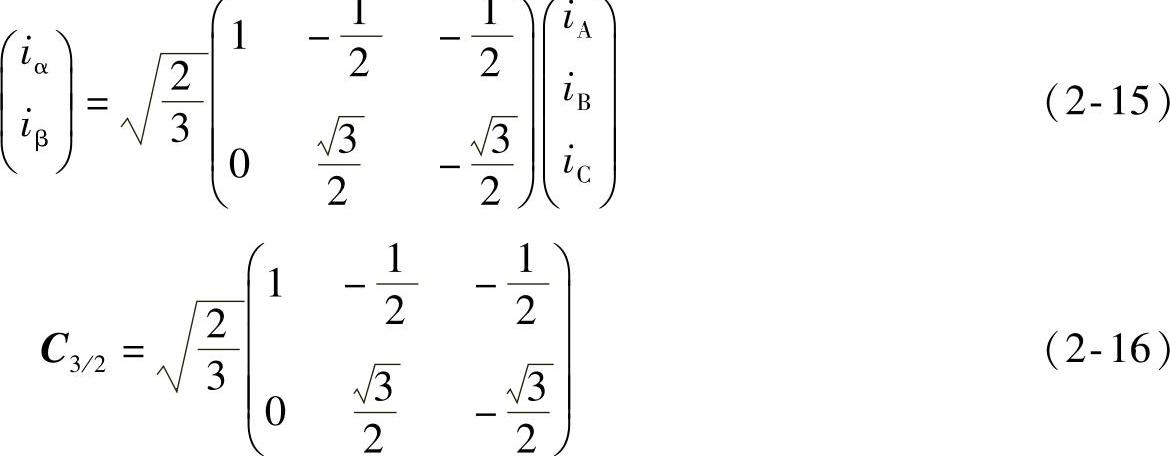
按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。

如果三相绕组是联结不带零线，则有i_A+i_B+i_C=0，或i_C=-i_A-i_B。代入式（2-15），并整理后得式（2-17）

在等效的交流电动机绕组和直流电动机绕组物理模型的图2-3和图2-4中，从两相静止坐标系到两相旋转坐标系M、T变换称作两相-两相旋转变换，简称2s/2r变换，其中s表示静止，r表示旋转。把两个坐标系画在一起，即得图2-5。图2-5中，两相交流电流i_α、i_β和两个直流电流i_m、i_t产生同样的以同步转速ω₁旋转的合成磁动势F_s。由于各绕组匝数都相等，可以消去磁动势中的匝数，直接用电流表示，例如F_s可以直接标成i_s。但必须注意，这里的电流都是空间矢量，而不是时间向量。

M、T轴和矢量F_s（is）都以转速ω₁旋转，分量i_m、i_t的长短不变，相当于M、T绕组的直流磁动势。由于α、β轴是静止的，α轴与M轴的夹角φ随时间而变化，因此i_s在α、β轴上的分量的长短也随时间变化，相当于绕组交流磁动势的瞬时值。由图可见i_α、i_β和i_m、i_t之间存在关系如式（2-18），C_2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。

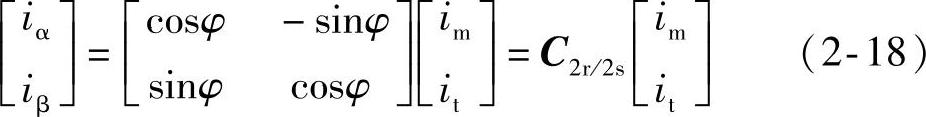
经过坐标变换简化了电动机的数学模型，把电动机变换到两相坐标系上，由于两相坐标轴互相垂直，两相绕组之间没有磁的耦合，使数学模型简单了许多。

坐标变换与变换矩阵

相关推荐