“数学建模”中“数学”是“建模”的限制词,因此需要先考察“建模”,“建模”中,动词“建”指建立、建构或者构造;名词“模”指模型,因此建模就是建立模型或者建构模型的意思.(一)模型《辞海》(2009)对“模型”一词有3项释义.(1)与“原型”相对研究对象的替代物原型,即客观存在的对象客体;模型是具有原型相似特征的替代物,是系统或过程的简化、抽象或类比表示.(2)根据实物、设计图或设想,按比例、形态或......
2023-08-17
为了分析和理解,进行如下假设:
1)忽略空间谐波,设三相绕组对称,在空间互差120°电角度,所产生的磁动势沿气隙周围按正弦规律分布;
2)忽略磁路饱和,各绕组的自感和互感都是恒定的;
3)忽略铁心损耗;
4)不考虑频率变化和温度变化对绕组电阻的影响。
无论电动机转子是绕线转子还是笼型转子,都将它等效成三相绕线转子,并将转子侧参数折算到定子侧,折算后的定子和转子绕组匝数都相等。这样,实际电动机绕组就等效成图2-1所示的三相异步电动机的物理模型。
图2-1中,定子三相绕组轴线A、B、C在空间是固定的,以A轴为参考坐标轴;转子绕组轴线a、b、c随转子旋转,转子a轴和定子A轴间的电角度θ为空间角位移变量。

图2-1 三相异步电动机的物理模型
规定各绕组电压、电流、磁链的正方向符合电动机惯例和右手螺旋法则。这时,异步电动机的数学模型由下述电压方程式、磁链方程式、转矩方程式和运动方程组成。式(2-1)为三相定子绕组的电压平衡方程,与此相应,式(2-2)为三相转子绕组折算到定子侧后的电压方程。
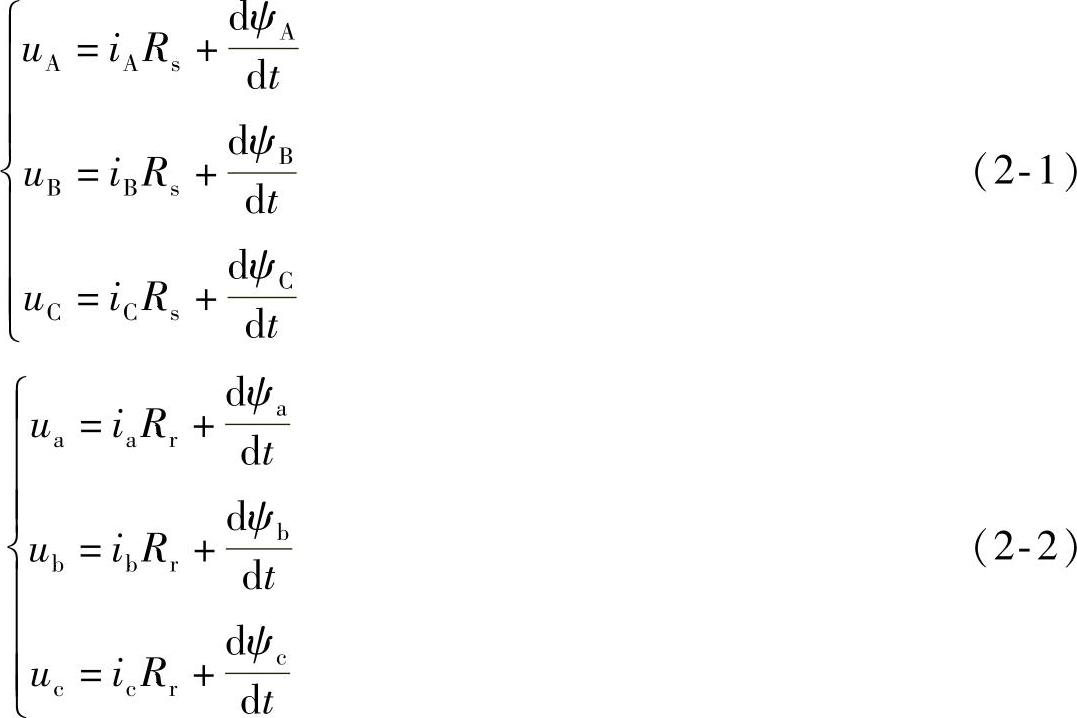
式中 uA、uB、uC、ua、ub和uc——定子和转子相电压的瞬时值;
iA、iB、iC、ia、ib、ic——定子和转子相电流的瞬时值;
ψA、ψB、ψC、ψa、ψb、ψc——各相绕组的磁链;
Rs、Rr——定子和转子绕组电阻。
上述转子各量都已折算到定子侧,为了简单起见,表示折算的上角标均省略,以下同此。
将电压方程写成矩阵形式,如式(2-3)所示,也可以写为式(2-4)的形式,并以微分算子p代替微分符号d/dt。

每个绕组的磁链是它本身的自感磁链和其他绕组对它的互感磁链之和,因此,6个绕组的磁链方程如式(2-5),也可以写为式(2-6)的形式。
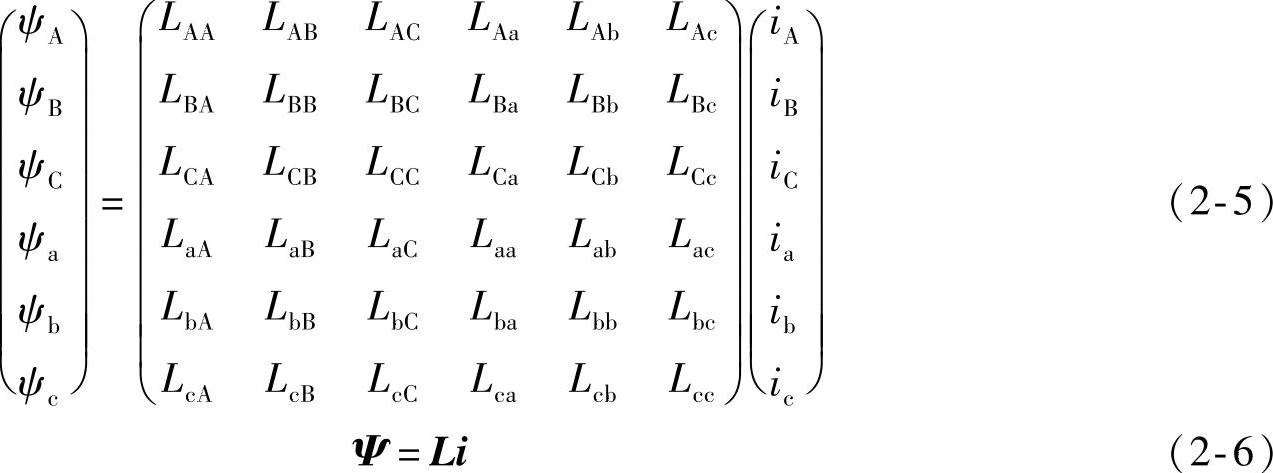
式中 L——6×6电感矩阵,其中对角线元素LAA、LBB、LCC、Laa、Lbb、Lcc是各有关定子或
转子绕组的自感,其余各项则是绕组间的互感。
实际上,与电动机绕组交链的磁通主要只有两类:一类是穿过气隙的相间互感磁通,即主磁通,另一类是只与一相绕组交链而不穿过气隙的漏磁通,前者是主要的。
对于每一相绕组来说,它所交链的磁通是互感磁通与漏感磁通之和,定子各相自感如式(2-7),转子各相自感如式(2-8)。
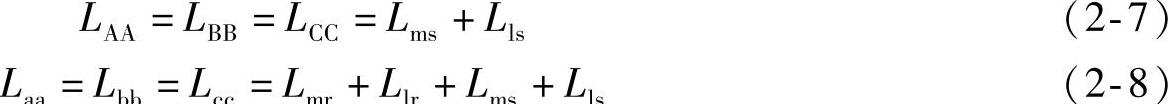
式中 Lls——定子各相漏磁通所对应的电感,由于绕组的对称性,各相漏感值均相等;
Llr——转子各相漏磁通所对应的电感;
Lms——与定子相绕组交链的最大互感;
Lmr——与转子相绕组交链的最大互感。
由于折算后定、转子绕组匝数相等,且各绕组间互感都通过气隙,磁阻相同,故可认为Lms=Lmr。
如果把磁链方程式(2-6)代入电压方程式(2-4)中,即得展开后的电压方程式(2-9)。

式中 θ——转子位置;
Ldi/dt——属于电磁感应电动势中的脉变电动势(或称变压器电动势);
(dL/dθ)ωi——属于电磁感应电动势中与转速成正比的旋转电动势。
根据机电能量转换原理,在多绕组电动机中,在线性电感的条件下,磁场的储能Wm和磁共能W′m表达式为式(2-10)。

而电磁转矩等于机械角位移变化时磁共能的变化率∂ (电流约束为常值),且机械角位移为θm=θ/np,np为磁极对数。于是电磁转矩Te表达式为式(2-11),将电感表达式代入,并且展开可以得到Te表达式为式(2-12),电磁转矩的正方向为使θ减小的方向。
(电流约束为常值),且机械角位移为θm=θ/np,np为磁极对数。于是电磁转矩Te表达式为式(2-11),将电感表达式代入,并且展开可以得到Te表达式为式(2-12),电磁转矩的正方向为使θ减小的方向。
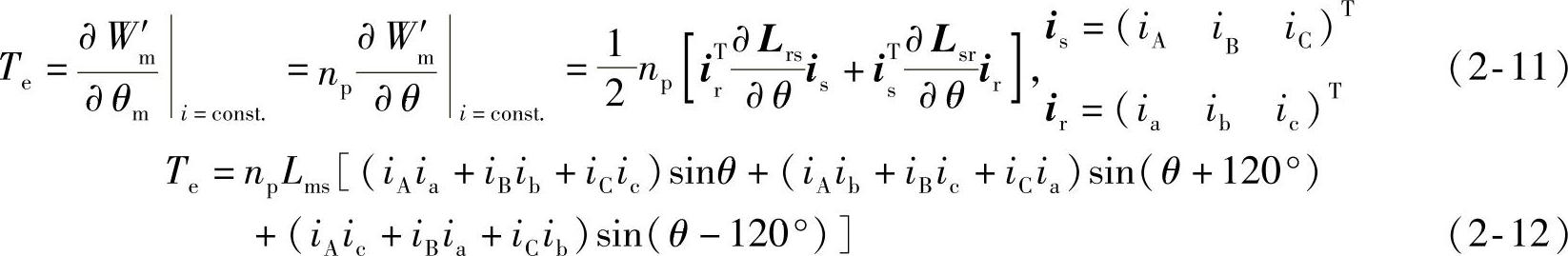
式(2-1)~式(2-12)是在线性磁路、磁动势在空间按正弦分布的假定条件下得出来的,但对定、转子电流对时间的波形未作任何假定,式中的i都是瞬时值。因此,上述电磁转矩公式完全适用于变压变频器供电的含有电流谐波的三相异步电机调速系统。
在一般情况下,电力拖动系统的运动方程式如式(2-13)。

式中 TL——负载阻转矩;
J——机组的转动惯量;
D——与转速成正比的阻转矩阻尼系数;
K——扭转弹性转矩系数。对于恒转矩负载,D=0,K=0,则Te表达式为式(2-14),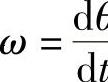 。
。

有关西门子系列变频器及其工程应用的文章

“数学建模”中“数学”是“建模”的限制词,因此需要先考察“建模”,“建模”中,动词“建”指建立、建构或者构造;名词“模”指模型,因此建模就是建立模型或者建构模型的意思.(一)模型《辞海》(2009)对“模型”一词有3项释义.(1)与“原型”相对研究对象的替代物原型,即客观存在的对象客体;模型是具有原型相似特征的替代物,是系统或过程的简化、抽象或类比表示.(2)根据实物、设计图或设想,按比例、形态或......
2023-08-17

如开设讲座、采集数学建模问题、研究建模方案、撰写建模小论文等,有些建模问题比较复杂,可以将其分解、分步解决,或在教师带领下解决某些环节,其具体求解过程可留给学生课后解决,最后再组织学生宣讲、交流或写成小论文,这种“零存整取”的做法,既发挥了教师的主导作用,体现了以学生为主体的原则,又培养了学生的探索精神和数学能力。......
2023-08-13

基于数学核心素养的教学就是要培养学生用数学的眼光看世界,因此,数学教师首先要能够用数学的眼光看世界,用数学的眼光看身边的事物,并在平时教学中能够注重基于教学内容的实际背景向学生渗透数学与实际生活的联系.(一)数学建模的教学原则数学建模活动作为《普通高中数学课程标准(2017年版)》课程内容之一,要求以课题形式,小组合作方式开展教学,最终以研究报告或小论文等多种形式呈现.数学建模活动的主要特征体现在......
2023-08-17

数学模型是用数学符号、函数关系将评价目标和内容系统规定下来,并把互相间的变化关系通过数学公式表达出来,这一过程就是数学建模的过程.数学建模作为问题解决的一种模式,体现了一个学生对原始问题的分析、假设和抽象的数学加工过程,是学生归纳理解以及创新能力的综合表现.数学模型教学能够能动地让学生用所学的数学必备知识去解决问题,能够培养学生对所学知识的“想用、能用、会用”的数学意识.试题中数学建模思想的意蕴解......
2023-08-17

苏联教育家马卡连柯曾说过:“游戏在儿童生活中具有重要的意义,具有与成人活动、工作和劳动同样重要的意义.”游戏本身具有愉快、自由及探索的特性,游戏是孩子们的天性,也是认识世界的途径之一,其不但可以满足学生的好奇心理,还能有效培养他们各方面的能力.如今数学建模的教学课堂普遍枯燥乏味,而简单的数学游戏能够通过创设一个游戏化的场景让学生更加放松,从而让学生对于传统教学模式不那么排斥,可以更有效地理解数学概......
2023-08-17

图3.1a所示模型中转子和定子的频率不同,转子和定子回路之间由互感联系,不便于计算,一般通过频率折算、绕组折算和磁通折算得到异步电动机的等效模型,如图3.1b所示。电动机定子互感电动势Esm和转子互感电动势Erm的关系为Eg=Esm=keErm (3.6)其中式中,N1、N2分别为定子和转子一相绕组匝数;kW1、kW2分别为定子和转子的绕组系数。......
2023-06-19

数学建模就是要培养学生用事物相互联系和发展变化的观点来分析问题,从而认识事物之间是相互联系和有规律地变化着的.数学建模是数学与其他领域之间建立联系的方法.数学建模的过程就是提出一个问题,然后细化问题,最后以精确的数学术语表述.一旦问题变成数学问题,就要使用数学来找到答案,并且最后必须逆转这一过程(这是很多人忘记的部分),将数学解转换回对原始问题的可理解的,有意义的答案.从思想上来说,数学建模是构建......
2023-08-17

“数学建模是运用数学思想、方法和知识解决实际问题的过程,已经成为不同层次数学教育重要和基本的内容”,数学建模就是用数学语言描述实际现象的过程。(三)数学建模的一般步骤例1哥尼斯堡七桥问题。建立模型分析:根据题意,设y表示旅馆一天的总收入,x为与160元相比降低的房价。事实上二次函数在[0,90]之内只有一个极值点25。......
2023-08-13
相关推荐