首页理论教育流动液体动量方程式优化方案

流动液体动量方程式优化方案

2023-06-18 理论教育版权反馈

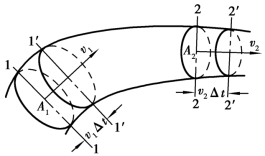
【摘要】：动量方程式流动液体的动量方程式是动量定理在流动液体中的应用,即在单位时间内流动液体的动量增量应等于该液体所受到的外力的和,用公式表示为:图1.12流动液体的动量方程如图1.12 所示,有一段不可压缩的液体在1—2管段中作稳定流动,在通流截面1—1 和2—2 处平均流速分别为v1 和v2,面积为A1、A2。

(1)动量方程式

流动液体的动量方程式是动量定理在流动液体中的应用,即在单位时间内流动液体的动量增量应等于该液体所受到的外力的和,用公式表示为:

pagenumber_ebook=23,pagenumber_book=17

图1.12　流动液体的动量方程

pagenumber_ebook=23,pagenumber_book=17

如图1.12 所示,有一段不可压缩的液体在1—2管段中作稳定流动,在通流截面1—1 和2—2 处平均流速分别为v1 和v2,面积为A1、A2。经过Δt 时间后,液体的位置从1—2 流到位置1′—2′。由于是稳定流动,故液体段1′—2′内各点的所有力学参数均未变化,其动量也未变化。这样,在时间Δt 内液体段1—2 的动量变化将等于2—2′液体段的动量与1—1′液体段动量之差,即

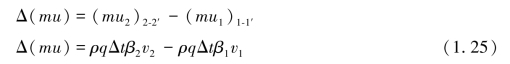
pagenumber_ebook=23,pagenumber_book=17

式中　m——液体段1—1′或2—2′的质量,m=ρv=ρqΔt;

ρ——液体的密度;

q——液体的流量;

β1、β2——用平均流速来代替真实流速u 的动量修正系数。紊流时,β = 1,层流时,β=1.33,为简化计算,β 值常取为1。

将式(1.25)代入式(1.24)得:

上式即为流动液体的动量方程。它是一个矢量方程,在应用时可根据具体情况将公式变成指定方向的动量方程式。

(2)动量方程的应用

1)油液流过90°弯管时对管壁的作用力

取图1.13 所示的弯管,其两端的通流截面为控制面,两通流截面的参数如图中所示。在稳定流动情况下,忽略其质量力,在x、y 方向列出动量方程如下:

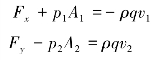
pagenumber_ebook=24,pagenumber_book=18

固体壁上所受作用力为Fx、Fy 的反力,即油液对管壁的压力。

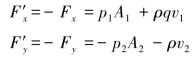
pagenumber_ebook=24,pagenumber_book=18

上式说明管壁所受的作用力由两部分组成,其一是由油液所产生的压力,其二是由于油液动量变化所产生的稳态液动力。

pagenumber_ebook=24,pagenumber_book=18

图1.13　流过90°弯管时对管壁的作用力

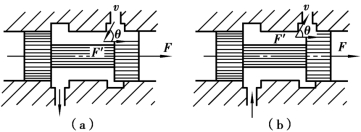
pagenumber_ebook=24,pagenumber_book=18

图1.14　滑阀上的液动力

2)油液作用在滑阀上的轴向液动力

如图1.14 所示的滑阀中,液体流动方向相反。现取进出口之间的液体作为控制体。

控制体内液流初速在轴向方向的分量v1=v cos θ,液流末速在轴向方向分量v2=0,因此阀芯受到轴向方向作用力F′为:

F′力的方向与v cos θ 同向,即阀芯上所受的稳态液动力力图使滑阀阀口关闭。

在图1.14(b)中,其滑阀阀芯受到轴向方向作用力F′为:

F′方向与v cos θ 方向相反,同样也说明F′力也力图使滑阀阀口关闭。

由以上分析可知,在一般情况下,液流通过阀口而产生对阀芯的轴向作用力(即液动力)都有使滑阀阀口关闭的趋势。