动量方程式流动液体的动量方程式是动量定理在流动液体中的应用,即在单位时间内流动液体的动量增量应等于该液体所受到的外力的和,用公式表示为:图1.12流动液体的动量方程如图1.12 所示,有一段不可压缩的液体在1—2管段中作稳定流动,在通流截面1—1 和2—2 处平均流速分别为v1 和v2,面积为A1、A2。......
2023-06-18
(1)理想液体的伯努利方程
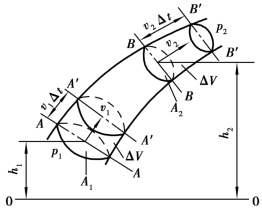
图1.10 理想液体伯努利方程推导
如图1.10 所示,设理想液体在管中作稳定流动,任取一段液流AB 作为研究对象,在很短的时间Δt 内,液体从管道AB 位置流到A′B′位置。设A、B 两截面中心到基准面0-0 的高度分别为h1、h2,通流截面面积分别为A1、A2,压力分别为p1、p2,平均流速分别为v1、v2,现对液体在管中流动时的能量变化进行分析。
1)作用在AB 段流体上的力所做的功
由于是理想液体,所以作用在流动液体上的力只有重力和压力。
①压力所做的功:因为理想液体无黏性,侧面压力不能产生摩擦力做功,只有作用于AB 段两端的通流截面上的压力p1 和p2 做功,则两截面上压力所做功的代数和,即
![]()
![]()
或
![]()
式中 ΔV——AA′或BB′微小段液体的体积。
故有
![]()
②重力所做的功:因为是理想液体作稳定流动,所以由AB 段经Δt 时间流动到A′B′段,其中A′B 在Δt 时间内位置不变。
重力所做的功为:
![]()
式中 Δm——AA′或BB′微小段液体的质量。
2)动能的增量
液体从AB 段移到A′B′,因是稳定流动,中间段A′B 液体的所有力学参数均未发生变化,故这段液体的动能没有增减。因而液体AB 段在Δt 时间流动时动能变化为:
![]()
根据动能定理,外力所做功的总和等于液体能量的增量,即
![]()
故有:
![]()
将上式两边分别除以Δmg,整理得:
![]()
或

式(1.21)和式(1.22)称为理想液体的能量方程,一般称为理想液体的伯努利方程。
伯努利方程中各项都代表一种形式的能量,而且都具有单位能量的意义,其单位为长度单位。其能量方程各项的名称为:
h:单位质量液体所具有的势能,称为比势能(位置头)。
![]() :单位质量液体所具有的压力能,称为比压能(压力头)。
:单位质量液体所具有的压力能,称为比压能(压力头)。
![]() 单位质量液体所具有的动能,称为比动能(速度头)。
单位质量液体所具有的动能,称为比动能(速度头)。
因此,理想液体伯努利方程物理意义是:在密闭管道内作稳定流动的理想流体具有3 种形式的能量,即势能、压力能和动能。三者之间在流动过程中可以相互转换,但其任一截面的总能量是常数。
(2)实际液体的伯努利方程式
由于实际液体在管中流动时存在黏性和可压缩性,运动时因摩擦要损耗部分能量,同时,管道的局部形状和尺寸的骤然变化,使液流产生扰动,也要损耗部分能量。如果将这些损耗的能量用hw 表示,则式(1.21)就可写成:
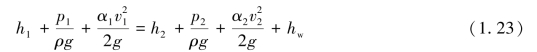
式中 α1、α2——动能修正系数。
由于截面上实际流速分布不均,用平均速度代替实际速度来计算动能时,必然会产生误差,所以在动能计算中,引入修正系数α1 和α2。对于紊流α=1,对于层流α=2(层流和紊流的意义见第四节)。式(1.23)称为实际液体的伯努利方程。
(3)伯努利方程式的应用条件及应用举例
在应用伯努利方程时,其应用条件是:
①液流必须是稳定流或近似稳定流。
②两通流截面应在渐变流段选取,但两段截面间的液流可以是渐变流,也可是急变流。
③液流是连续且不可压缩的,即ρ 为常数。
④液流在密闭管道中流动,各通流截面的流量q 为常数。
⑤忽略惯性力的影响,液体所受质量力只有重力。
例1.2 图1.11 所示为一液压泵的吸油装置。该泵的吸油管直径d=19 mm,油液的流量q=25 L/min,液压泵吸油口处允许最小绝对压力p2=6.3×104 Pa,油液密度ρ=900 kg/m3,各项压力损失总和为∑Δp =3×104 Pa(包括油液通过吸油管的压力损失、油管接头处的压力损失、滤油器的压力损失等)。试确定液压泵的吸油高度。
解 设油池液面为Ⅰ—Ⅰ截面,在该处认为v1=0,且p1=pa(大气压力),h1=0,取液压泵吸油口为Ⅱ—Ⅱ截面,v2 为吸油口处的液体流速,p2 为液压泵吸油口处压力,h2 为液压泵吸油高度。
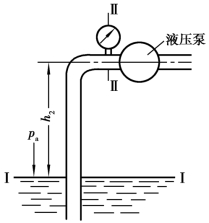
图1.11 液压泵吸油装置示意图
由截面Ⅰ—Ⅰ和Ⅱ—Ⅱ列伯努利方程:
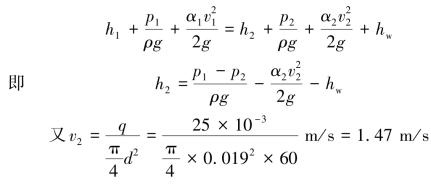
取α=2,则![]()

故
计算结果表明,为保证液压泵吸油口处的压力不低于允许的绝对压力值,泵的吸油高度必须有一定限制。一般液压泵允许的吸油高度以不超过0.5 m 为宜。
有关液压传动与控制(第2版)的文章

动量方程式流动液体的动量方程式是动量定理在流动液体中的应用,即在单位时间内流动液体的动量增量应等于该液体所受到的外力的和,用公式表示为:图1.12流动液体的动量方程如图1.12 所示,有一段不可压缩的液体在1—2管段中作稳定流动,在通流截面1—1 和2—2 处平均流速分别为v1 和v2,面积为A1、A2。......
2023-06-18

伯努利方程用于研究、设计与计算低速流体流动的问题时,通常计算结果和实际测量压力与速度值彼此之间的误差不大,但是对于某些时刻或精确度要求较高的工程问题研究方程必须做修正。当考虑流体的局部阻力损失时,理想流体的伯努利方程应该修正为式中hf与hζ分别为沿程水头损失与局部水头损失。......
2023-06-29

10.4.1.2推移质不平衡输沙方程窦国仁推移质不平衡输沙方程式为:式中:γ和γs分别为水和泥沙颗粒容重;Hw和T 分别为平均波高和周期;根据多处海域资料求得α0=0.023,β0=0.04fw,fw为波浪摩阻系数;谢才系数用满宁公式确定,即C为床面糙率系数。......
2023-06-22

研究低速流体力学问题的计算公式主要为流率守恒公式与伯努利方程式这两个,研究的重点放在流动流体流速和压力的变化上。对于低速流动,使用伯努利方程式研究流体流动时压力与速度的变化,其计算结果与实际测量结果之间的误差其实不大,以致于可以将误差忽略不计。......
2023-06-29

综上所述,异步电动机运行时从电源输入电功率P1到转轴上输出机械功率P2的全过程用功率平衡方程式表示为不难看出,在电力传动自动控制系统中,不论是采用直流电力传动,还是采用交流电力传动,系统的转矩和功率始终是保持平衡的,这是控制系统基本控制规律。......
2023-06-25

层流和紊流液体在管路中流动时,有两种不同的流动状态,即层流和紊流。图1.15雷诺实验装置在容器A 和B 中分别装满水及红色液体,阀K 可调节管C 中的水的流动速度。雷诺数根据实验,液体的流动状态是层流还是紊流,不仅与管内液体平均速度v 有关,并且与管子直径d 及液体运动黏度ν 有关,可以用雷诺数Re 作为判别流动状态的准则。表1. 4 为常见的管道临界雷诺数。......
2023-06-18

化学版式分为两大类:一类是无机化学版式,另一类是有机化学版式。前一类化学版式比较简单,但是首先需要掌握有关排版方面的化学知识。在化学式中称为“反应符号”。根据反应符号上方和下方“反应条件”的内容情况,反应符号可适当加长。化学反应式以“单行”公式为主,一律“居中”排。化学反应式过长,超出横版心的宽度,可以由反应符号后的内容回行居右整体居中排。图3-3化学反应式回行的版式反应条件的版式。......
2023-06-24
相关推荐