图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀,裂纹内气体体积可表述为式中,a为裂纹长度;W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点,爆燃反应冲击波呈球形在跑道各层介质中传播,产生径向压力波,强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中,A为混凝土面层反射系数。......
2023-06-18
活性聚能战斗部应用于反硬目标串联战斗部,前级聚能战斗部通过活性聚能侵彻体开孔后,后级杀爆战斗部随进目标内部发生爆炸,形成破片杀伤场和爆炸超压。随进子弹对靶后内部目标的毁伤效应取决于破片初速、破片分布密度、爆炸超压等参量,而这些参量均与后级弹径直接相关。也就是说,前级聚能战斗部开孔直径的大小直接决定了后级杀爆战斗部随进子弹的威力。
1.破片初速
破片初速是衡量破片杀伤威力的重要参数之一。根据能量守恒定律,战斗部装药爆炸后释放的总能量ET等于破片的动能Ec、爆轰产物的动能Eg、爆轰产物的内能Ee、壳体的变形能EM及壳体周围介质吸收的能量Ei之和。其中,Ee、EM和Ei占比很小,通常可忽略不计,则有
![]()
其中

式中,m为装药质量;Qv为炸药爆热;M为壳体质量;v0为破片初速;m1为爆轰产物虚拟质量(对圆柱形壳体,取m1=m/2;对球形壳体,取m1=3m/5)。
由式(6.16)~式(6.19),即可得破片初速

式中,![]() 为与装药有关的Gurney常数;β为装药与壳体质量比。
为与装药有关的Gurney常数;β为装药与壳体质量比。
与自然破片杀爆战斗部不同,反硬目标串联战斗部的后级杀爆战斗部随进子弹多采用预制破片形式。相比于自然破片,爆轰产物经预制破片的间隙泄漏较早,炸药爆炸能量利用率较低,导致其初速较低。研究表明,预制破片初速约为自然破片初速的0.7~0.9倍。预制破片初速计算公式具体可表述为
![]()
装填系数对预制破片初速的影响如图6.42所示。从图中可以看出,预制破片初速主要取决于装填系数β,随着β的增大,预制破片初速显著增加。随进子弹口径为35 mm时,装填系数为0.64,预制破片初速为1 667 m/s;随进子弹口径增加至50 mm时,装填系数增加至0.98,预制破片初速为1 940 m/s,较随进子弹口径为35 mm时增加17%。
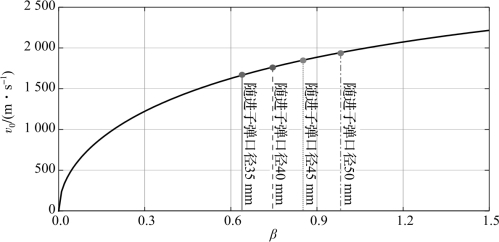
图6.42 装填系数对预制破片初速的影响
不同口径的随进子弹破片初速轴向分布如图6.43所示。随着随进子弹口径的增大,破片轴向初速均增大,在距起爆端2/3弹长处增幅最大。

图6.43 不同口径的随进子弹破片初速轴向分布
2.破片飞散角
破片飞散角主要描述以随进子弹重心为顶点,包含90%有效破片飞散区域的锥角。破片飞散角越小,表明破片飞散越密集,杀伤效果越佳。
壳体膨胀飞散几何关系如图6.44所示。主装药爆炸一段时间后,相当于将随进子弹轴线下移一段距离Δ=Kd/2,其中,d为随进子弹口径,K为与壳体材料有关的常数。假设壳体侧面与炸药接触部分为有效壳体,由有效壳体两端分别取5%截面积Sa、Sb,再从剩余壳体外表面端点a、b分别作与弹丸重心垂直偏移点O′的连线,夹角Ω即壳体破裂瞬间的破片飞散角。

图6.44 壳体膨胀飞散几何关系
随进子弹口径对破片飞散角的影响如图6.45所示,从图中可以看出,随子弹口径增大,破片飞散角近似呈二次抛物型递减。随进子弹口径由35 mm增加至50 mm时,破片飞散角由96°减小至72°,破片飞散密度显著增大。
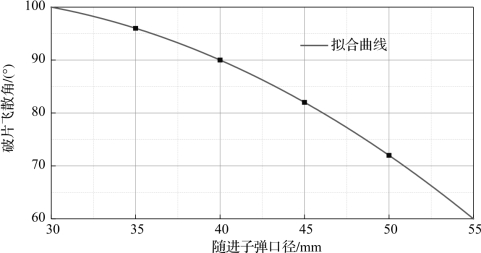
图6.45 随进子弹口径对破片飞散角的影响
3.破片分布密度
随进子弹爆炸后,破片呈球状向外扩散,分布密度表述为
![]()
式中,φ为破片飞散角;f(φ)为破片分布密度;σ为φ的均方差;φ为φ的数学期望。
不同口径的随进子弹破片分布密度如图6.46所示,随着随进子弹口径的增大,破片向中部集中,在小脱靶情况下,杀伤威力显著提升。
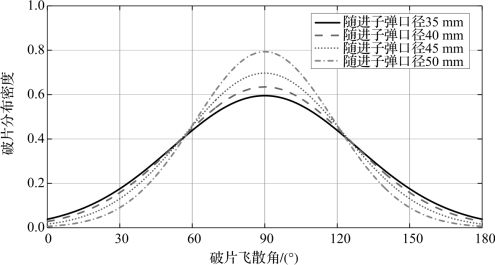
图6.46 不同口径的随进子弹破片分布密度
4.破片有效杀伤距离
破片在空中飞行的过程中,速度不断衰减,依靠其存速或剩余动能杀伤距离R处的目标。一定距离处,破片存速可表述为
![]()
式中,R为破片飞行距离(m);CD为破片形状系数;ρ为空气密度;S为破片迎风面积;q为破片质量;α为衰减系数。
破片剩余动能E可表述为
![]()
根据破片动能杀伤标准,在距离R处,当破片剩余动能大于或等于杀伤目标所需的最小动能Emin时即可杀伤目标,则杀伤条件可表述为
![]()
随进子弹口径对破片有效杀伤距离的影响如图6.47所示。随着随进子弹口径增加,破片初速及初始动能显著增大,随着破片飞散距离增加,动能快速衰减。随进子弹口径从35 mm增大至50 mm,破片有效杀伤距离增加60%~70%。
5.破片空间杀伤区
破片空间杀伤区指以破片等杀伤概率曲线所围成的区域,杀伤概率p=0.5的曲线所包络区域为有效杀伤区,p=0.9的曲线包络区域为密集杀伤区。
以战斗部重心为圆心,以破片飞行距离R为半径的球面如图6.48所示,图中,φ为破片飞散角,ΔSi为球面上任一球带微元面积。
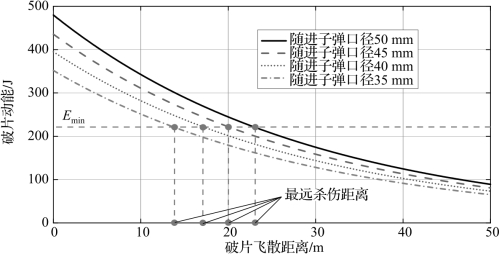
图6.47 随进子弹口径对破片有效杀伤距离的影响
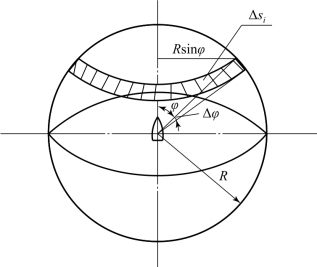
图6.48 破片飞散球面
球带Δφ内有效破片数为Nei,球带面积为ΔSi,有效破片平均分布密度为
![]()
其中
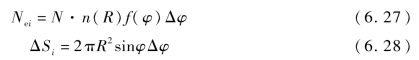
式中,N为破片总数;f(φ)为破片飞散密度函数;n(R)为相对有效破片数。
破片初速为v0,经一定衰减后,飞行至距炸点R处与目标作用。根据破片动能杀伤准则,此时破片动能应不小于杀伤目标所需的最小动能Emin。
基于该准则,破片初速必须大于某一临界值v0e,才可满足杀伤距炸点R处目标的动能标准,可表述为
![]()
![]()
式中,Emin,q、α分别为目标临界毁伤动能、破片质量和破片速度衰减系数。
以v0e作水平线,沿两交点分别作垂线与坐标横轴相交,坐标差值(x2-x1)/l即相对有效破片数,如图6.49所示。

图6.49 破片初速与有效破片数的关系
由式(6.26)~式(6.28),可得

其中
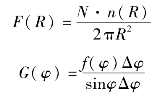
假设目标垂直于破片飞散方向的投影面积为S0,则命中该目标的有效破片数为εS0,则至少有一块有效破片命中目标的概率p可表述为
![]()
目标给定时,S0为定值,将式(6.31)代入式(6.32),可得
p=1-e-S0F(R)G(φ)
对上式移项并取对数,可得

令p=p1,可作-ln(1-p1)/S0G(φ)与φ关系曲线,给定不同的p1值,随进子弹F(R)与R、-ln(1-p1)/S0G(φ)与φ的关系曲线如图6.50所示。
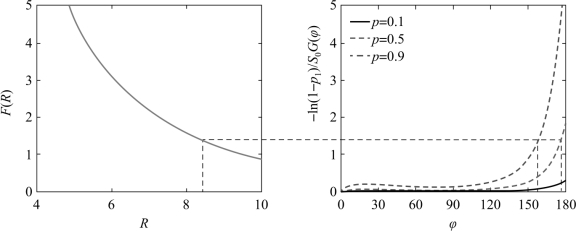
图6.50 随进子弹F(R)与R、-ln(1-p1)/S0 G(φ)与φ关系曲线
任取一φ1值,可求出对应于某一杀伤概率p1的-ln(1-p1)/S0G(φ)值,再由-ln(1-p1)/S0G(φ)引水平线与F(R)曲线相交,可得与φ1对应的R1值。类似地分别求得φ2、R2;φ3、R3等,然后以战斗部重心为中心,按φ1、φ2、φ3等值分别作出半径R1、R2、R3等,最后将R1、R2、R3等端点连成曲线,此曲线所包括的范围就是等杀伤概率p1的杀伤区域。
严格来讲,等概率杀伤区域是绕战斗部轴线的一个对称曲面,在该曲面边界,破片对目标的杀伤概率为一定值pi,给定不同的pi值,可求得等杀伤概率曲线的空间分布规律。不同口径随进子弹50%有效杀伤概率曲线空间分布如图6.51所示,由图可知,随进子弹口径增大可显著提高有效杀伤区域。
6.破片场威力半径
破片场是战斗部杀伤威力的综合性参数,本身包含对破片动能Ey、破片密度ε的要求。战斗部爆炸后形成的破片在一定飞散角Ω内分布形成球缺分布面。在破片数一定的条件下,破片密度ε随着飞行距离的增加而减小。为了确保破片能有效命中目标,ε不能小于某一极值,可表述为
![]()
式中,Ne为有效破片数;S为球缺表面积,具体可表述为
![]()
式中,Ω为破片飞散角;φ1为飞散角下边缘与轴线交角。
将式(6.35)代入式(6.34),整理得
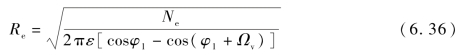
式中,Re为破片场威力半径。
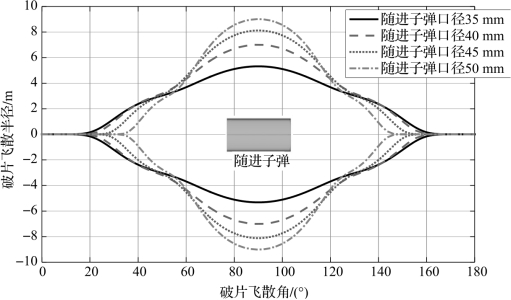
图6.51 不同口径随进子弹50%有效杀伤概率曲线空间分布
随进子弹口径对破片威力场半径的影响如图6.52所示,在不同ε取值条件下,随着随进子弹口径增加,破片威力场半径显著增加。以破片密度ε=1为例,随进子弹口径从35 mm增加至50 mm,破片场威力半径可增大1倍左右。

图6.52 随进子弹口径对破片场威力半径的影响
着眼于两级体制反硬目标串联战斗部,前级聚能战斗部可首先通过活性聚能侵彻体动能与爆炸化学能联合作用,显著增加对防护功能型硬目标开孔孔径,使后级杀爆战斗部随进子弹口径显著增加,破片初速、破片有效杀伤距离、破片威力场半径等显著增加,从而大幅提升对靶后目标杀伤效应。
有关活性毁伤增强聚能战斗部技术的文章

图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀,裂纹内气体体积可表述为式中,a为裂纹长度;W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点,爆燃反应冲击波呈球形在跑道各层介质中传播,产生径向压力波,强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中,A为混凝土面层反射系数。......
2023-06-18

实验中,活性药型罩聚能战斗部放置于坦克靶标首上装甲位置,在坦克靶标内驾驶位、炮手位、车长位分别放置活羊,以研究活性药型罩聚能战斗部对有生力量后效杀伤效应。活性药型罩聚能战斗部通过电雷管及起爆药引爆,实验过程通过高速摄影记录,实验后打开驾驶舱,检查有生力量杀伤效应。活性聚能侵彻体主要通过爆燃反应产生的显著超压效应,实现对有生力量的杀伤效应。......
2023-06-18

图2-44卫星网络HTTP增强技术2.4.3.2Web缓存技术Web缓存的核心思想是“取一次、用多次”,利用访问数据的可复制性和共享性,将用户访问频率高的内容保存到离用户较近的缓存中,当用户再次访问时,就可以用较低的代价快速获取。......
2023-07-02

以上实验结果均表明,活性聚能侵彻体可对装甲防护下的电子元器件产生高效毁伤效应。图3.34活性药型罩聚能装药毁伤技术装备实验原理图3.35活性聚能侵彻体对钢板毁伤效应图3.36活性聚能侵彻体对密闭箱体毁伤效应图3.37活性聚能侵彻体对间隔铝靶毁伤效应图3.38活性聚能侵彻体对电路板毁伤效应3.毁伤增强机理活性聚能侵彻体穿透靶板后在密闭箱体内发生剧烈化学反应,释放大量能量,产生高温气体,在密闭空间内形成高幅值超压。......
2023-06-18

可用以衡量塑料强度相关性能的指标主要有拉伸强度、断裂伸长率、弯曲强度及其弯曲模量等。关于塑料增强的机理,目前还未取得共识,这里只介绍几种常见的理论。④叠层增强技术:采用同一种或者不同种塑料,通过特殊的叠层工艺复合方式,实现材料的多级叠层复合,达到增强的效果,目前可以实现超过1万层的复合。......
2023-06-26

一般凡能提高基体材料力学性能的物质均称为增强材料。以树脂为基体、用作结构件的复合材料,大都以纤维材料作为增强材料。如某原纱的支数为160支,即表示该种原纱1 g重长度为160 m。碳纤维的密度较小,密度为1.5~2.1 g/cm3。通用级碳纤维是拉伸强度小于1.0 GPa、拉伸模量小于100 GPa 的碳纤维;高性能碳纤维包括中模型、高模型、超高模型、高强型和超高强型碳纤维。......
2023-07-18

在DTVGM模型中,产流发生在每个单元,在垂向上分为地表径流、壤中流和地下径流。DTVGM单元产流模型结构如图5-2-1所示。图5-2-1DTVGM单元模型结构图1.地表水产流单元地表水产流量根据时变增益非线性产流的概念按下式计算。......
2023-06-25

AR技术有比较长的历史,从广义上讲,凡是在现实环境的影像上附加额外信息的应用都算AR。早期的AR系统应用范围比较局限,普通大众了解不多,主要应用在少数工业制造维修或类似场景中。2013年,谷歌计划推出谷歌眼镜,引发市场对AR技术的关注。机构甚至因此调高了AR市场预期;巨头看好AR市场,纷纷提前布局底层技术,加速了AR市场教育。与此同时,国内增强现实初创厂商纷纷入场,先行布局AR市场,期望在巨大的AR市场中分得一杯羹。......
2023-08-18
相关推荐