当堆积在侵孔内的活性材料发生剧烈爆燃反应时，侵孔内压力骤升，孔壁承受高幅值载荷，导致钢靶产生贯穿裂纹或发生严重碎裂。裂纹扩展过程如图4.25所示，钢靶膨胀至某一临界状态时，假设裂纹随机出现于A、B两点，如图4.25所示。图4.26钢靶爆裂模型计算与实验结果对比需要特别说明的是，钢靶碎裂行为理论模型存在一定的局限性。......
2025-09-29
毁伤增强模型的优化方案
【摘要】：图5.37混凝土面层爆破及裂纹扩展模型假设爆燃反应气体产物等熵膨胀，裂纹内气体体积可表述为式中，a为裂纹长度；W为活性聚能侵彻体爆燃反应深度。图5.39环向裂纹及抛掷效应分析模型以有效活性聚能侵彻体等效起爆中心为原点，爆燃反应冲击波呈球形在跑道各层介质中传播，产生径向压力波，强度随传播距离衰减。图5.40混凝土面层底部压力分布模型作用于混凝土面层垂直方向的作用力分量可表述为式中，A为混凝土面层反射系数。
1.径向裂纹模型
活性聚能侵彻体侵至跑道一定深度后，活性材料发生爆燃反应。在爆燃强冲击波作用下，混凝土面层出现初始裂纹，在爆燃气体产物膨胀时，裂纹进一步扩展，形成破碎区，如图5.37（a）所示，裂纹如图5.37（b）所示。
图5.37 混凝土面层爆破及裂纹扩展模型
假设爆燃反应气体产物等熵膨胀，裂纹内气体体积可表述为
式中，a为裂纹长度；W为活性聚能侵彻体爆燃反应深度。
活性聚能侵彻体反应产生的压力可表述为
式中，γ为气体绝热指数；V0为侵孔体积；meff为进入侵孔内的有效活性聚能侵彻体质量；e为活性材料比内能。
随着裂纹扩展，裂纹尖端处加载强度逐渐降低，加载压力可表述为
裂纹扩展停滞时，应力强度因子KIC可表述为
根据式（5.44）～式（5.47），裂纹长度方程可表述为
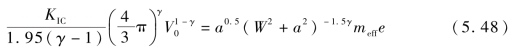
式（5.48）表明，活性聚能侵彻体爆燃引起混凝土面层形成的裂纹长度与起爆深度、动能侵孔体积和活性聚能侵彻体有效质量等因素密切相关。
2.面层隆起模型
在活性聚能侵彻体爆燃反应超压作用下，混凝土面层隆起效应如图5.38所示，研究表明，混凝土面层的变形量与爆燃反应超压冲量成正比，与混凝土面层材料密度和厚度成反比，则隆起变形量可表述为
式中，A 为常数；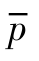
为平均作用压力；
为有效作用时间；ρc为混凝土面层材料密度。
由于活性聚能侵彻体爆燃反应时间为微秒量级，与爆燃作用持续时间（毫秒量级）相比可忽略不计，因此可忽略活性聚能侵彻体尺寸的影响，假设爆燃载荷有效作用时间为常数。此外，混凝土面层所受平均载荷作用压力p-与最大压力p成正比，式（5.49）可简化为
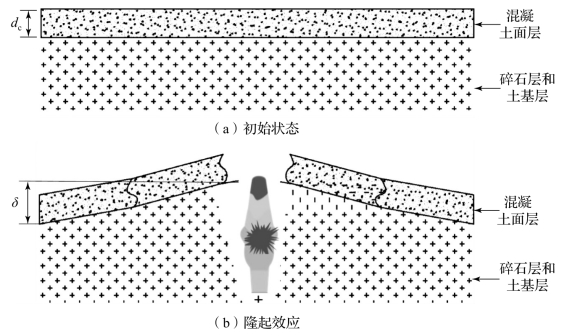
图5.38 混凝土面层隆起效应分析模型
混凝土面层所受最大压力可表述为
则混凝土面层隆起变形量可表述为
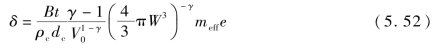
对于给定厚度的混凝土面层，隆起变形量可简化为
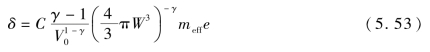
式中，C为常数，与混凝土面层厚度、材料密度和爆燃载荷作用时间有关。(https://www.chuimin.cn)
式（5.53）表明，混凝土面层的隆起变形量除与动能侵孔体积和起爆深度有关外，还显著受进入跑道目标内活性聚能侵彻体有效质量的影响。
3.环向裂纹及抛掷模型
具有一定长度的活性聚能侵彻体在跑道目标内一定深度处发生爆燃反应，混凝土面层环向裂纹的产生主要由活性聚能侵彻体爆燃反应冲击波超压造成。
假设起爆中心为混凝土面层下的有效活性聚能侵彻体几何中心，起爆深度为dp，环向裂纹半径为r，环向裂纹及抛掷效应分析模型如图5.39所示。
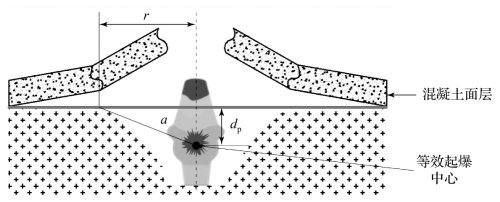
图5.39 环向裂纹及抛掷效应分析模型
以有效活性聚能侵彻体等效起爆中心为原点，爆燃反应冲击波呈球形在跑道各层介质中传播，产生径向压力波，强度随传播距离衰减。当压力波传至混凝土面层底部时，作用在混凝土面层底部的作用力可表述为
以上作用力与作用时间、跑道几何结构等有关，当局部剪切力大于面层混凝土屈服强度时，混凝土面层开始变形隆起。在活性聚能侵彻体爆燃反应瞬间，起爆点正上方压力最大，随着时间及距离r增加，爆燃压力逐渐降低。当作用于混凝土面层的压力大于其抗拉强度时，混凝土面层结构失效，产生环向裂纹。爆炸冲击波进一步作用，失效混凝土产生抛掷效应。
作用于混凝土面层的冲击波导致介质运动，介质失效时，对应临界粒子速度vc可表述为
式中，σu为面层混凝土的最大动态抗拉强度。
由此可得出，引起混凝土面层结构失效的临界冲量可表述为
有效活性聚能侵彻体爆燃冲击波作用于混凝土面层底部，作用载荷可等效为环形分布的压力载荷，压力分布模型如图5.40所示。
实际作用于混凝土面层底部的冲量可表述为
根据霍普金斯方程，距起爆点x远处的压力可表述为
式中，P为起爆点处的峰值压力。
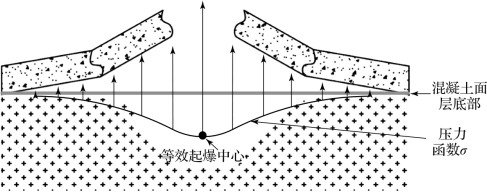
图5.40 混凝土面层底部压力分布模型
作用于混凝土面层垂直方向的作用力分量可表述为
式中，A为混凝土面层反射系数。
式（5.59）表示以某点为起爆中心，作用力仅为传播距离r的空间函数。该力的作用时间可表述为
式中，tp为冲击波到达混凝土面层底部的时间；tr为冲击波持续作用时间。
联立式（5.59）和式（5.60），可得
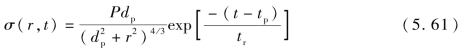
在实际分析中，起爆深度dp可通过数值模拟获得，将dp代入式（5.61）和式（5.57），r值与混凝土面层厚度相同，通过式（5.57）即可获得作用于混凝土面层的冲量。与混凝土面层失效临界冲量Ic比较，若小于Ic，混凝土面层将不会发生结构失效；但若远大于Ic，则增大r值，对式（5.61）进行积分，直至冲量约近似等于Ic，此时对应的r值即失效混凝土面层的最大半径。
相关文章
- 详细阅读
-
间隔靶毁伤的增强效应优化探索详细阅读
图4.27活性聚能战斗部对间隔靶毁伤效应实验方法实验中，活性聚能战斗部口径为48 mm，在炸高筒的支撑下，置于多层间隔靶顶部15 mm厚的45钢钢锭上。实验结果表明，与铜射流相比，活性聚能侵彻体能够产生明显的后效增强毁伤效应。图4.31铜药型罩聚能装药对间隔靶毁伤效应......
2025-09-29
-
技术装备的毁伤增强效应优化方法详细阅读
以上实验结果均表明，活性聚能侵彻体可对装甲防护下的电子元器件产生高效毁伤效应。图3.34活性药型罩聚能装药毁伤技术装备实验原理图3.35活性聚能侵彻体对钢板毁伤效应图3.36活性聚能侵彻体对密闭箱体毁伤效应图3.37活性聚能侵彻体对间隔铝靶毁伤效应图3.38活性聚能侵彻体对电路板毁伤效应3.毁伤增强机理活性聚能侵彻体穿透靶板后在密闭箱体内发生剧烈化学反应，释放大量能量，产生高温气体，在密闭空间内形成高幅值超压。......
2025-09-29
-
活性聚能的毁伤机理优化方案详细阅读
图1.44活性药型罩聚能装药毁伤威力及性能要求抗过载能力。活性药型罩材料应具有一定的激活延时特性，在活性聚能侵彻体成形阶段尽量不发生反应，而侵入目标内适时发生爆燃反应，从而实现动能侵彻和爆燃化学能的双重高效毁伤机理。图1.46活性聚能侵彻体对本体功能型目标毁伤机理打击机库类目标，开孔大，后效毁伤强。......
2025-09-29
-
应急大数据存储模型优化方案详细阅读
应急大数据种类多，关系复杂。该混合时空数据模型将应急时空大数据抽象为数据集{时间，空间，事件}，如图2.10所示。其中时间轴T为UTC时间，空间轴X为与突发事件相关的空间基础数据，存储形式为CGCS2000坐标系下的大地坐标，事件轴E是突发事件的相关数据，主要包括致灾因子、承灾体、孕灾环境、抗灾体等数据。将X及E投影到时间轴，可视为在某一时间节点上的快照片段数据，表达为该时刻发生事件涉及的空间区域以及应急数据。......
2025-09-29
-
钢靶毁伤增强效应的研究详细阅读
炸高为0.5 CD、1.0 CD与1.5 CD时，在动能与化学能联合作用下，爆裂毁伤效应导致钢靶裂为多个碎块。实验结果列于表4.2，在不同炸高条件下钢靶毁伤效应如图4.17所示，钢靶侵孔剖面如图4.18所示。从图4.17可以看出，在不同炸高条件下，活性聚能战斗部对钢靶毁伤增强效应显著不同。......
2025-09-29
-
间隔靶毁伤增强机理的分析介绍详细阅读
图4.34各层靶板毁伤效应表4.6铜射流侵彻间隔靶数值模拟与实验结果对比2.活性聚能侵彻体毁伤增强机理活性聚能侵彻体利用动能和爆炸化学能耦合作用，实现对间隔靶的毁伤增强。图4.36活性聚能侵彻体作用间隔靶毁伤增强机理在活性聚能侵彻体侵爆耦合毁伤阶段，活性聚能侵彻体到达反应弛豫时间，剩余活性聚能侵彻体与靶后形成的活性材料碎片云剧烈爆燃。......
2025-09-29
-
优化载荷子输运模型的研究详细阅读
单极电荷的输运的数学公式已经被提出。目前，仍未出现同时考虑双极电流、输入受限输运和整体受限输运的统一模型。空穴输运在低能级上完成，所以空穴对因氧气等环境因素而产生的陷阱不敏感。相反，电子对距离较近的这类陷阱敏感并总是表现出弥散输运行为。该理论对OLED的输运描述而言是有价值的。同时，其他研究小组保留了SCLC理论的有效性，并且将迁移率与电场的关系包含在内，这种关系目前是强制性的。......
2025-09-29
相关推荐