图4.20复合结构活性药型罩聚能装药对钢靶毁伤效应图4.21活性聚能战斗部作用钢靶毁伤原理对于所给定的聚能装药结构，炸高对活性聚能侵彻体成形和侵彻效应影响显著。由于反应弛豫时间存在，活性聚能侵彻体发生化学反应之前，才能对目标产生类似惰性侵彻体的侵彻毁伤行为。由图4.23还可得到，活性聚能侵彻体侵彻钢靶的侵彻规律与金属铜射流大致相同，即侵彻深度随着侵彻时间呈指数增长趋势。......
2023-06-18
侵彻作用模型的探讨与优化
【摘要】：跑道由混凝土层、碎石层、土基层构成，活性聚能侵彻体作用跑道时，产生压缩波，形成压缩区。图5.35活性聚能侵彻体侵彻跑道模型微元i开始侵彻靶板时，侵彻深度为Pi-1，则微元i到达目标的时间表述为对于活性聚能侵彻体，由于反应弛豫时间τ的存在，当ti≥τ时，侵彻结束，此时侵彻深度即Pi-1；当ti＜τ时，侵彻继续进行。当考虑反射波的影响时，绝对侵彻速度按式～式计算；当考虑透射波的影响时，绝对侵彻速度按式～式计算。
跑道由混凝土层、碎石层、土基层构成，活性聚能侵彻体作用跑道时，产生压缩波，形成压缩区。随着压缩波传播至混凝土面层/碎石层、碎石层/土基层界面时，会发生透射和反射，使混凝土面层、碎石层和土基层的应力状态发生变化，从而影响活性聚能侵彻体对跑道目标的侵彻过程。
活性聚能侵彻体跑道的过程中，混凝土面层/碎石层界面对冲击波传播过程的影响如图5.34所示。压缩波到达混凝土面层/碎石层界面时，形成透射波和反射波，侵彻混凝土面层稳定的应力状态因界面扰动发生显著变化。
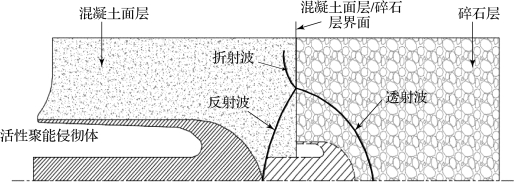
图5.34 混凝土面层/碎石层界面对冲击波传播过程的影响
1.压缩波的传播与衰减
活性聚能侵彻体作用跑道目标时，假设压缩波波速恒定，基于伯努利方程，活性聚能侵彻体与跑道作用点处的压力可表述为
式中，p0为侵彻压力；ρj为活性聚能侵彻体密度；vj为活性聚能侵彻体速度；u为侵彻速度。
侵彻产生的压缩波服从指数衰减规律，侵彻压力可表述为
式中，pK为压缩波压力；k为压缩波传播距离；γ为压缩波衰减系数。
当压缩波强度衰减至与弹性区/压缩区边界动态屈服强度相同时，弹性区/压缩区边界与初始扰动点间的距离I表述为
式中，Yt为靶板动态屈服强度。
从压缩波产生至其转变为弹性波，传播时间Δt为
式中，Cp为压缩波波速。
该时间段内，活性聚能侵彻体穿透深度ΔP可表述为
由式（5.4）～式（5.5），可获得弹性区/压缩区边界与初始侵彻界面间的距离为
对于侵彻轴线上的某点A，假设该点到侵彻界面的距离为x。考虑到多普勒效应，从初始扰动点到点A压缩波传播距离可表述为
将式（5.1）代入式（5.2），则点A处压力为
根据伯努利方程，点A处的粒子速度可表述为
式中，ρt为靶板密度；va为点A处粒子速度。
由于pA=p0，可得va=u，即侵彻界面处粒子速度与侵彻速度相等。
2.界面效应影响
根据混凝土面层/碎石层界面到侵彻界面的距离，基于波的反射和透射理论，结合式（5.8）和式（5.9），反射波、透射波、入射波压力与粒子速度的关系为
式中，下标I、R和T分别表示入射波、反射波和透射波；CC和CS分别为混凝土面层和碎石层压缩波波速；ρC和ρS分别为混凝土面层和碎石层密度。pI=pA，vI=va时，根据式（5.10）和式（5.11）可计算出反射波和透射波参数。
当混凝土面层/碎石层界面与侵彻界面距离为x时，vT同时为透射波中的粒子速度与界面运动速度。由于反射波与透射波方向相反，当反射波到达侵彻界面时（在混凝土面层中传播距离为c），对应压力和粒子速度分别为
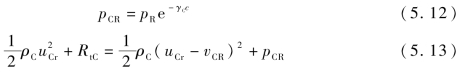
式中，γC为混凝土面层中压缩波衰减系数。
式（5.13）左边为反射波总压力，可进一步表述为
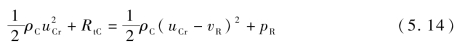
式（5.14）表明，在混凝土面层/碎石层界面处反射波的影响下，混凝土面层中初始压力和速度变为pCR和vCR，则活性聚能侵彻体和混凝土面层的相对速度关系为
活性聚能侵彻体在混凝土面层中的侵彻方程可表述为
式中，uCr为侵彻界面与混凝土面层的相对速度。在反射波的影响下，活性聚能侵彻体对混凝土介质的绝对侵彻速度表述为
反射波作用下粒子速度与侵彻速度方向相反，因此式（5.17）表明，混凝土面层/碎石层界面的存在，降低了活性聚能侵彻体对混凝土面层的侵彻速度。此外，侵彻界面与混凝土面层/碎石层界面靠近时，侵彻速度随反射波的增强而明显降低。
透射波对侵彻过程也有影响，当透射波在碎石层中传播距离为s时，对应的压力和粒子速度分别表述为
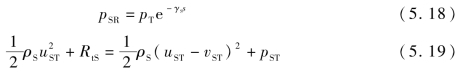
式中，γS为碎石层压缩波衰减系数。
式（5.19）左边为透射波总压力，可进一步表述为
式（5.20）表明，由于透射波的影响，碎石层中有初始压力pST和初始速度vST，则活性聚能侵彻体和碎石层的相对速度关系为
活性聚能侵彻体在碎石层中的侵彻方程可表述为
式中，uSr为侵彻界面相对于碎石层的相对速度。在透射波的影响下，活性聚能侵彻体对碎石介质的绝对侵彻速度可表述为
分析表明，在混凝土面层/碎石层界面效应的影响下，活性聚能侵彻体对碎石层的侵彻速度显著减小，侵彻深度小于对单层混凝土介质的侵彻深度。
基于相同的分析过程，当活性聚能侵彻体穿过碎石层/土基层界面时，活性聚能侵彻体对土基层的绝对侵彻速度也可按上述理论进行分析。
3.侵彻深度模型
活性聚能侵彻体侵彻跑道模型如图5.35所示，由于各微元存在速度梯度，活性聚能侵彻体会不断拉伸变长。将活性聚能侵彻体划分为n个微元，对任一微元i，与混凝土面层距离为zi，平均速度为vji（假设侵彻过程中各微元平均速度恒定），直径为Di，长度为Δli，以上微元参数均可通过数值仿真或实验确定。
由于活性聚能侵彻体不断拉伸，微元i到达靶板时的长度可表述为
式中，Δvi为微元i头部与尾部速度差，Δvi=vji-vji-1。
图5.35 活性聚能侵彻体侵彻跑道模型
微元i开始侵彻靶板时，侵彻深度为Pi-1，则微元i到达目标的时间表述为
对于活性聚能侵彻体，由于反应弛豫时间τ的存在，当ti≥τ时，侵彻结束，此时侵彻深度即Pi-1；当ti＜τ时，侵彻继续进行。
对于活性聚能侵彻体任一微元i，其侵彻深度可表述为
式中，Δti为微元i的侵彻时间；ui为微元i的绝对侵彻速度。
当考虑反射波的影响时，绝对侵彻速度按式（5.15）～式（5.17）计算；当考虑透射波的影响时，绝对侵彻速度按式（5.21）～式（5.23）计算。
根据微元i的长度ΔLi和入射速度vji-ui，侵彻时间可表述为
微元i完成侵彻时，活性聚能侵彻体的侵彻深度为
当活性聚能侵彻体的侵彻时间ti+Δti≥τ时，侵彻结束，此时侵彻深度即Pi；若ti+Δti＜τ，侵彻继续进行，侵彻过程依然按式（5.24）～式（5.25）计算，直至侵彻时间大于侵彻体的反应弛豫时间，侵彻结束。
有关活性毁伤增强聚能战斗部技术的文章
- 详细阅读
-
类射流活性聚能侵彻体释能模型探析详细阅读
与此同时，活性聚能侵彻体后部杵体形成，变形过程中温度继续升高，由于未到达激活弛豫时间，未发生反应。图3.2类射流活性聚能侵彻体化学能分布式释放计算模型根据类射流活性聚能侵彻体的形状，其可分为头部、中部及杵体3部分。式即类射流活性聚能侵彻体化学能随时间分布释放模型。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
类弹丸聚能侵彻体释能模型的活性分析详细阅读
类弹丸活性聚能侵彻体化学能分布式释放过程如图3.3所示。爆轰波完全扫过活性药型罩后，罩体内压力及温度进一步升高，活性药型罩顶部发生明显形变，在轴线处发生翻转，形成类弹丸活性聚能侵彻体头部。基于以上假设，以侵彻体尾部端面中点为原点，建立二维平面物质坐标系，类弹丸活性聚能侵彻体化学能分布式释放计算模型如图3.4所示。在继续成形过程中，侵彻体中部及尾裙部分温度逐渐升高，相继发生激活。......
2023-06-18
-
聚能射流侵彻的理论探究详细阅读
图1.26聚能射流典型破甲过程示意基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。以上原因均表明，射流断裂后，侵彻能力将大幅下降。图1.28断裂射流侵彻模型设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。......
2023-06-18
-
杆式射流的侵彻理论详解详细阅读
图1.32杆式射流侵彻理论模型建立过程1.等速等截面杆侵彻模型杆式射流侵彻靶板时，杆式射流沿长度方向可划分为多个连续微元，各微元长度在侵彻前已知，且各微元内直径和速度相同，如图1.33所示。图1.33等速等截面杆微元划分计算时，若忽略“开坑”阶段的能量损失，可认为杆式射流立即达到侵彻速度，杆式射流每一个微元对靶板侵彻，均可看作射流定常侵彻过程。将各段“杆元”侵彻深度之和作为杆式射流总侵彻深度。......
2023-06-18
-
缩比弹侵彻混凝土靶的实验设计优化详细阅读
利用北京理工大学爆炸科学与技术国家重点实验室φ152 mm 一级轻气炮开展了缩比弹侵彻混凝土靶板的实验，实验中轻气炮采用高压氦气作为发射气体。其中1、2、3号缩比弹的装药为三段，4号缩比弹装药为两段。表5－1缩比弹装药结构设计混凝土靶直径120 cm、厚150 cm，材料强度35 MPa，不配筋，最大骨料尺寸约2 cm，骨料按级配加入，靶体外部包有2 mm 厚的钢板，混凝土靶板如图5－4 所示。图5－4实验所用的混凝土靶板......
2023-06-27
-
深入探讨内爆作用模型详细阅读
到达活性材料反应弛豫时间后，进入侵孔的活性聚能侵彻体发生爆燃反应，释放大量化学能及气体产物，在侵彻毁伤的基础上，对混凝土面层进行二次内爆毁伤，导致跑道产生裂纹或抛掷效应。图5.36活性聚能侵彻体有效质量分析模型侵彻前，活性聚能侵彻体各微元体积可表述为式中，w0为活性聚能侵彻体微元所对应直线斜率。......
2023-06-18
-
类杆流活性聚能侵彻体释能模型探析详细阅读
图3.5类杆流活性聚能侵彻体化学能分布式释放过程虽然各微元速度梯度较类射流活性聚能侵彻体明显更小，但类杆流活性聚能侵彻体在运动及成形过程中不断拉伸延长，在t2时刻，长度为L2。在继续拉伸过程中，类杆流活性聚能侵彻体逐渐形成，整体密度降低，且由外至内、由头部至尾部，密度均逐渐下降。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
相关推荐