图7-21 热稳定性计算流程图最后，总载荷时间超过1s，计算结束，获得各个载荷步内电流有效值、导体温度、电动斥力矩、侧偏力矩和滑动力矩的分布规律。此外，为了考虑短时耐受过程初始阶段暂态电流对热稳定性的影响，依据三相暂态电流表达式，利用等效原则，将60ms时间内各个载荷步内短路电流换算为正弦电流进行加载。......
2025-09-29
钢靶爆裂毁伤模型优化探究
【摘要】：当堆积在侵孔内的活性材料发生剧烈爆燃反应时，侵孔内压力骤升，孔壁承受高幅值载荷，导致钢靶产生贯穿裂纹或发生严重碎裂。裂纹扩展过程如图4.25所示，钢靶膨胀至某一临界状态时，假设裂纹随机出现于A、B两点，如图4.25所示。图4.26钢靶爆裂模型计算与实验结果对比需要特别说明的是，钢靶碎裂行为理论模型存在一定的局限性。
在活性聚能侵彻体的作用下，钢靶毁伤主要由两部分组成，一是活性聚能侵彻体动能侵彻产生的具有一定深度和直径的侵孔，但未贯穿钢靶；二是堆积于侵孔底部的活性材料，爆燃反应导致侵孔内压力骤升，对钢靶造成二次结构破坏。
活性聚能侵彻体头部速度高，高速侵彻靶板是一个向密闭空间输入活性材料的过程。当堆积在侵孔内的活性材料发生剧烈爆燃反应时，侵孔内压力骤升，孔壁承受高幅值载荷，导致钢靶产生贯穿裂纹或发生严重碎裂。为了便于分析，假设侵孔为圆柱形。基于内爆载荷作用下结构破裂理论，钢靶爆裂过程可分为弹塑性膨胀、动态裂纹生成、裂纹扩展和结构爆裂4个阶段。
活性聚能侵彻体在侵孔内剧烈爆燃，爆轰波作用于侵孔内壁面形成压缩应力波，在介质中产生动态应力场，侵孔内表面承受高幅值载荷后发生塑性流动，引起剪切破坏，在侵孔内壁面首先产生裂纹，并快速扩展。裂纹无法进一步在压缩区扩展后，裂纹边界处产生卸载波，裂纹则无法进一步扩展传播。
裂纹扩展过程如图4.25所示，钢靶膨胀至某一临界状态时，假设裂纹随机出现于A、B两点，如图4.25（a）所示。A、B出现裂纹之后，立即出现两种新的情况，一是在裂纹两边的材料中产生卸载波，随卸载波运动形成卸载区；二是爆轰产物沿裂纹向外流动，压力迅速下降。随之，可能在C、D、E点出现裂纹，如图4.25（b）所示，类似地，会在裂纹两边形成新的卸载区，导致爆轰产物压力进一步下降。随后，在F点或G点出现裂纹，如图4.25（c）所示，卸载区的继续形成导致爆轰产物压力继续下降。卸载波未扫略区域，会出现新的裂纹，卸载波扫过全部钢靶后，破坏过程结束，如图4.25（d）所示。
假设卸载区宽度为x，由牛顿第二定律，钢靶爆裂过程运动方程可表述为
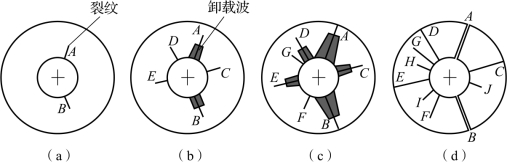
图4.25 厚钢靶侵彻入孔面裂纹形成与扩展过程
式中，σb为钢靶材料强度极限（MPa）；S为卸载区纵断面积（cm2）；t为卸载区宽度由0增至x所需时间（s）；dx/dt代表弧长x的切向变形速度，有dx/dt=xv0/r，r表征侵孔平均半径（cm）。
对式（4.17）积分，在时间0至t内，卸载区宽度由0增至x。当钢靶上出现裂纹后，可以近似认为v0与r保持不变，则钢靶碎片宽度可表述为
式中，ε为钢靶膨胀出现裂纹后任意时刻的应变；εk为钢靶材料临界应变。
假设S=Kε，一般
取则钢靶碎片平均宽度x0可表述为
堆积于侵孔内的活性材料瞬时发生爆燃反应，侵孔通道为圆柱形，带侵孔钢靶可等效为等壁厚壳体，可假设钢靶爆裂碎片具有相同初速v0。
基于Gurney公式，活性材料爆燃反应释放的总能量全部转换为金属壳体和爆轰产物的动能，则有
式中，me为进入侵孔内有效活性射流质量；Qv为单位活性材料质量含能量；mt为等效圆柱形钢壳质量（g）。
初速v0可表述为
根据侵孔通道与钢靶的几何关系，可得(https://www.chuimin.cn)
式中，D为钢靶初始直径；Da为侵孔平均直径；L表征活性射流侵孔深度。
将式（4.21）代入式（4.19），可得
由此，钢靶碎块数可表述为
式中，K是与钢靶材料相关的系数，可表述为
或
一般情况下，取ξ=160。
在大塑性变形条件下，σ（ε）可取为
式中，σ1和σ2为材料特征系数，常用材料的K值列于表4.5。
表4.5 常用材料的K值
由式（4.23）和式（4.24）可知，钢靶爆裂长度或碎块数除与钢靶材料和几何特征相关外，还显著受侵孔内活性聚能侵彻体有效质量和材料含能量的影响。
以90 mm口径活性药型罩聚能装药侵彻钢靶为例，理论计算所得钢靶碎块数与实验结果对比如图4.26所示。需要说明的是，实验所得钢靶碎块数是指侵孔通道部分钢靶碎块数与所形成的贯穿裂纹数之和。从图中可以看出，炸高分别为0.5 CD与1.0 CD时，计算所得钢靶碎块数与实验值较为吻合，但随着炸高的增加，二者偏差增大。其主要原因在于，一方面，理论分析中未考虑壳体变形能、爆轰产物内能及壳体周围介质吸收的能量，理论计算所得钢靶膨胀速度为理想极限速度，从而导致钢靶碎块平均尺寸减小，碎块数或裂纹数比实验值大；另一方面，随着炸高的增加，堆积在侵孔内的有效活性材料质量减少，导致爆燃反应产生强动载效应减弱，从而进一步导致实验结果与理论计算结果偏差增大。
图4.26 钢靶爆裂模型计算与实验结果对比
需要特别说明的是，钢靶碎裂行为理论模型存在一定的局限性。其主要原因在于，分析中假设活性聚能侵彻体在成形过程中完全是惰性的，该假设可能导致有效侵彻体质量偏大，钢靶碎块数量增多，尤其是当活性药型罩厚度较大时，理论分析误差更大。事实上，活性聚能侵彻体在成形阶段就会发生局部反应，且在侵彻过程中，活性聚能侵彻体能量释放也随侵彻时间线性变化。因此，假设活性聚能侵彻体在成形过程中完全是惰性的，会导致钢靶碎块数计算值偏大。
相关文章
- 详细阅读
-
MCB仿真分析：优化与探究详细阅读
在仿真中，采用动网格技术模拟动触头的运动过程，为了考虑栅片切割电弧后近极压降，模型中在栅片周围包含一层0.1mm厚度的鞘层，鞘层模型采用图8-22所示的非线性电阻。图8-64 MCB灭弧室内温度的分布a）0.05ms b）0.5ms c）3.5ms d）6.5ms图8-65 MCB电弧电压随时间变化的曲线......
2025-09-29
-
应急大数据存储模型优化方案详细阅读
应急大数据种类多，关系复杂。该混合时空数据模型将应急时空大数据抽象为数据集{时间，空间，事件}，如图2.10所示。其中时间轴T为UTC时间，空间轴X为与突发事件相关的空间基础数据，存储形式为CGCS2000坐标系下的大地坐标，事件轴E是突发事件的相关数据，主要包括致灾因子、承灾体、孕灾环境、抗灾体等数据。将X及E投影到时间轴，可视为在某一时间节点上的快照片段数据，表达为该时刻发生事件涉及的空间区域以及应急数据。......
2025-09-29
-
轴销寿命分析：优化方法探究详细阅读
图3-16 轴销寿命分布云图a）A3钢 b）调质45钢 c）调质40Cr由图3-16可见：1）轴销中间凸台部分的两侧寿命较短，是其薄弱环节，该结果与ADAMS软件的应力应变计算结果相符。2）轴销14698号节点的疲劳寿命最短，当选用材料为A3钢时，其疲劳寿命仅有4020次；当选用材料为调质45钢时，其疲劳寿命约为14000次，相比预期10000次机械寿命裕量较小；当选用材料为调质40Cr时，其疲劳寿命约为23000次，可以满足机械寿命10000次的要求，但是需要较高的材料成本。......
2025-09-29
-
非晶态有机固体电子输运模型优化详细阅读
非晶态分子固体的电子输运局限于分子个体中。电荷与感应极化共同作用的结果是产生了极化子。极化子模型具有严重的局限，不能始终为观察到的行为建立正确的模型。事实上，该模型未能反映出迁移率与电场和温度的关系，而非晶态分子固体的实验已表明这种关系的存在。由于电场的存在改变了位点的能量分布并降低了朝向该方向的平均能带隙，因此可以说非晶态有机固体的电荷迁移率与电场的关系十分密切。......
2025-09-29
-
优化载荷子输运模型的研究详细阅读
单极电荷的输运的数学公式已经被提出。目前，仍未出现同时考虑双极电流、输入受限输运和整体受限输运的统一模型。空穴输运在低能级上完成，所以空穴对因氧气等环境因素而产生的陷阱不敏感。相反，电子对距离较近的这类陷阱敏感并总是表现出弥散输运行为。该理论对OLED的输运描述而言是有价值的。同时，其他研究小组保留了SCLC理论的有效性，并且将迁移率与电场的关系包含在内，这种关系目前是强制性的。......
2025-09-29
-
活性聚能的毁伤机理优化方案详细阅读
图1.44活性药型罩聚能装药毁伤威力及性能要求抗过载能力。活性药型罩材料应具有一定的激活延时特性，在活性聚能侵彻体成形阶段尽量不发生反应，而侵入目标内适时发生爆燃反应，从而实现动能侵彻和爆燃化学能的双重高效毁伤机理。图1.46活性聚能侵彻体对本体功能型目标毁伤机理打击机库类目标，开孔大，后效毁伤强。......
2025-09-29
-
探究靶后化学能释放效应的影响因素详细阅读
为了研究靶板厚度对靶后化学能释放特性的影响规律，活性药型罩聚能装药在炸高为1.0 CD的条件下侵彻钢靶，钢靶厚度h分别为10 mm、20 mm、30 mm、40 mm、50 mm和60 mm。图3.25活性药型罩密度对靶后超压效应的影响表3.1炸高对活性聚能侵彻体靶后超压效应的影响在炸高为1.5 CD的条件下，活性药型罩密 度 为5.1 g/cm3、6.5 g/cm3和8.5 g/cm3所形成的活性聚能侵彻体均可穿透60 mm厚的钢靶，穿靶后在125 L密闭容器内产生的超压分别约为0.12......
2025-09-29
相关推荐