如何选择材料模型来提高非线性动力学数值模拟的精度？

2023-06-18 理论教育版权反馈

【摘要】：材料模型的选择是非线性动力学数值模拟中的另一个重要环节，在很大程度上决定了分析结果的精度。因为在绝热线上熵是常量，从而具备均匀初始条件的气体状态方程为2.强度模型强度模型是描述材料在冲击载荷作用下，屈服应力与应变、应变率、温度等参量之间复杂关系的数学模型。1）Johnson-Cook强度模型Johnson-Cook强度模型是一个能较好地反映材料应变率强化效应与温度软化效应的理想刚塑性强度模型。

材料模型的选择是非线性动力学数值模拟中的另一个重要环节，在很大程度上决定了分析结果的精度。在非线性动力学仿真过程中，材料运动由质量、动量和能量3个守恒方程来描述，求解这3个方程除了需要正确的初始条件和边界条件外，还需由材料模型来定义各变量之间的关系，包括状态方程、强度模型和失效模型3个方面。按材料性质的不同，失效模型又分为各向同性失效模型、各向异性失效模型和累积失效模型等几种。

1.状态方程

对于活性聚能侵彻体成形行为的数值模拟，常用的状态方程主要有3个，即Shock状态方程、JWL状态方程和理想气体状态方程。

1）Shock状态方程

Shock状态方程，即Mie-Gruneisen状态方程，是最常用的一种高压固体状态方程。Shock状态方程是在材料受压密度小于初始密度2倍的小压缩条件下建立的，一般只适用于描述固相材料高压状态，或者说只对遭遇速度在3 km/s以下的弹、靶碰撞作用过程有良好的适用性，而基本不适用于对有相变，特别是有气化现象发生的超高速碰撞作用行为的描述。也就是说，在图2.5所示p-v状态平面内，Shock状态方程一般只适用于对Ⅰ区状态的描述。在严格的热力学定义上，Mie-Gruneisen状态方程可表述为

pagenumber_ebook=75,pagenumber_book=58

图2.5　p-v状态平面分区

式中，p、v、e分别为固体材料的压力、比容及比内能；Γ（v）为Mie-Gruneisen系数，并具有以下性质（Mie-Gruneisen假设条件）：

式中，Γ0（v0）、v0为常态下的Mie-Gruneisen系数和比容。

通常，可借助实验测定固体材料压缩特性曲线，如冲击压缩Hugoniot曲线、等温压缩曲线、等熵压缩曲线等，来获得式（2.1）的积分形式Mie-Gruneisen状态方程。一般情况下，借助冲击波测量法先获得固体材料的冲击压缩Hugoniot曲线，进而得到积分形式的Mie-Gruneisen状态方程。

通过状态方程空间曲面（如p-v-e或p-v-T）上某种曲线在p-v状态平面上的投影，从冲击Hugoniot曲线上任选一参考点（pr（v），er（v）），并沿等容线对式（2.1）积分，得到积分形式Mie-Gruneisen状态方程：

由于参考点的压力和比内能已知，可建立压力、比容及内能间的关系。

2）JWL状态方程

JWL状态方程为高能炸药的爆轰方程，该方程可以很好地描述高能炸药爆轰及爆轰气体膨胀的过程，其表达式为

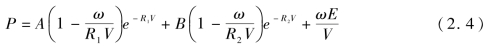
pagenumber_ebook=76,pagenumber_book=59

式中，p为压力；e为比内能；E为爆轰产物的内能；V为爆轰产物的相对体积；A、B、R1、R2和ω为与炸药有关的常数。

3）理想气体状态方程

最简单的状态方程形式即理想气体状态方程，该方程可从波义尔（Boyle）和吕萨克（Gay-Lussac）定律推导出来，表述为

式中，常数R可由通用气体常数R0和气体摩尔质量得到，即

理想气体内能仅是温度的函数，可表述为

式中，常数cv是质量定容热容。

熵的状态方程表述为

式中，S为比熵，绝热指数γ是一个常数。

因为在绝热线上熵是常量，从而具备均匀初始条件的气体状态方程为

2.强度模型

强度模型是描述材料在冲击载荷作用下，屈服应力与应变、应变率、温度等参量之间复杂关系的数学模型。在活性聚能侵彻体成形数值模拟中，常用材料强度模型有Johnson-Cook强度模型、Steinberg-Guinan强度模型等。

1）Johnson-Cook强度模型

Johnson-Cook强度模型是一个能较好地反映材料应变率强化效应与温度软化效应的理想刚塑性强度模型。该模型主要考虑温度和应变率对材料屈服应力的影响，而忽略了外部压力环境的影响。在Johnson-Cook模型中，屈服应力Y与应变ε、应变率ε˙和温度T之间的关系可表述为

pagenumber_ebook=77,pagenumber_book=60

式中，εp为等效塑性应变；A为准静态下材料屈服强度；B、n为应变硬化影响因子；C为应变率敏感系数；m为温度软化指数；相对温度TH=（T-T0）/（Tmelt-T0），其中，T为温度，T0为环境室温，Tmelt为材料熔点。

在式（2.10）中，右边第一项给出了ε˙ p=1.0/s和TH=0时，应力与应变之间的关系；第二和第三项分别描述了应变率和温度对屈服应力的影响。因此，Johnson-Cook模型可很好地描述材料应变、应变率及温度效应。

2）Steinberg-Guinan强度模型

Steinberg-Guinan强度模型的主要特点是，忽略了大应变率下（＞105 s-1）对强度影响较小的应变率效应，但考虑高温、高压环境对屈服应力和剪切模量的影响。大应变率条件下，剪切模量G和屈服应力Y之间的关系可表述为

pagenumber_ebook=77,pagenumber_book=60

其中

Y0［1+βε］n≤Ymax

式中，η=V0/V=ρ0/ρ，为材料压缩比；β、n为硬化功参数；ε为有效塑性应变；G′P、G′T分别为材料剪切模量的压力系数和温度系数，即剪切模量G对压力和温度的一阶偏导数；G0、Y0分别为材料在常温下的剪切模量和屈服应力；Ymax为材料屈服极限；其他参数的物理意义同上。

3.失效模型

失效模型为材料在受力作用下发生的失效行为提供了失效准则。按材料性质的不同，失效模型可分为各向同性失效（isotropic failure）、各向异性失效（directional failure）、累积失效（cumulative damage）等几种类型。

对于各向同性材料，如金属、非金属等绝大多数密实材料，由于在各个方向上的力学性能基本相同，不存在明显的方向性，当某些预先设定的参数达到临界值时即可认为失效，失效行为可以用各向同性失效模型来描述。

对于各向异性材料，如纤维增强复合材料、岩石、混凝土/钢筋混凝土介质等，由于在各个方向上的力学性能存在很大的不同，具有很强的方向性，失效行为需要由能准确判定材料沿各个不同方向发生失效的各向异性失效模型来描述，如Ortho模型。但由于这类模型往往比较复杂，有时也常采用累积失效模型近似描述。另外，由于各向异性失效模型无法准确跟踪欧拉网格单元主方向，一般只用于拉格朗日、ALE网格单元的计算分析。

累积失效模型主要用于描述某些宏观上无明显弹性力学行为的材料失效行为，如陶瓷、混凝土等材料在被压碎瞬间的失效行为。另外，对于材料所受拉应力低于其抗拉极限，但因作用时间足够长而导致材料发生碎裂的失效行为，也可用累积失效模型来描述。比较常用的有HJC、TCK等。

另外，还需要说明的是，对于活性聚能侵彻体成形行为及对目标侵彻行为也常通过SPH算法进行模拟，计算域通过填充SPH粒子实现，因此，使用SPH算法时，无须考虑材料失效行为及失效模型问题。

如何选择材料模型来提高非线性动力学数值模拟的精度？

相关推荐